Exponenta Banner
exponenta event banner

ncfsyn

Проектирование формирования петель методом Гловера-Макфарлейна

свернуть все на странице

Синтаксис

[K, CL, гамма, информация] = ncfsyn (G)
[K, CL, гамма, информация] = ncfsyn (G,W1)
[K, CL, гамма, информация] = ncfsyn (G,W1,W2)

Описание

ncfsyn реализует способ проектирования контроллеров, который использует комбинацию формирования контура и надежной стабилизации, как предложено в [1][2]-. Функция вычисляет нормированный контроллер K формирования контура коэффициента коприма Glover-McFarlane H∞ для установки G с весами W1 и W2 предкомпенсатора и посткомпенсатора. Функция предполагает положительную конфигурацию обратной связи на следующем рисунке.

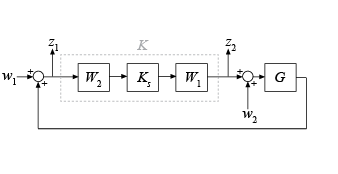
Чтобы задать отрицательную обратную связь, замените G на -G. Контроллер Ks стабилизирует семейство систем, задаваемых шариком неопределенности в нормированных копримовых факторах кумулятивной установки Gs = W2GW1. Конечный контроллер K, возвращенный ncfsyn получают в виде К = W1KsW2.

[K,CL,gamma,info] = ncfsyn(G) вычисляет контроллер формирования контуров с нормализованным коэффициентом коприма Glover-McFarlane H∞ K для завода G, с W1 = W2 = I. CL - система с замкнутым контуром от возмущений w1 и w2 к выходам z1 и z2. Функция также возвращает производительность H∞ gammaи структуру, содержащую дополнительную информацию о результате.

пример

[K,CL,gamma,info] = ncfsyn(G,W1) вычисляет контроллер с использованием веса предкомпенсатора, указанного в W1, с W2 = I.

[K,CL,gamma,info] = ncfsyn(G,W1,W2) вычисляет контроллер с использованием указанного веса предкомпенсатора W1 и вес после компенсатора W2.

Примеры

свернуть все

Открыть сценарий в реальном времени

Использовать ncfsyn разработать контроллер для следующей установки. 

G = tf([1 5],[1 2 10]);

Использовать функции взвешивания, позволяющие получить формованный завод W1*G*W2 с высоким коэффициентом усиления для ослабления возмущений ниже 0,1 рад/с и низким коэффициентом усиления для хорошей устойчивой стабильности выше около 5 рад/с. Для этого G, одного веса предварительного компенсатора достаточно. 

W1 = tf(1,[1 0]);
bodemag(W1*G)
grid

Figure contains an axes. The axes contains an object of type line. This object represents untitled1.

Вычислите контроллер.

[K,CL,gamma,info] = ncfsyn(G,W1);

Оптимальная стоимость gamma связан с нормированным запасом остойчивости системы на 1/gamma = ncfmargin(Gs,-Ks). (Знак «минус» необходим, поскольку ncfmargin предполагает цикл отрицательной обратной связи, в то время как ncfsyn вычисляет контроллер положительной обратной связи.) 

b = ncfmargin(info.Gs,-info.Ks);
[gamma 1/b]
ans = 1×2

    1.4508    1.4508

Сравните достигнутые и целевые формы цикла. 

sigma(G*K,G*W1)
legend('achieved','target')

Figure contains an axes. The axes contains 2 objects of type line. These objects represent achieved, target.

Входные аргументы

свернуть все

Установка, заданная как динамическая системная модель, например state-space (ss) модель. Если G является обобщенной моделью состояния-пространства с неопределенными или настраиваемыми блоками проектирования управления, то ncfsyn использует номинальное или текущее значение этих элементов. G должны иметь одинаковое количество входов и выходов.

Масса предкомпенсатора, указанная как:

  • Идентификационная матрица eye(N), где N - количество входов или выходов в G.

  • Модель LTI минимальной фазы SISO. В этом случае ncfsyn использует одинаковый вес для каждого канала шлейфа.

  • Модель минимально-фазового LTI MIMO с теми же размерами ввода/вывода, что и G.

Выберите веса предкомпенсатора и посткомпенсатора W1 и W2 так, чтобы коэффициент усиления формованной установки Gs = W2GW1 был достаточно высоким на частотах, где требуется хорошее затухание возмущений, и достаточно низким на частотах, где требуется хорошая надежная стабильность.

Вес посткомпенсатора, указанный как единичная матрица eye(N) или модель SISO или MIMO LTI. Соображения по определению W2 те же, что и для W1.

Выходные аргументы

свернуть все

H∞-optimal контроллер формирования петель, возвращаемый как state-space (ss) модель с теми же размерами ввода/вывода, что и G. Оптимальный контроллер K = W1KsW2. См. раздел Алгоритмы.

Оптимальная система с замкнутым контуром от возмущений w1 и w2 до выходов z1 и z2 возвращается в виде модели состояния-пространства. Замкнутая система задана:

[IK] (I − GK) − 1 [I, G].

H∞ производительность, достигаемая с помощью контроллера K, возвращается как положительное скалярное значение больше 1. Производительность H∞ - hinfnorm(CL). Оптимальный контроллер Ks таков, что график сингулярного значения формованного контура Ls = W2GW1Ks оптимально соответствует целевой форме контура Gs в пределах коэффициента gamma. Однако по численным причинам ncfsyn обычно возвращает контроллер с несколько большей H∞ производительностью, чем оптимальная. Для достижения оптимальной достижимой производительности см. info выходной аргумент.

gamma связан с нормированным запасом остойчивости системы на gamma = 1/ncfmargin(Gs,-Ks). Таким образом, gamma дает хорошую индикацию устойчивости к широкому классу неструктурированных вариаций установки со значениями в диапазоне 1 < gamma < 3 соответствует удовлетворительным пределам устойчивости для большинства типичных конструкций систем управления.

Дополнительная информация о синтезе контроллера, возвращенная в виде структуры, содержащей следующие поля.

  • gopt - Оптимальная производительность, достигаемая синтезом H∞ для фасонной установки. По числовым причинам ncfsyn обычно возвращает контроллер с немного большей производительностью H∞, который возвращается в gamma.

  • emax — nugap показатель надежности, emax = 1/gopt (см. gapmetric)

  • Gs - Фасонная установка Gs = W2GW1

  • Ks - Оптимальный контроллер для фасонной установки Gs. Конечный контроллер - K = W1KsW2. Дополнительные сведения см. в разделе Алгоритмы.

Совет

  • В то время как ncfmargin предполагает цикл отрицательной обратной связи, ncfsyn команда создает контроллер для цикла положительной обратной связи. Поэтому вычислять запас с помощью контроллера, разработанного с помощью ncfsyn, использовать [marg,freq] = ncfmargin(G,K,+1).

Алгоритмы

Возвращаемый контроллер K = W1KsW2, где Ks является оптимальным контроллером H∞, который минимизирует стоимость H∞

γ (Ks) = ‖ [IKs] (I − GsKs) − 1 [I, Gs] ‖ ∞= ‖ [IGs] (I − KsGs) − 1 [I, Ks] ‖ ∞.

Оптимальная производительность - это минимальные затраты

γ: = minKsγ (Ks).

Предположим, что Gs = NM-1, где N (j) * N (j) + M (j) * M (j) = I, является нормализованной параллельной факторизацией (NCF) взвешенной модели растения Gs. Тогда теория гарантирует, что система управления останется прочно стабильной при любых возмущениях, G˜s к Gs вида

G˜s= (N + Δ1) (M + Δ2) − 1

где Δ1, Δ2 - стабильная пара, удовлетворяющая

‖ [Δ1Δ2] ‖ ∞<MARG:=1γ.

Объект H∞-norm с замкнутым контуром имеет стандартную интерпретацию усиления сигнала. Наконец, можно показать, что контроллер, Ks, по существу не влияет на форму контура на частотах, где коэффициент усиления W2GW1 является либо высоким, либо низким, и гарантирует удовлетворительные пределы стабильности в частотной области пересечения коэффициента усиления. В настройках регулятора окончательный контроллер, который должен быть реализован, - K = W1KsW2.

Для получения дополнительной информации обратитесь к McFarlane и Glover [1] - [2].

Вопросы совместимости

развернуть все

Не рекомендуется начинать с R2020b

Ссылки

[1] Макфарлейн, округ Колумбия, и К. Гловер, надежная конструкция контроллера с использованием нормализованных описаний завода коприм-фактора, Springer Verlag, Lecture Notes in Control and Information Sciences, vol. 138, 1989.

[2] Макфарлейн, округ Колумбия, и К. Гловер, «A Loop Shaping Design Procedure using Synthesis», IEEE Transactions on Automatic Control, vol. 37, no. 6, pp. 759-769, June 1992.

[3] Винникомб, Г., «Измерение надежности систем обратной связи», кандидатская диссертация, инженерный факультет, Кембриджский университет, 1993.

[4] Чжоу, К. и Джей Си Дойл, Основы надежного контроля. Нью-Йорк: Прентис-Холл, 1998.

См. также

| | | |

Темы

Представлен до R2006a

Документация по инструментам надежного управления

Поддержка