Существует два типа вейвлет-анализа: непрерывный и мультиреолюционный. Тип вейвлет-анализа, наиболее подходящий для вашей работы, зависит от того, что вы хотите сделать с данными. В этом разделе рассматриваются 1-D данные, но можно применить те же принципы к 2-D данным. Сведения о том, как выполнять и интерпретировать каждый тип анализа, см. в разделе Практическое введение в непрерывный вейвлет-анализ и Практическое введение в анализ множественных решений.
Если целью является выполнение детального частотно-временного анализа, выберите непрерывное вейвлет-преобразование (CWT). С точки зрения реализации шкалы дискретизируются более точно в CWT, чем в дискретном вейвлет-преобразовании (DWT). Дополнительные сведения см. в разделе Непрерывные и дискретные вейвлет-преобразования.
CWT превосходит кратковременное преобразование Фурье (STFT) для сигналов, в которых мгновенная частота быстро растет. На следующем рисунке мгновенные частоты гиперболической чирпы строятся в виде пунктирных линий в спектрограмме и CWT-полученной скалограмме. Дополнительные сведения см. в разделах Частотно-временной анализ и Непрерывное вейвлет-преобразование.

CWT хорошо подходит для локализации переходных процессов в нестационарных сигналах. На следующем рисунке обратите внимание, насколько хорошо коэффициенты вейвлета согласуются с резкими изменениями, которые происходят в сигнале. Дополнительные сведения см. в разделе Практическое введение в непрерывный вейвлет-анализ.

Для получения непрерывного вейвлет-преобразования данных используйте cwt и cwtfilterbank. Обе функции поддерживают аналитические вейвлеты, перечисленные в следующей таблице. По умолчанию cwt и cwtfilterbank использовать обобщенное семейство вейвлетов Морзе. Это семейство определяется двумя параметрами. Можно изменять параметры для воссоздания многих часто используемых вейвлетов. На графиках временной области красная линия и синяя линия являются действительной и мнимой частями, соответственно, вейвлета. Контурные графики показывают вейвлет-разброс во времени и частоте. Дополнительные сведения см. в разделах Вейвлеты Морса и Обобщенные вейвлеты Морса и Аналитического Морлета.
| Небольшая волна | Особенности | Имя | Временная область | Частотно-временная область |
|---|---|---|---|---|
| Обобщенный вейвлет Морса | Изменение двух параметров для изменения разброса по времени и частоте | 'morse' (по умолчанию) |
|
|
| Аналитический Морлет (Габор) Вейвлет | Одинаковая дисперсия во времени и частоте | 'amor' |
|
|
| Ударный вейвлет | Более широкая дисперсия во времени, более узкая дисперсия в частоте | 'bump' |
|
|
Все вейвлеты в таблице являются аналитическими. Аналитические вейвлеты представляют собой вейвлеты с односторонними спектрами и имеют комплексные значения во временной области. Эти вейвлеты являются хорошим выбором для получения частотно-временного анализа с использованием CWT. Поскольку вейвлет-коэффициенты имеют комплексное значение, CWT предоставляет информацию о фазе. cwt и cwtfilterbank поддержка аналитических и антианалитических вейвлетов. Дополнительные сведения см. в разделе Анализ временных частот на основе CWT.
В анализе множественных решений (MRA) аппроксимация сигнала выполняется на постепенно более грубых шкалах при регистрации различий между аппроксимациями на последовательных шкалах. Аппроксимации и разности создаются с помощью дискретного вейвлет-преобразования (DWT) сигнала. DWT обеспечивает разреженное представление для многих естественных сигналов. Аппроксимации формируются путем сравнения сигнала с масштабированными и преобразованными копиями масштабной функции. Различия между последовательными масштабами, также известные как детали, регистрируются с использованием масштабированных и преобразованных копий вейвлета. На log2 , разница между последовательными шкалами всегда равна 1. В случае CWT различия между последовательными шкалами являются более тонкими.
При генерации MRA можно либо подпробовать (прореживать) приближение в 2 раза при каждом увеличении масштаба, либо. Каждый вариант предлагает преимущества и недостатки. При подсистеме получается то же количество вейвлет-коэффициентов, что и исходный сигнал. В прореженном DWT трансляции являются целыми кратными масштабу. Для недекимированного DWT трансляции являются целочисленными сдвигами. Недекимированный DWT обеспечивает избыточное представление исходных данных, но не такое избыточное, как CWT. Приложение влияет не только на выбор вейвлета, но и на используемую версию DWT.
Если сохранение энергии на этапе анализа важно, необходимо использовать ортогональный вейвлет. Ортогональное преобразование сохраняет энергию. Рассмотрите возможность использования ортогонального вейвлета с компактной поддержкой. Имейте в виду, что за исключением вейвлета Хаара ортогональные вейвлеты с компактной поддержкой не симметричны. Связанные фильтры имеют нелинейную фазу. В этой таблице перечислены поддерживаемые ортогональные вейвлеты. Посмотрите wavemngr('read') для всех имен семейств вейвлетов.
| Ортогональный вейвлет | Особенности | Имя | См. также | Представитель |
|---|---|---|---|---|
| Coiflet | Функция масштабирования и вейвлеты имеют одинаковое количество моментов исчезновения | 'coifN' для N = 1, 2,..., 5 | coifwavf, waveinfo |
|
| Daubechies | Нелинейная фаза; энергия сконцентрирована около начала их поддержки | 'dbN' для N = 1, 2,..., 45 | dbaux, waveinfo, Коэффициенты экстремального фазового вейвлета |
|
| Фежер-Коровкин | Фильтры, сконструированные для минимизации разницы между действительным масштабным фильтром и идеальным фильтром нижних частот sinc; особенно полезны при дискретных (прореженных и недекимированных) преобразованиях вейвлет-пакетов. | 'fkN' для N = 4, 6, 8, 14, 18, 22 | fejerkorovkin, waveinfo |
|
| Хаар | Симметричный; особый случай Daubechies; полезен для обнаружения кромок | 'haar' ('db1') | waveinfo |
|
| Symlet | Наименее асимметричный; почти линейная фаза | 'symN' для N = 2, 3,..., 45 | symaux, waveinfo, наименее асимметричный вейвлет и фаза |
|
Использовать waveinfo чтобы узнать больше об отдельных семействах вейвлетов. Например, waveinfo('db').
В зависимости от способа устранения искажений границ DWT может не экономить энергию на этапе анализа. Дополнительные сведения см. в разделе Граничные эффекты. Максимальное перекрытие дискретного вейвлет-преобразования modwt и максимальное перекрытие дискретного вейвлет-пакетного преобразования modwpt экономят энергию. Разложение вейвлет-пакета dwpt не экономит энергию.
Если вы хотите найти близко расположенные элементы, выберите вейвлеты с меньшей поддержкой, например haar, db2, или sym2. Поддержка вейвлета должна быть достаточно мала, чтобы разделить интересующие особенности. Вейвлеты с большей опорой имеют тенденцию к трудному обнаружению близко расположенных признаков. Использование вейвлетов с большой поддержкой может привести к коэффициентам, которые не различают отдельные особенности. На следующем рисунке верхний график показывает сигнал с шипами. На нижнем графике показаны детали MRA первого уровня максимального перекрытия DWT с использованием haar (толстые синие линии) и db6 (толстые красные линии) вейвлеты.
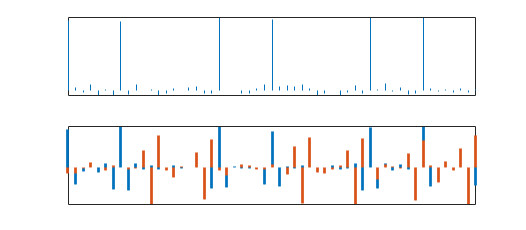
Если данные имеют мало разнесенных переходных процессов, можно использовать вейвлеты с большей поддержкой.
Если целью является проведение дисперсионного анализа, то для задачи подходит максимальное перекрытие дискретного вейвлет-преобразования (MODWT). MODWT является разновидностью стандартного DWT.
MODWT сохраняет энергию на стадии анализа.
Дисперсию разделов MODWT по масштабам. Примеры см. в разделах Вейвлет-анализ финансовых данных и Обнаружение точек изменения вейвлета.
Для MODWT требуется ортогональный вейвлет, такой как вейвлет Daubechies или Symlet.
MODWT является инвариантным преобразованием сдвига. Сдвиг входных данных сдвигает вейвлет-коэффициенты на идентичную величину. Прореженный DWT не является инвариантным сдвигом. Смещение входного сигнала изменяет коэффициенты и может перераспределять энергию по масштабам.
Посмотрите modwt, modwtmra, и modwtvar для получения дополнительной информации. См. также Сравнение MODWT и MODWTMRA.
Принимая прореженный DWT, wavedec, сигнала, использующего ортонормированное семейство вейвлетов, обеспечивает минимально избыточное представление сигнала. Отсутствует перекрытие вейвлетов внутри и поперек шкал. Число коэффициентов равно числу выборок сигнала. Минимально избыточные представления являются хорошим выбором для сжатия, когда требуется удалить элементы, которые не воспринимаются.
CWT сигнала обеспечивает сильно избыточное представление сигнала. Существует значительное перекрытие между вейвлетами внутри и поперек шкал. Кроме того, учитывая тонкую дискретизацию шкал, стоимость вычисления CWT и сохранения вейвлет-коэффициентов значительно больше, чем DWT. MODWT modwt также является избыточным преобразованием, но коэффициент избыточности обычно значительно меньше, чем CWT. Избыточность, как правило, усиливает характеристики сигнала и характеристики, которые необходимо изучить, например, разрывы частоты или другие переходные события.
Если ваша работа требует представления сигнала с минимальной избыточностью, используйте wavedec. Если для работы требуется избыточное представление, используйте modwt или modwpt.
Ортогональный вейвлет, такой как вейвлет Symlet или Daubechies, является хорошим выбором для затенения сигналов. Биоргональный вейвлет также может быть полезен для обработки изображения. Биоргональные вейвлет-фильтры имеют линейную фазу, которая очень важна для обработки изображения. Использование биорогонального вейвлета не будет вносить визуальных искажений в изображение.

Ортогональное преобразование не окрашивает белый шум. Если белый шум подается на вход ортогонального преобразования, то выходной сигнал является белым шумом. Выполнение DWT с биоргональным вейвлет-цветом белого шума.
Ортогональное преобразование сохраняет энергию.
sym4 вейвлет - вейвлет по умолчанию, используемый в wdenoise и вейвлет-сигнал Denoiser app. bior4.4 биортогональный вейвлет является вейвлетом по умолчанию в wdenoise2.
Если ваша работа связана со сжатием сигнала или изображения, рассмотрите возможность использования биорогонального вейвлета. В этой таблице перечислены поддерживаемые биорогональные вейвлеты с компактной поддержкой.
| Биортогональный вейвлет | Особенности | Имя | Представитель |
|---|---|---|---|
| Биортогональный сплайн | Компактная поддержка; симметричные фильтры; линейная фаза | 'biorNr.Nd' где Nr и Nd - количество моментов исчезновения для фильтров реконструкции и разложения соответственно; посмотрите waveinfo('bior') для поддерживаемых значений |
|
| Обратный биортогональный сплайн | Компактная поддержка; симметричные фильтры; линейная фаза | 'rbioNd.Nr' где Nr и Nd - количество моментов исчезновения для фильтров реконструкции и разложения соответственно; посмотрите waveinfo('rbio') для поддерживаемых значений |
|
Наличие двух масштабирующих функциональных пар - вейвлет, одной пары для анализа и другой для синтеза, полезно для сжатия.
Биортогональные вейвлет-фильтры симметричны и имеют линейную фазу. (См. раздел Наименьший асимметричный вейвлет и фаза.)
Вейвлеты, используемые для анализа, могут иметь много моментов исчезновения. Вейвлет с N моментами исчезновения ортогональен многочленам степени N-1. Использование вейвлета с множеством исчезающих моментов приводит к меньшему количеству значимых вейвлет-коэффициентов. Улучшено сжатие.
Двойные вейвлеты, используемые для синтеза, могут иметь лучшую регулярность. Восстановленный сигнал является более плавным.
Использование фильтра анализа с меньшим количеством моментов исчезновения, чем фильтр синтеза, может отрицательно повлиять на сжатие. Пример см. в разделе Реконструкция изображения с помощью биорогональных вейвлетов.
При использовании биорогональных вейвлетов энергия не сохраняется на этапе анализа. Дополнительные сведения см. в разделе Банки ортогональных и биортогенных фильтров.
Вейвлеты имеют свойства, управляющие их поведением. В зависимости от того, что вы хотите сделать, некоторые свойства могут быть более важными.
Если вейвлет ортогональен, вейвлет-преобразование сохраняет энергию. За исключением вейвлета Хаара, никакой ортогональный вейвлет с компактной поддержкой не симметричен. Связанный фильтр имеет нелинейную фазу.
Вейвлет с N исчезающими моментами ортогональен многочленам степени N − 1. Пример см. в разделе Вейвлеты и исчезающие моменты. Количество исчезающих моментов и колебание импульса имеют свободную зависимость. По мере роста числа исчезающих моментов, чем больше колеблется вейвлет.
Количество исчезающих моментов также влияет на поддержку вейвлета. Даубехии доказали, что вейвлет с N исчезающими моментами должен иметь опору по меньшей мере длиной 2N-1.
Имена многих вейвлетов получаются из числа исчезающих моментов. Например, db6 является вейвлет Daubechies с шестью исчезающими моментами, и sym3 является Symlet с тремя исчезающими моментами. Для вейвлетов койфлета, coif3 это койфлет с шестью исчезающими моментами. Для вейвлетов Фейера-Коровкина, fk8 - вейвлет Фейера - Коровкина с фильтром длиной 8. Биортогональные имена вейвлетов получаются из числа исчезающих моментов, которые имеют вейвлет анализа и вейвлет синтеза. Например, bior3.5 является биортогенным вейвлетом с тремя исчезающими моментами в вейвлете синтеза и пятью исчезающими моментами в вейвлете анализа. Дополнительные сведения см. в разделе waveinfo и wavemngr.
Если число исчезающих моментов N равно 1, 2 или 3, то dbN и symN идентичны.
Регулярность связана с тем, сколько непрерывных производных имеет функция. Интуитивно регулярность можно считать мерой гладкости. Для обнаружения резкого изменения данных вейвлет должен быть достаточно регулярным. Чтобы вейвлет имел N непрерывных производных, вейвлет должен иметь по меньшей мере N + 1 исчезающих моментов. Пример см. в разделе Обнаружение разрывов и точек разбивки. Если ваши данные относительно гладкие с несколькими переходными процессами, более регулярный вейвлет может быть лучше подходит для вашей работы.
[1] Даубехии, Ингрид. Десять лекций по вейвлетам. Общество промышленной и прикладной математики, 1992 год.
cwt | cwtfilterbank | dwtfilterbank | wavedec | wavedec2 | waveinfo | wavemngr | wdenoise | wdenoise2