estimate

Оцените апостериорное распределение параметров модели Байесовской векторной авторегрессии (VAR)

Синтаксис

PosteriorMdl = estimate(PriorMdl,Y)

PosteriorMdl = estimate(PriorMdl,Y,Name,Value)

[PosteriorMdl,Summary]
= estimate(___)

Описание

пример

PosteriorMdl = estimate(PriorMdl,Y) возвращает модель Bayesian VAR (p) PosteriorMdl это характеризует совместные следующие распределения коэффициентов Λ и инновационная ковариационная матрица Σ. PriorMdl задает предварительное распределение параметров и структуры модели VAR в соединениях. Y - многомерные данные отклика. PriorMdl и PosteriorMdl возможно, не совпадает с типом объекта.

NaNs в данных указывают отсутствующие значения, которые estimate удаляет при помощи спискового удаления.

пример

PosteriorMdl = estimate(PriorMdl,Y,Name,Value) задает дополнительные опции, используя один или несколько аргументы пары "имя-значение". Например, можно задать предварительный образец данных для инициализации модели VAR с помощью 'Y0' аргумент пары "имя-значение".

пример

[PosteriorMdl,Summary] = estimate(___) также возвращает сводные данные оценок апостериорного распределения Summary, использование любой комбинации входных аргументов в предыдущих синтаксисах.

Примеры

свернуть все

Оценка апостериорного распределения

Открыть Live Script

Рассмотрим 3-D модель VAR (4) для инфляции в США (INFL), безработица (UNRATE), и федеральные фонды (FEDFUNDS) ставки.

$[\begin{array}{llllllllllllllllllll} {INFL}_{t} \\ {UNRATE}_{t} \\ {FEDFUNDS}_{t} \end{array}] = c + \sum_{j = 1}^{4} Φ_{j} [\begin{array}{llllllllllllllllllll} {INFL}_{t - j} \\ {UNRATE}_{t - j} \\ {FEDFUNDS}_{t - j} \end{array}] + [\begin{array}{cccccccccccccccccccc} ε_{1, t} \\ ε_{2, t} \\ ε_{3, t} \end{array}] .$

Для всех $t$ , $ε_{t}$ - серия независимых 3-D нормальных инноваций со средним значением 0 и ковариацией $Σ$ . Примите, что соединение предшествующего распределения параметров модели VAR $({[Φ_{1}, . . ., Φ_{4}, c]}^{'}, Σ)$ является диффузным.

Загрузка и предварительная обработка данных

Загрузите набор макроэкономических данных США. Вычислите уровень инфляции. Постройте график всех ответных рядов.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

figure
plot(DataTable.Time,DataTable{:,seriesnames})
legend(seriesnames)

Figure contains an axes. The axes contains 3 objects of type line. These objects represent INFL, UNRATE, FEDFUNDS.

Стабилизировать показатели безработицы и федеральных средств путем применения первого различия к каждой серии.

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);

Удалите все отсутствующие значения из данных.

rmDataTable = rmmissing(DataTable);

Создайте предыдущую модель

Создайте диффузную модель Bayesian VAR (4) для трех рядов откликов. Задайте имена переменных отклика.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'SeriesNames',seriesnames)

PriorMdl = 
  diffusebvarm with properties:

        Description: "3-Dimensional VAR(4) Model"
          NumSeries: 3
                  P: 4
        SeriesNames: ["INFL"    "DUNRATE"    "DFEDFUNDS"]
    IncludeConstant: 1
       IncludeTrend: 0
      NumPredictors: 0
                 AR: {[3x3 double]  [3x3 double]  [3x3 double]  [3x3 double]}
           Constant: [3x1 double]
              Trend: [3x0 double]
               Beta: [3x0 double]
         Covariance: [3x3 double]

PriorMdl является diffusebvarm объект модели.

Оценка апостериорного распределения

Оцените апостериорное распределение путем передачи предыдущей модели и целого ряда данных в estimate.

PosteriorMdl = estimate(PriorMdl,rmDataTable{:,seriesnames})

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
             |   Mean     Std  
-------------------------------
 Constant(1) |  0.1007  0.0832 
 Constant(2) | -0.0499  0.0450 
 Constant(3) | -0.4221  0.1781 
 AR{1}(1,1)  |  0.1241  0.0762 
 AR{1}(2,1)  | -0.0219  0.0413 
 AR{1}(3,1)  | -0.1586  0.1632 
 AR{1}(1,2)  | -0.4809  0.1536 
 AR{1}(2,2)  |  0.4716  0.0831 
 AR{1}(3,2)  | -1.4368  0.3287 
 AR{1}(1,3)  |  0.1005  0.0390 
 AR{1}(2,3)  |  0.0391  0.0211 
 AR{1}(3,3)  | -0.2905  0.0835 
 AR{2}(1,1)  |  0.3236  0.0868 
 AR{2}(2,1)  |  0.0913  0.0469 
 AR{2}(3,1)  |  0.3403  0.1857 
 AR{2}(1,2)  | -0.0503  0.1647 
 AR{2}(2,2)  |  0.2414  0.0891 
 AR{2}(3,2)  | -0.2968  0.3526 
 AR{2}(1,3)  |  0.0450  0.0413 
 AR{2}(2,3)  |  0.0536  0.0223 
 AR{2}(3,3)  | -0.3117  0.0883 
 AR{3}(1,1)  |  0.4272  0.0860 
 AR{3}(2,1)  | -0.0389  0.0465 
 AR{3}(3,1)  |  0.2848  0.1841 
 AR{3}(1,2)  |  0.2738  0.1620 
 AR{3}(2,2)  |  0.0552  0.0876 
 AR{3}(3,2)  | -0.7401  0.3466 
 AR{3}(1,3)  |  0.0523  0.0428 
 AR{3}(2,3)  |  0.0008  0.0232 
 AR{3}(3,3)  |  0.0028  0.0917 
 AR{4}(1,1)  |  0.0167  0.0901 
 AR{4}(2,1)  |  0.0285  0.0488 
 AR{4}(3,1)  | -0.0690  0.1928 
 AR{4}(1,2)  | -0.1830  0.1520 
 AR{4}(2,2)  | -0.1795  0.0822 
 AR{4}(3,2)  |  0.1494  0.3253 
 AR{4}(1,3)  |  0.0067  0.0395 
 AR{4}(2,3)  |  0.0088  0.0214 
 AR{4}(3,3)  | -0.1372  0.0845 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

PosteriorMdl = 
  conjugatebvarm with properties:

        Description: "3-Dimensional VAR(4) Model"
          NumSeries: 3
                  P: 4
        SeriesNames: ["INFL"    "DUNRATE"    "DFEDFUNDS"]
    IncludeConstant: 1
       IncludeTrend: 0
      NumPredictors: 0
                 Mu: [39x1 double]
                  V: [13x13 double]
              Omega: [3x3 double]
                DoF: 184
                 AR: {[3x3 double]  [3x3 double]  [3x3 double]  [3x3 double]}
           Constant: [3x1 double]
              Trend: [3x0 double]
               Beta: [3x0 double]
         Covariance: [3x3 double]

PosteriorMdl является conjugatebvarm объект модели; апостериор аналитически прослеживается. В командной строке отображаются апостериорные средства (Mean) и стандартные отклонения (Std) всех коэффициентов и ковариационной матрицы инноваций. Строка AR{k}(i,j) содержит апостериорные оценки $ϕ_{k, ij}$ , задержка k Переменный коэффициент переменной AR j в уравнении отклика i. По умолчанию estimate использует первые четыре наблюдения в качестве предварительной выборки для инициализации модели.

Отобразите апостериорные средства матриц коэффициентов AR с помощью записи через точку.

AR1 = PosteriorMdl.AR{1}

AR1 = 3×3

    0.1241   -0.4809    0.1005
   -0.0219    0.4716    0.0391
   -0.1586   -1.4368   -0.2905

AR2 = PosteriorMdl.AR{2}

AR2 = 3×3

    0.3236   -0.0503    0.0450
    0.0913    0.2414    0.0536
    0.3403   -0.2968   -0.3117

AR3 = PosteriorMdl.AR{3}

AR3 = 3×3

    0.4272    0.2738    0.0523
   -0.0389    0.0552    0.0008
    0.2848   -0.7401    0.0028

AR4 = PosteriorMdl.AR{4}

AR4 = 3×3

    0.0167   -0.1830    0.0067
    0.0285   -0.1795    0.0088
   -0.0690    0.1494   -0.1372

Задайте данные предварительного образца

Открыть Live Script

Рассмотрим 3-D модель VAR (4) оценки апостериорного распределения. В этом случае подгонка модели к данным начиная с 1970 года.

Загрузка и предварительная обработка данных

Загрузите набор макроэкономических данных США. Рассчитать уровень инфляции, стабилизировать ставки по безработице и федеральным фондам и удалить отсутствующие значения.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте предыдущую модель

Создайте диффузную модель Bayesian VAR (4) для трех рядов откликов. Задайте имена переменных отклика.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = diffusebvarm(numseries,numlags,'SeriesNames',seriesnames);

Основа времени разбиения для подвыборок

Модель VAR (4) требует p = 4 предварительных наблюдений, чтобы инициализировать AR- компонента для оценки. Задайте наборы индексов, соответствующие необходимым предварительным выборкам и оценочным выборкам.

idxpre = rmDataTable.Time < datetime('1970','InputFormat','yyyy');  % Presample indices
idxest = ~idxpre;                                                   % Estimation sample indices
T = sum(idxest)

T = 157

Эффективный размер выборки 157 наблюдения.

Оценка апостериорного распределения

Оцените апостериорное распределение. Задайте только необходимые наблюдения предварительного образца при помощи 'Y0' аргумент пары "имя-значение".

Y0 = rmDataTable{find(idxpre,PriorMdl.P,'last'),seriesnames};
PosteriorMdl = estimate(PriorMdl,rmDataTable{idxest,seriesnames},...
    'Y0',Y0);

Bayesian VAR under diffuse priors
Effective Sample Size:          157
Number of equations:            3
Number of estimated Parameters: 39
             |   Mean     Std  
-------------------------------
 Constant(1) |  0.1431  0.1134 
 Constant(2) | -0.0132  0.0588 
 Constant(3) | -0.6864  0.2418 
 AR{1}(1,1)  |  0.1314  0.0869 
 AR{1}(2,1)  | -0.0187  0.0450 
 AR{1}(3,1)  | -0.2009  0.1854 
 AR{1}(1,2)  | -0.5009  0.1834 
 AR{1}(2,2)  |  0.4881  0.0950 
 AR{1}(3,2)  | -1.6913  0.3912 
 AR{1}(1,3)  |  0.1089  0.0446 
 AR{1}(2,3)  |  0.0555  0.0231 
 AR{1}(3,3)  | -0.3588  0.0951 
 AR{2}(1,1)  |  0.2942  0.1012 
 AR{2}(2,1)  |  0.0786  0.0524 
 AR{2}(3,1)  |  0.3767  0.2157 
 AR{2}(1,2)  |  0.0208  0.2042 
 AR{2}(2,2)  |  0.3238  0.1058 
 AR{2}(3,2)  | -0.4530  0.4354 
 AR{2}(1,3)  |  0.0634  0.0487 
 AR{2}(2,3)  |  0.0747  0.0252 
 AR{2}(3,3)  | -0.3594  0.1038 
 AR{3}(1,1)  |  0.4503  0.1002 
 AR{3}(2,1)  | -0.0388  0.0519 
 AR{3}(3,1)  |  0.3580  0.2136 
 AR{3}(1,2)  |  0.3119  0.2008 
 AR{3}(2,2)  |  0.0966  0.1040 
 AR{3}(3,2)  | -0.8212  0.4282 
 AR{3}(1,3)  |  0.0659  0.0502 
 AR{3}(2,3)  |  0.0155  0.0260 
 AR{3}(3,3)  | -0.0269  0.1070 
 AR{4}(1,1)  | -0.0141  0.1046 
 AR{4}(2,1)  |  0.0105  0.0542 
 AR{4}(3,1)  |  0.0263  0.2231 
 AR{4}(1,2)  | -0.2274  0.1875 
 AR{4}(2,2)  | -0.1734  0.0972 
 AR{4}(3,2)  |  0.1328  0.3999 
 AR{4}(1,3)  |  0.0028  0.0456 
 AR{4}(2,3)  |  0.0094  0.0236 
 AR{4}(3,3)  | -0.1487  0.0973 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3597   -0.0333     0.1987  
           | (0.0433)  (0.0161)   (0.0672) 
 DUNRATE   | -0.0333    0.0966    -0.1647  
           | (0.0161)  (0.0116)   (0.0365) 
 DFEDFUNDS |  0.1987   -0.1647     1.6355  
           | (0.0672)  (0.0365)   (0.1969)

Просмотр и возврат сводных данных оценок

Открыть Live Script

Рассмотрим 3-D модель VAR (4) оценки апостериорного распределения.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте диффузную модель Bayesian VAR (4) для трех рядов откликов. Задайте имена переменных отклика.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = diffusebvarm(numseries,numlags,'SeriesNames',seriesnames);

Можно отобразить выход оценки тремя способами или выключить отображение. Сравните типы отображения.

estimate(PriorMdl,rmDataTable{:,seriesnames}); % 'table', the default

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
             |   Mean     Std  
-------------------------------
 Constant(1) |  0.1007  0.0832 
 Constant(2) | -0.0499  0.0450 
 Constant(3) | -0.4221  0.1781 
 AR{1}(1,1)  |  0.1241  0.0762 
 AR{1}(2,1)  | -0.0219  0.0413 
 AR{1}(3,1)  | -0.1586  0.1632 
 AR{1}(1,2)  | -0.4809  0.1536 
 AR{1}(2,2)  |  0.4716  0.0831 
 AR{1}(3,2)  | -1.4368  0.3287 
 AR{1}(1,3)  |  0.1005  0.0390 
 AR{1}(2,3)  |  0.0391  0.0211 
 AR{1}(3,3)  | -0.2905  0.0835 
 AR{2}(1,1)  |  0.3236  0.0868 
 AR{2}(2,1)  |  0.0913  0.0469 
 AR{2}(3,1)  |  0.3403  0.1857 
 AR{2}(1,2)  | -0.0503  0.1647 
 AR{2}(2,2)  |  0.2414  0.0891 
 AR{2}(3,2)  | -0.2968  0.3526 
 AR{2}(1,3)  |  0.0450  0.0413 
 AR{2}(2,3)  |  0.0536  0.0223 
 AR{2}(3,3)  | -0.3117  0.0883 
 AR{3}(1,1)  |  0.4272  0.0860 
 AR{3}(2,1)  | -0.0389  0.0465 
 AR{3}(3,1)  |  0.2848  0.1841 
 AR{3}(1,2)  |  0.2738  0.1620 
 AR{3}(2,2)  |  0.0552  0.0876 
 AR{3}(3,2)  | -0.7401  0.3466 
 AR{3}(1,3)  |  0.0523  0.0428 
 AR{3}(2,3)  |  0.0008  0.0232 
 AR{3}(3,3)  |  0.0028  0.0917 
 AR{4}(1,1)  |  0.0167  0.0901 
 AR{4}(2,1)  |  0.0285  0.0488 
 AR{4}(3,1)  | -0.0690  0.1928 
 AR{4}(1,2)  | -0.1830  0.1520 
 AR{4}(2,2)  | -0.1795  0.0822 
 AR{4}(3,2)  |  0.1494  0.3253 
 AR{4}(1,3)  |  0.0067  0.0395 
 AR{4}(2,3)  |  0.0088  0.0214 
 AR{4}(3,3)  | -0.1372  0.0845 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

estimate(PriorMdl,rmDataTable{:,seriesnames},...
    'Display','equation');

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
                                                                                 VAR Equations                                                                                
           | INFL(-1)  DUNRATE(-1)  DFEDFUNDS(-1)  INFL(-2)  DUNRATE(-2)  DFEDFUNDS(-2)  INFL(-3)  DUNRATE(-3)  DFEDFUNDS(-3)  INFL(-4)  DUNRATE(-4)  DFEDFUNDS(-4)  Constant 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 INFL      |  0.1241     -0.4809        0.1005      0.3236     -0.0503        0.0450      0.4272      0.2738        0.0523      0.0167     -0.1830        0.0067      0.1007  
           | (0.0762)    (0.1536)      (0.0390)    (0.0868)    (0.1647)      (0.0413)    (0.0860)    (0.1620)      (0.0428)    (0.0901)    (0.1520)      (0.0395)    (0.0832) 
 DUNRATE   | -0.0219      0.4716        0.0391      0.0913      0.2414        0.0536     -0.0389      0.0552        0.0008      0.0285     -0.1795        0.0088     -0.0499  
           | (0.0413)    (0.0831)      (0.0211)    (0.0469)    (0.0891)      (0.0223)    (0.0465)    (0.0876)      (0.0232)    (0.0488)    (0.0822)      (0.0214)    (0.0450) 
 DFEDFUNDS | -0.1586     -1.4368       -0.2905      0.3403     -0.2968       -0.3117      0.2848     -0.7401        0.0028     -0.0690      0.1494       -0.1372     -0.4221  
           | (0.1632)    (0.3287)      (0.0835)    (0.1857)    (0.3526)      (0.0883)    (0.1841)    (0.3466)      (0.0917)    (0.1928)    (0.3253)      (0.0845)    (0.1781) 
 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

estimate(PriorMdl,rmDataTable{:,seriesnames},...
    'Display','matrix');

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
          VAR Coefficient Matrix of Lag 1         
           | INFL(-1)  DUNRATE(-1)  DFEDFUNDS(-1) 
--------------------------------------------------
 INFL      |  0.1241     -0.4809        0.1005    
           | (0.0762)    (0.1536)      (0.0390)   
 DUNRATE   | -0.0219      0.4716        0.0391    
           | (0.0413)    (0.0831)      (0.0211)   
 DFEDFUNDS | -0.1586     -1.4368       -0.2905    
           | (0.1632)    (0.3287)      (0.0835)   
 
          VAR Coefficient Matrix of Lag 2         
           | INFL(-2)  DUNRATE(-2)  DFEDFUNDS(-2) 
--------------------------------------------------
 INFL      |  0.3236     -0.0503        0.0450    
           | (0.0868)    (0.1647)      (0.0413)   
 DUNRATE   |  0.0913      0.2414        0.0536    
           | (0.0469)    (0.0891)      (0.0223)   
 DFEDFUNDS |  0.3403     -0.2968       -0.3117    
           | (0.1857)    (0.3526)      (0.0883)   
 
          VAR Coefficient Matrix of Lag 3         
           | INFL(-3)  DUNRATE(-3)  DFEDFUNDS(-3) 
--------------------------------------------------
 INFL      |  0.4272      0.2738        0.0523    
           | (0.0860)    (0.1620)      (0.0428)   
 DUNRATE   | -0.0389      0.0552        0.0008    
           | (0.0465)    (0.0876)      (0.0232)   
 DFEDFUNDS |  0.2848     -0.7401        0.0028    
           | (0.1841)    (0.3466)      (0.0917)   
 
          VAR Coefficient Matrix of Lag 4         
           | INFL(-4)  DUNRATE(-4)  DFEDFUNDS(-4) 
--------------------------------------------------
 INFL      |  0.0167     -0.1830        0.0067    
           | (0.0901)    (0.1520)      (0.0395)   
 DUNRATE   |  0.0285     -0.1795        0.0088    
           | (0.0488)    (0.0822)      (0.0214)   
 DFEDFUNDS | -0.0690      0.1494       -0.1372    
           | (0.1928)    (0.3253)      (0.0845)   
 
     Constant Term    
 INFL      |  0.1007  
           | (0.0832) 
 DUNRATE   | -0.0499  
           |  0.0450  
 DFEDFUNDS | -0.4221  
           |  0.1781  
 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

Возвращает сводные данные оценок, которая является структурой, содержащей ту же информацию независимо от типа отображения.

[PosteriorMdl,Summary] = estimate(PriorMdl,rmDataTable{:,seriesnames});

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
             |   Mean     Std  
-------------------------------
 Constant(1) |  0.1007  0.0832 
 Constant(2) | -0.0499  0.0450 
 Constant(3) | -0.4221  0.1781 
 AR{1}(1,1)  |  0.1241  0.0762 
 AR{1}(2,1)  | -0.0219  0.0413 
 AR{1}(3,1)  | -0.1586  0.1632 
 AR{1}(1,2)  | -0.4809  0.1536 
 AR{1}(2,2)  |  0.4716  0.0831 
 AR{1}(3,2)  | -1.4368  0.3287 
 AR{1}(1,3)  |  0.1005  0.0390 
 AR{1}(2,3)  |  0.0391  0.0211 
 AR{1}(3,3)  | -0.2905  0.0835 
 AR{2}(1,1)  |  0.3236  0.0868 
 AR{2}(2,1)  |  0.0913  0.0469 
 AR{2}(3,1)  |  0.3403  0.1857 
 AR{2}(1,2)  | -0.0503  0.1647 
 AR{2}(2,2)  |  0.2414  0.0891 
 AR{2}(3,2)  | -0.2968  0.3526 
 AR{2}(1,3)  |  0.0450  0.0413 
 AR{2}(2,3)  |  0.0536  0.0223 
 AR{2}(3,3)  | -0.3117  0.0883 
 AR{3}(1,1)  |  0.4272  0.0860 
 AR{3}(2,1)  | -0.0389  0.0465 
 AR{3}(3,1)  |  0.2848  0.1841 
 AR{3}(1,2)  |  0.2738  0.1620 
 AR{3}(2,2)  |  0.0552  0.0876 
 AR{3}(3,2)  | -0.7401  0.3466 
 AR{3}(1,3)  |  0.0523  0.0428 
 AR{3}(2,3)  |  0.0008  0.0232 
 AR{3}(3,3)  |  0.0028  0.0917 
 AR{4}(1,1)  |  0.0167  0.0901 
 AR{4}(2,1)  |  0.0285  0.0488 
 AR{4}(3,1)  | -0.0690  0.1928 
 AR{4}(1,2)  | -0.1830  0.1520 
 AR{4}(2,2)  | -0.1795  0.0822 
 AR{4}(3,2)  |  0.1494  0.3253 
 AR{4}(1,3)  |  0.0067  0.0395 
 AR{4}(2,3)  |  0.0088  0.0214 
 AR{4}(3,3)  | -0.1372  0.0845 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

Summary

Summary = struct with fields:
               Description: "3-Dimensional VAR(4) Model"
    NumEstimatedParameters: 39
                     Table: [39x2 table]
                  CoeffMap: [39x1 string]
                 CoeffMean: [39x1 double]
                  CoeffStd: [39x1 double]
                 SigmaMean: [3x3 double]
                  SigmaStd: [3x3 double]

The CoeffMap поле содержит список имен коэффициентов. Порядок имен соответствует порядку всех входных и выходных входов вектора коэффициентов. Отобразите CoeffMap.

Summary.CoeffMap

ans = 39x1 string
    "AR{1}(1,1)"
    "AR{1}(1,2)"
    "AR{1}(1,3)"
    "AR{2}(1,1)"
    "AR{2}(1,2)"
    "AR{2}(1,3)"
    "AR{3}(1,1)"
    "AR{3}(1,2)"
    "AR{3}(1,3)"
    "AR{4}(1,1)"
    "AR{4}(1,2)"
    "AR{4}(1,3)"
    "Constant(1)"
    "AR{1}(2,1)"
    "AR{1}(2,2)"
    "AR{1}(2,3)"
    "AR{2}(2,1)"
    "AR{2}(2,2)"
    "AR{2}(2,3)"
    "AR{3}(2,1)"
    "AR{3}(2,2)"
    "AR{3}(2,3)"
    "AR{4}(2,1)"
    "AR{4}(2,2)"
    "AR{4}(2,3)"
    "Constant(2)"
    "AR{1}(3,1)"
    "AR{1}(3,2)"
    "AR{1}(3,3)"
    "AR{2}(3,1)"
      ⋮

Оценка апостериорной функции с разреженными коэффициентами

Открыть Live Script

Рассмотрим 3-D модель VAR (4) оценки апостериорного распределения В этом примере создайте нормальную сопряженную предшествующую модель с матрицей фиксированных коэффициентов вместо диффузной модели. Модель содержит 39 коэффициентов. Для разреженности коэффициентов в апостериорной функции примените метод регуляризации Миннесоты во время оценки.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте нормальную сопряженную предшествующую модель Bayesian VAR (4) для трех рядов откликов. Задайте имена переменных отклика и установите ковариационную матрицу инноваций

$Σ = [\begin{array}{cccccccccccccccccccc} 10^{- 5} & 0 & 10^{- 4} \\ 0 & 0.1 & - 0.2 \\ 10^{- 4} & - 0.2 & 1.6 \end{array}] .$

Согласно методу регуляризации Миннесоты, укажите следующее:

Каждый ответ является моделью AR (1), в среднем с коэффициентом задержки 1 0,75.
Предыдущие коэффициенты автозадания имеют отклонение 100. Эта большая настройка отклонения позволяет данным влиять на апостериор больше, чем на предыдущий.
Предыдущие коэффициенты перекрестной задержки имеют отклонение 0,01. Эта настройка малых отклонений затягивает коэффициенты перекрестной задержки до нуля во время оценки.
Ковариации предшествующего коэффициента распадаются с увеличением задержки со скоростью 10 (то есть более низкие лаги важнее, чем более высокие лаги).

numseries = numel(seriesnames);
numlags = 4;
Sigma = [10e-5 0 10e-4; 0 0.1 -0.2; 10e-4 -0.2 1.6]; 

PriorMdl = bayesvarm(numseries,numlags,'Model','normal','SeriesNames',seriesnames,...
    'Center',0.75,'SelfLag',100,'CrossLag',0.01,'Decay',10,...
    'Sigma',Sigma);

Оцените апостериорное распределение и отобразите уравнения апостериорной реакции.

PosteriorMdl = estimate(PriorMdl,rmDataTable{:,seriesnames},'Display','equation');

Bayesian VAR under normal priors and fixed Sigma
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
                                                                                 VAR Equations                                                                                
           | INFL(-1)  DUNRATE(-1)  DFEDFUNDS(-1)  INFL(-2)  DUNRATE(-2)  DFEDFUNDS(-2)  INFL(-3)  DUNRATE(-3)  DFEDFUNDS(-3)  INFL(-4)  DUNRATE(-4)  DFEDFUNDS(-4)  Constant 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 INFL      |  0.1234     -0.4373        0.1050      0.3343     -0.0342        0.0308      0.4441      0.0031        0.0090      0.0083     -0.0003        0.0003      0.0820  
           | (0.0014)    (0.0027)      (0.0007)    (0.0015)    (0.0021)      (0.0006)    (0.0015)    (0.0004)      (0.0003)    (0.0015)    (0.0001)      (0.0001)    (0.0014) 
 DUNRATE   |  0.0521      0.3636        0.0125      0.0012      0.1720        0.0009      0.0000     -0.0741       -0.0000      0.0000      0.0007       -0.0000     -0.0413  
           | (0.0252)    (0.0723)      (0.0191)    (0.0031)    (0.0666)      (0.0031)    (0.0004)    (0.0348)      (0.0004)    (0.0001)    (0.0096)      (0.0001)    (0.0339) 
 DFEDFUNDS | -0.0105     -0.1394       -0.1368      0.0002     -0.0000       -0.1227      0.0000     -0.0000        0.0085     -0.0000      0.0000       -0.0041     -0.0113  
           | (0.0749)    (0.0948)      (0.0713)    (0.0031)    (0.0031)      (0.0633)    (0.0004)    (0.0004)      (0.0344)    (0.0001)    (0.0001)      (0.0097)    (0.1176) 
 
      Innovations Covariance Matrix     
           |  INFL   DUNRATE  DFEDFUNDS 
----------------------------------------
 INFL      | 0.0001    0        0.0010  
           |  (0)      (0)       (0)    
 DUNRATE   |  0       0.1000   -0.2000  
           |  (0)      (0)       (0)    
 DFEDFUNDS | 0.0010  -0.2000    1.6000  
           |  (0)      (0)       (0)

Сравните результаты с апостериором, в котором вы не задаете предшествующую регуляризацию.

PriorMdlNoReg = bayesvarm(numseries,numlags,'Model','normal','SeriesNames',seriesnames,...
    'Sigma',Sigma);
PosteriorMdlNoReg = estimate(PriorMdlNoReg,rmDataTable{:,seriesnames},'Display','equation');

Bayesian VAR under normal priors and fixed Sigma
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
                                                                                 VAR Equations                                                                                
           | INFL(-1)  DUNRATE(-1)  DFEDFUNDS(-1)  INFL(-2)  DUNRATE(-2)  DFEDFUNDS(-2)  INFL(-3)  DUNRATE(-3)  DFEDFUNDS(-3)  INFL(-4)  DUNRATE(-4)  DFEDFUNDS(-4)  Constant 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 INFL      |  0.1242     -0.4794        0.1007      0.3233     -0.0502        0.0450      0.4270      0.2734        0.0523      0.0168     -0.1823        0.0068      0.1010  
           | (0.0014)    (0.0028)      (0.0007)    (0.0016)    (0.0030)      (0.0007)    (0.0016)    (0.0029)      (0.0008)    (0.0016)    (0.0027)      (0.0007)    (0.0015) 
 DUNRATE   | -0.0264      0.3428        0.0089      0.0969      0.1578        0.0292      0.0042     -0.0309       -0.0114      0.0221     -0.1071        0.0072     -0.0873  
           | (0.0347)    (0.0714)      (0.0203)    (0.0356)    (0.0714)      (0.0203)    (0.0337)    (0.0670)      (0.0200)    (0.0326)    (0.0615)      (0.0186)    (0.0422) 
 DFEDFUNDS | -0.0351     -0.1248       -0.0411      0.0416     -0.0224       -0.1358      0.0014     -0.0302        0.1557     -0.0074     -0.0010       -0.0785     -0.0205  
           | (0.0787)    (0.0949)      (0.0696)    (0.0631)    (0.0689)      (0.0663)    (0.0533)    (0.0567)      (0.0630)    (0.0470)    (0.0493)      (0.0608)    (0.1347) 
 
      Innovations Covariance Matrix     
           |  INFL   DUNRATE  DFEDFUNDS 
----------------------------------------
 INFL      | 0.0001    0        0.0010  
           |  (0)      (0)       (0)    
 DUNRATE   |  0       0.1000   -0.2000  
           |  (0)      (0)       (0)    
 DFEDFUNDS | 0.0010  -0.2000    1.6000  
           |  (0)      (0)       (0)

Апостериорные оценки предшествующего Миннесоты имеют более низкую величину, в целом, по сравнению с оценками стандартной нормальной сопряженной предшествующей модели.

Настройте апостериорные Опции дискретизации

Открыть Live Script

Рассмотрим 3-D модель VAR (4) оценки апостериорного распределения В этом случае примите, что коэффициенты и ковариации матрицы являются независимыми (полусредняя предшествующая модель ).

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте полуконъюгатную предшествующую модель Bayesian VAR (4) для трех рядов откликов. Задайте имена переменных отклика.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'Model','semiconjugate',...
    'SeriesNames',seriesnames);

Потому что апостериор соединения полуконъюгатной предшествующей модели аналитически неразрешим, estimate использует семплер Гиббса, чтобы сформировать апостериор соединения путем выборки из отслеживаемых полных обусловленности.

Оцените апостериорное распределение. Для пробоотборника Гиббса укажите эффективное количество розыгрышей 20 000, период горения 5000 и коэффициент утончения 10.

rng(1) % For reproducibility
PosteriorMdl = estimate(PriorMdl,rmDataTable{:,seriesnames},...
    'Display','equation','NumDraws',20000,'Burnin',5000,'Thin',10);

Bayesian VAR under semiconjugate priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
                                                                                 VAR Equations                                                                                
           | INFL(-1)  DUNRATE(-1)  DFEDFUNDS(-1)  INFL(-2)  DUNRATE(-2)  DFEDFUNDS(-2)  INFL(-3)  DUNRATE(-3)  DFEDFUNDS(-3)  INFL(-4)  DUNRATE(-4)  DFEDFUNDS(-4)  Constant 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 INFL      |  0.2243     -0.0824        0.1365      0.2515     -0.0098        0.0329      0.2888      0.0311        0.0368      0.0458     -0.0206        0.0176      0.1836  
           | (0.0662)    (0.0821)      (0.0319)    (0.0701)    (0.0636)      (0.0309)    (0.0662)    (0.0534)      (0.0297)    (0.0649)    (0.0470)      (0.0274)    (0.0720) 
 DUNRATE   | -0.0262      0.3666        0.0148      0.0929      0.1637        0.0336      0.0016     -0.0147       -0.0089      0.0222     -0.1133        0.0082     -0.0808  
           | (0.0342)    (0.0728)      (0.0197)    (0.0354)    (0.0713)      (0.0198)    (0.0334)    (0.0671)      (0.0194)    (0.0320)    (0.0606)      (0.0179)    (0.0407) 
 DFEDFUNDS | -0.0251     -0.1285       -0.0527      0.0379     -0.0256       -0.1452     -0.0040     -0.0360        0.1516     -0.0090      0.0008       -0.0823     -0.0193  
           | (0.0785)    (0.0962)      (0.0673)    (0.0630)    (0.0688)      (0.0643)    (0.0531)    (0.0567)      (0.0610)    (0.0467)    (0.0492)      (0.0586)    (0.1302) 
 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.2984   -0.0219     0.1754  
           | (0.0305)  (0.0121)   (0.0499) 
 DUNRATE   | -0.0219    0.0890    -0.1496  
           | (0.0121)  (0.0092)   (0.0292) 
 DFEDFUNDS |  0.1754   -0.1496     1.4754  
           | (0.0499)  (0.0292)   (0.1506)

PosteriorMdl является empiricalbvarm модель, представленная рисунками из полных обусловленности. После удаления первого периода ожога рисует и утончает оставшиеся ничьи, сохраняя каждый 10-й розыгрыш, estimate сохраняет рисунки в CoeffDraws и SigmaDraws свойства.

Оценка модели VARX

Открыть Live Script

Рассмотрим 2-D модель VARX (1) для реального ВВП США (RGDP) и инвестиции (GCE) тарифы, которые лечат личное потребление (PCEC) скорость как экзогенная:

$[\begin{array}{llllllllllllllllllll} {RGDP}_{t} \\ {GCE}_{t} \end{array}] = c + Φ [\begin{array}{llllllllllllllllllll} {RGDP}_{t - 1} \\ {GCE}_{t - 1} \end{array}] + {PCEC}_{t} β + ε_{t} .$

Для всех $t$ , $ε_{t}$ - серия независимых 2-D нормальных инноваций со средним значением 0 и ковариацией $Σ$ . Примите следующие предыдущие распределения:

${[\begin{array}{c} Φ & c & β \end{array}]}^{'} | Σ \sim Ν_{4 \times 2} (Μ, V, Σ)$ , где M является матрицей средств 4 на 2 и $V$ - матрица шкалы между коэффициентами 4 на 4. Эквивалентно, $vec ({[\begin{array}{c} Φ & c & β \end{array}]}^{'}) | Σ \sim Ν_{8} (vec (Μ), Σ \otimes V)$ .
$Σ \sim Inverse Wishart (Ω, ν)$ , где И является матрицей шкалы 2 на 2 и $ν$ - степени свободы.

Загрузите набор макроэкономических данных США. Вычислите реальный показатель ВВП, инвестиций и личного потребления. Удалите все отсутствующие значения из получившейся серии.

load Data_USEconModel
DataTable.RGDP = DataTable.GDP./DataTable.GDPDEF;
seriesnames = ["PCEC"; "RGDP"; "GCE"];
rates = varfun(@price2ret,DataTable,'InputVariables',seriesnames);
rates = rmmissing(rates);
rates.Properties.VariableNames = seriesnames;

Создайте сопряженную предшествующую модель для параметров модели 2-D VARX (1).

numseries = 2;
numlags = 1;
numpredictors = 1;
PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,...
    'SeriesNames',seriesnames(2:end));

Оцените апостериорное распределение. Задайте экзогенные данные предиктора.

PosteriorMdl = estimate(PriorMdl,rates{:,2:end},...
    'X',rates{:,1},'Display','equation');

Bayesian VAR under conjugate priors
Effective Sample Size:          247
Number of equations:            2
Number of estimated Parameters: 8
                 VAR Equations                 
      | RGDP(-1)   GCE(-1)  Constant     X1    
-----------------------------------------------
 RGDP |  0.0083   -0.0027    0.0078    0.0105  
      | (0.0625)  (0.0606)  (0.0043)  (0.0625) 
 GCE  |  0.0059    0.0477    0.0166    0.0058  
      | (0.0644)  (0.0624)  (0.0044)  (0.0645) 
 
Innovations Covariance Matrix
      |   RGDP       GCE   
---------------------------
 RGDP |  0.0040    0.0000  
      | (0.0004)  (0.0003) 
 GCE  |  0.0000    0.0043  
      | (0.0003)  (0.0004)

По умолчанию estimate использует первые наблюдения p = 1 в заданных данных отклика в качестве предварительной выборки, и он удаляет соответствующие наблюдения в данных предиктора из выборки.

Апостериорные средства (и стандартные отклонения) коэффициентов регрессии появляются ниже X1 столбец сводной таблицы оценок.

Входные параметры

свернуть все

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

Предыдущая модель Bayesian VAR, заданная как объект модели в этой таблице.

Объект модели	Описание
`conjugatebvarm`	Зависимая, матричная-нормальная-обратная-Wishart сопряженная модель, возвращенная `bayesvarm`, `conjugatebvarm`, или `estimate`
`semiconjugatebvarm`	Независимая, нормальная-обратная-Wishart полусредняя предыдущая модель, возвращенная `bayesvarm` или `semiconjugatebvarm`
`diffusebvarm`	Диффузная предыдущая модель, возвращенная `bayesvarm` или `diffusebvarm`
`normalbvarm`	Нормальная сопряженная модель с фиксированной инновационной ковариационной матрицей, возвращенной `bayesvarm`, `normalbvarm`, или `estimate`

PriorMdl может также представлять апостериорную модель соединения, возвращенную estimate, либо a conjugatebvarm или normalbvarm объект модели. В этом случае, estimate обновляет апостериорное распределение соединений с помощью новых наблюдений.

Для semiconjugatebvarm модель, estimate использует семплер Гиббса, чтобы оценить апостериорное распределение. Для настройки семплера смотрите Опции для Semiconjugate Previous Distributions.

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

Наблюдался многомерный ряд отклика, на который estimate подходит для модели, заданной как numobs-by- numseries числовая матрица.

numobs - размер выборки. numseries - количество переменных отклика (PriorMdl.NumSeries).

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. Столбцы соответствуют отдельным переменным отклика.

Y представляет продолжение предварительной серии откликов в Y0.

Типы данных: double

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: 'Y0',Y0,'Display','off' задает предварительный образец данных Y0 и подавляет отображение оценки.

Опции для всех предыдущих распределений

свернуть все

`'Y0'` - Предварительный образец данных отклика
числовая матрица

Предварительный образец данных отклика для инициализации модели VAR для оценки, заданный как разделенная разделенными запятой парами, состоящая из 'Y0' и a numpreobs-by- numseries числовая матрица. numpreobs - количество предварительных наблюдений.

Строки соответствуют предварительным образцам наблюдений, а последняя строка содержит последнее наблюдение. Y0 должно иметь по крайней мере PriorMdl.P строки. Если вы поставляете больше строк, чем нужно, estimate использует последние PriorMdl.P только наблюдения.

Столбцы должны соответствовать ряду ответов в Y.

По умолчанию, estimate использует Y(1:PriorMdl.P,:) в качестве предварительного примера наблюдений, а затем оценивает апостериорное использование Y((PriorMdl.P + 1):end,:). Это действие уменьшает эффективный размер выборки.

Типы данных: double

`'X'` - Данные предиктора
числовая матрица

Данные предиктора для компонента экзогенной регрессии в модели, заданные как разделенная разделенными запятой парами, состоящая из 'X' и a numobs-by- PriorMdl.NumPredictors числовая матрица.

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. estimate не использует регрессионный компонент в предварительном образце периода. X должно иметь, по крайней мере, столько наблюдений, сколько наблюдений, используемых после периода предварительного образца.

Если вы задаете Y0, затем X должно иметь по крайней мере numobs строки (см. Y).
В противном случае X должно иметь по крайней мере numobs – PriorMdl.P наблюдения для расчета удаления предварительного образца.

В любом случае, если вы поставляете больше строк, чем необходимо, estimate использует только последние наблюдения.

Столбцы соответствуют отдельным переменным предиктора. Все переменные предиктора присутствуют в регрессионном компоненте каждого уравнения отклика.

Типы данных: double

`'Display'` - Стиль отображения оценки
`'table'` (по умолчанию) | `'off'` | `'equation'` | `'matrix'`

Стиль отображения оценки, напечатанный в командной строке, задается как разделенная разделенными запятой парами, состоящая из 'Display' и значение в этой таблице.

Значение	Описание
`'off'`	`estimate` не печатается в командной строке.
`'table'`	`estimate` печатает следующее: Информация об оценке Табличные сводные данные апостериорных средств коэффициентов и стандартных отклонений; каждая строка соответствует коэффициенту, и каждый столбец соответствует типу оценки Апостериорное среднее из инноваций ковариации матрице со стандартными отклонениями в круглых скобках
`'equation'`	`estimate` печатает следующее: Информация об оценке табличные сводные данные апостериорных средств и стандартных отклонений; каждая строка соответствует переменной отклика в системе, и каждый столбец соответствует коэффициенту в уравнении (для примера обозначенный столбец `Y1(-1)` содержит оценки коэффициента задержки 1 первой переменной отклика в каждом уравнении) Апостериорное среднее из инноваций ковариации матрицу со стандартными отклонениями в круглых скобках.
`'matrix'`	`estimate` печатает следующее: Информация об оценке Отделите табличные отображения следующих средств и стандартных отклонений (в круглых скобках) для каждого параметра в модели Φ1..., _{Φ <reservedrangesplaceholder2>}, c, δ, Β, и Σ

Информация об оценке включает в себя эффективный размер выборки, количество уравнений в системе и количество оцененных параметров.

Пример: 'Display','matrix'

Типы данных: char | string

Опции для Semiconjugate Previous Distributions

свернуть все

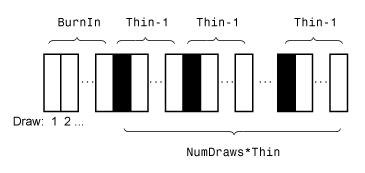
`'NumDraws'` - Моделирование Монте-Карло скорректированный размер выборки
`1e5` (по умолчанию) | положительное целое число

Симуляция Монте-Карло скорректированный размер выборки, заданный как разделенная разделенными запятой парами, состоящая из 'NumDraws' и положительное целое число. estimate фактически рисует BurnIn + NumDraws*Thin выборки, но основывает оценки на NumDraws выборки. Для получения дополнительной информации о том, как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.

Пример: 'NumDraws',1e7

Типы данных: double

`'BurnIn'` - Количество ничьих для удаления из начала выборки Монте-Карло
`5000` (по умолчанию) | неотрицательной скаляром

Количество розыгрышей для удаления из начала выборки Монте-Карло для уменьшения переходных эффектов, заданное как разделенная разделенными запятой парами, состоящая из 'BurnIn' и неотрицательный скаляр. Для получения дополнительной информации о том, как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.

Совет

Чтобы помочь вам указать соответствующий размер периода горения:

Определите степень переходного поведения в выборке путем определения 'BurnIn',0.
Симулируйте несколько тысяч наблюдений при помощи simulate.
Нарисуйте графики трассировки.

Пример: 'BurnIn',0

Типы данных: double

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

Скорректированный множитель размера выборки, заданный как разделенная разделенными запятой парами, состоящая из 'Thin' и положительное целое число.

Фактический размер выборки Монте-Карло BurnIn + NumDraws*Thin. После отбрасывания горения, estimate отбрасывает каждый Thin – 1 рисует, а затем сохраняет следующий. Для получения дополнительной информации о том, как estimate уменьшает полную выборку Монте-Карло, см. Алгоритмы.

Совет

Чтобы уменьшить потенциальную большую последовательную корреляцию в выборке Монте-Карло или уменьшить потребление памяти рисунков, сохраненных в PosteriorMdl, задайте большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

`'Coeff0'` - Стартовые значения коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

Начальные значения коэффициентов модели VAR для семплера Гиббса, заданные как разделенная разделенными запятой парами, состоящая из 'Coeff0' и a numel(PriorMdl.Mu)-by-1 числовой вектор-столбец.

Элементы соответствуют элементам PriorMdl.Mu (см. Mu).

По умолчанию Coeff0 - обычная оценка методом наименьших квадратов (OLS).

Совет

Создание Coeff0 путем вертикального сложения транспонирования всех начальных коэффициентов в следующем порядке (коэффициенты пропуска не в модели):
1. Все матрицы коэффициентов, упорядоченные по задержке
2. Вектор константы
3. Вектор линейного временного тренда
4. Матрица экзогенного коэффициента регрессии
Задайте векторизованный результат Coeff0(:).
Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметра. Проверьте, что решения из каждого запуска сходятся к аналогичным значениям.

Типы данных: double

`'Sigma0'` - Стартовые значения ковариационной матрицы инноваций для семплера Гиббса
числовая положительная определенная матрица

Начальные значения ковариационной матрицы инноваций для семплера Гиббса, заданные как разделенная разделенными запятой парами, состоящая из 'Sigma0' и числовую положительно определенную матрицу. Строки и столбцы соответствуют уравнениям отклика.

По умолчанию Sigma0 - остаточная средняя квадратичная невязка OLS.

Совет

Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметра. Проверьте, что решения из каждого запуска сходятся к аналогичным значениям.

Типы данных: double

Выходные аргументы

свернуть все

`PosteriorMdl` - Апостериорная байесовская модель VAR
`conjugatebvarm` объект модели | `normalbvarm` объект модели | `empiricalbvarm` объект модели

Апостериорная байесовская модель VAR, возвращенная как объект модели в таблице.

Объект модели	`PriorMdl`	Апостериорная форма
`conjugatebvarm`	`conjugatebvarm` или `diffusebvarm`	Аналитически отслеживаемый
`normalbvarm`	`normalbvarm`	Аналитически отслеживаемый
`empiricalbvarm`	`semiconjugatebvarm`	Аналитически неразрешимый

`Summary` - Сводные данные байесовских оценок
массив структур

Сводные данные байесовских оценок, возвращенная как массив структур, содержащий поля в этой таблице.

Область	Описание	Тип данных
`Description`	Описание модели	Строковый скаляр
`NumEstimatedParameters`	Количество предполагаемых коэффициентов	Числовой скаляр
`Table`	Таблица апостериорных средств коэффициентов и стандартных отклонений; каждая строка соответствует коэффициенту, и каждый столбец соответствует типу оценки	Таблица
`CoeffMap`	Имена коэффициентов	Строковый вектор
`CoeffMean`	Апостериорное средство коэффициента	Числовой вектор; строки соответствуют `CoeffMap`
`CoeffStd`	Апостериорные стандартные отклонения коэффициента	Числовой вектор; строки соответствуют `CoeffMap`
`SigmaMean`	Инновации ковариационная апостериорная матрица	Числовая матрица; строки и столбцы соответствуют ответным уравнениям
`SigmaStd`	Инновации ковариационная апостериорная матрица стандартного отклонения	Числовая матрица; строки и столбцы соответствуют ответным уравнениям

В качестве альтернативы передайте PosteriorMdl кому summarize для получения сводных данных байесовских оценок.

Подробнее о

свернуть все

Байесовский вектор векторной авторегрессии (VAR)

A Bayesian VAR model обрабатывает все коэффициенты и ковариационную матрицу инноваций как случайные переменные в m -мерной, стационарной модели VARX (p). Модель имеет одну из трех форм, описанных в этой таблице.

Модель	Уравнение
VAR (p) редуцированной формы в обозначении разностного уравнения	$y_{t} = Φ_{1} y_{t - 1} + ... + Φ_{p} y_{t - p} + c + δ t + Β x_{t} + ε_{t} .$
Многомерная регрессия	$y_{t} = Z_{t} λ + ε_{t} .$
Матричная регрессия	$y_{t} = Λ^{'} z_{t}^{'} + ε_{t} .$

Для каждого временного t = 1,..., T:

_yt - m -мерный вектор наблюдаемой отклика, где m = numseries.
_Φ1,..._, - p являются m -by m матрицами коэффициентов AR лагов с 1 по p, где p = numlags.
c - вектор m -by-1 констант модели, если IncludeConstant является true.
δ - вектор m -by-1 коэффициентов линейного временного тренда, если IncludeTrend является true.
Β - m -by - r матрица коэффициентов регрессии вектора r -by - 1 наблюдаемых экзогенных предикторов x t, где r = NumPredictors. Все переменные предиктора появляются в каждом уравнении.
$z_{t} = [\begin{matrix} y_{t - 1}^{'} & y_{t - 2}^{'} & \dots & y_{t - p}^{'} & 1 & t & x_{t}^{'} \end{matrix}],$ который является вектором 1-by- (mp + r + 2), и _Z t является m -by- m (mp + r + 2) блочной диагональной матрицей

$[\begin{matrix} z_{t} & 0_{z} & \dots & 0_{z} \\ 0_{z} & z_{t} & \dots & 0_{z} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0_{z} & 0_{z} & 0_{z} & z_{t} \end{matrix}],$
где 0 z является 1-бай- (mp + r + 2) вектором нулей.
$Λ = {[\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}]}^{'}$ , которая является (mp + r + 2) -by m случайной матрицей коэффициентов, и m (mp + r + 2) -by-1 вектор λ = vec (
_εt является m-на-1 вектором случайных, последовательно некоррелированных, многомерных нормальных инноваций с нулевым вектором для среднего и m -by- m матрицы Это предположение подразумевает, что вероятность данных является

$ℓ (Λ, Σ | y, x) = \prod_{t = 1}^{T} f (y_{t}; Λ, Σ, z_{t}),$
где f m - размерная многомерная нормальная плотность со средним <reservedrangesplaceholder3> <reservedrangesplaceholder2> Λ и ковариацией Σ, оценен в <reservedrangesplaceholder1> <reservedrangesplaceholder0>.

Прежде, чем рассмотреть данные, Вы налагаете joint prior distribution предположение на (Λ,Σ), которым управляет распределение π (Λ,Σ). В байесовском анализе распределение параметров обновляется информацией о параметрах, полученных из вероятности данных. Результатом является joint posterior distribution π (Λ,Σ|<reservedrangesplaceholder2>,<reservedrangesplaceholder1>,<reservedrangesplaceholder0>0), где:

Y - T матрица m, содержащая весь ряд ответов _{y t}, t = 1,..., T.
X - T матрица m, содержащая весь экзогенный ряд _{x t}, t = 1,..., T.
Y 0 является p -by - m матрицей предварительных образцов данных, используемых для инициализации модели VAR для оценки.

Совет

Симуляция Монте-Карло подвержена изменениям. Если estimate использует симуляцию Монте-Карло, тогда оценки и выводы могут варьироваться при вызове estimate несколько раз при, казалось бы, эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите начальное число случайных чисел при помощи rng перед вызовом estimate.

Алгоритмы

Всякий раз, когда предшествующее распределение PriorMdl и вероятность данных дает аналитически отслеживаемое апостериорное распределение, estimate оценивает решения закрытой формы для оценок Байеса. В противном случае, estimate использует семплер Гиббса, чтобы оценить апостериор.
Этот рисунок иллюстрирует, как estimate уменьшает выборку Монте-Карло, используя значения NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные вытяжки из распределения. estimate удаляет белые прямоугольники из выборки Монте-Карло. Оставшиеся NumDraws чёрные прямоугольники составляют выборку Монте-Карло.

См. также

Объекты

conjugatebvarm | diffusebvarm | empiricalbvarm | normalbvarm | semiconjugatebvarm

Документация

estimate

Синтаксис

Описание

Примеры

Оценка апостериорного распределения

Задайте данные предварительного образца

Просмотр и возврат сводных данных оценок

Оценка апостериорной функции с разреженными коэффициентами

Настройте апостериорные Опции дискретизации

Оценка модели VARX

Входные параметры

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

Аргументы в виде пар имя-значение

`'Y0'` - Предварительный образец данных отклика
числовая матрица

`'X'` - Данные предиктора
числовая матрица

`'Display'` - Стиль отображения оценки
`'table'` (по умолчанию) | `'off'` | `'equation'` | `'matrix'`

`'NumDraws'` - Моделирование Монте-Карло скорректированный размер выборки
`1e5` (по умолчанию) | положительное целое число

`'BurnIn'` - Количество ничьих для удаления из начала выборки Монте-Карло
`5000` (по умолчанию) | неотрицательной скаляром

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

`'Coeff0'` - Стартовые значения коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

`'Sigma0'` - Стартовые значения ковариационной матрицы инноваций для семплера Гиббса
числовая положительная определенная матрица

Выходные аргументы

`PosteriorMdl` - Апостериорная байесовская модель VAR
`conjugatebvarm` объект модели | `normalbvarm` объект модели | `empiricalbvarm` объект модели

`Summary` - Сводные данные байесовских оценок
массив структур

Подробнее о

Байесовский вектор векторной авторегрессии (VAR)

Совет

Алгоритмы

См. также

Объекты

Функции

Документация по Econometrics Toolbox

Поддержка

Документация

estimate

Синтаксис

Описание

Примеры

Оценка апостериорного распределения

Задайте данные предварительного образца

Просмотр и возврат сводных данных оценок

Оценка апостериорной функции с разреженными коэффициентами

Настройте апостериорные Опции дискретизации

Оценка модели VARX

Входные параметры

PriorMdl - Предыдущая байесовская модель VAR conjugatebvarm объект модели | semiconjugatebvarm объект модели | diffusebvarm объект модели | normalbvarm объект модели

Y - Наблюдаемый многомерный ряд отклика числовая матрица

Аргументы в виде пар имя-значение

'Y0' - Предварительный образец данных отклика числовая матрица

'X' - Данные предиктора числовая матрица

'Display' - Стиль отображения оценки 'table' (по умолчанию) | 'off' | 'equation' | 'matrix'

'NumDraws' - Моделирование Монте-Карло скорректированный размер выборки 1e5 (по умолчанию) | положительное целое число

'BurnIn' - Количество ничьих для удаления из начала выборки Монте-Карло 5000 (по умолчанию) | неотрицательной скаляром

'Thin' - Скорректированный множитель размера выборки 1 (по умолчанию) | положительное целое число

'Coeff0' - Стартовые значения коэффициентов модели VAR для дискретизатора Гиббса числовые векторы-столбцы

'Sigma0' - Стартовые значения ковариационной матрицы инноваций для семплера Гиббса числовая положительная определенная матрица

Выходные аргументы

PosteriorMdl - Апостериорная байесовская модель VAR conjugatebvarm объект модели | normalbvarm объект модели | empiricalbvarm объект модели

Summary - Сводные данные байесовских оценок массив структур

Подробнее о

Байесовский вектор векторной авторегрессии (VAR)

Совет

Алгоритмы

См. также

Объекты

Функции

Документация по Econometrics Toolbox

Поддержка

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

`'Y0'` - Предварительный образец данных отклика
числовая матрица

`'X'` - Данные предиктора
числовая матрица

`'Display'` - Стиль отображения оценки
`'table'` (по умолчанию) | `'off'` | `'equation'` | `'matrix'`

`'NumDraws'` - Моделирование Монте-Карло скорректированный размер выборки
`1e5` (по умолчанию) | положительное целое число

`'BurnIn'` - Количество ничьих для удаления из начала выборки Монте-Карло
`5000` (по умолчанию) | неотрицательной скаляром

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

`'Coeff0'` - Стартовые значения коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

`'Sigma0'` - Стартовые значения ковариационной матрицы инноваций для семплера Гиббса
числовая положительная определенная матрица

`PosteriorMdl` - Апостериорная байесовская модель VAR
`conjugatebvarm` объект модели | `normalbvarm` объект модели | `empiricalbvarm` объект модели

`Summary` - Сводные данные байесовских оценок
массив структур