simulate

Симулируйте коэффициенты и инновации ковариационной матрицы модели Байесовской векторной авторегрессии (VAR)

Синтаксис

[Coeff,Sigma]
= simulate(PriorMdl)

[Coeff,Sigma]
= simulate(PriorMdl,Y)

[Coeff,Sigma]
= simulate(___,Name,Value)

Описание

пример

[Coeff,Sigma] = simulate(PriorMdl) возвращает случайный вектор коэффициентов Coeff и случайные инновации ковариации матричных Sigma получен из предыдущей байесовской модели VAR (p) PriorMdl.

пример

[Coeff,Sigma] = simulate(PriorMdl,Y) черпает из апостериорных распределений, произведенных или обновленных путем включения данных отклика Y.

NaNs в данных указывают отсутствующие значения, которые simulate удаляет при помощи спискового удаления.

пример

[Coeff,Sigma] = simulate(___,Name,Value) задает опции, использующие один или несколько аргументы пары "имя-значение" в дополнение к любой комбинации входных аргументов в предыдущих синтаксисах. Для примера можно задать количество случайных рисований из распределения или указать данные отклика предварительного образца.

Примеры

свернуть все

Нарисуйте коэффициенты и инновации Ковариации матрице из предыдущего распределения

Открыть Live Script

Рассмотрим 3-D модель VAR (4) для инфляции в США (INFL), безработица (UNRATE), и федеральные фонды (FEDFUNDS) ставки.

$[\begin{array}{llllllllllllllllllll} {INFL}_{t} \\ {UNRATE}_{t} \\ {FEDFUNDS}_{t} \end{array}] = c + \sum_{j = 1}^{4} Φ_{j} [\begin{array}{llllllllllllllllllll} {INFL}_{t - j} \\ {UNRATE}_{t - j} \\ {FEDFUNDS}_{t - j} \end{array}] + [\begin{array}{cccccccccccccccccccc} ε_{1, t} \\ ε_{2, t} \\ ε_{3, t} \end{array}] .$

Для всех $t$ , $ε_{t}$ - серия независимых 3-D нормальных инноваций со средним значением 0 и ковариацией $Σ$ . Предположим, что сопряженное предшествующее распределение $π ({[Φ_{1}, . . ., Φ_{4}, c]}^{'}, Σ)$ управляет поведением параметров.

Создайте сопряженную предшествующую модель. Задайте имена рядов ответов. Получите сводные данные предыдущего распределения.

seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'ModelType','conjugate',...
    'SeriesNames',seriesnames);
Summary = summarize(PriorMdl,'off');

Нарисуйте набор коэффициентов и ковариационную матрицу инноваций из предыдущего распределения.

rng(1) % For reproducibility
[Coeff,Sigma] = simulate(PriorMdl);

Отобразите выбранные коэффициенты с соответствующими именами и ковариационной матрицей инноваций.

table(Coeff,'RowNames',Summary.CoeffMap)

ans=39×1 table
                     Coeff   
                   __________

    AR{1}(1,1)        0.44999
    AR{1}(1,2)       0.047463
    AR{1}(1,3)      -0.042106
    AR{2}(1,1)     -0.0086264
    AR{2}(1,2)       0.034049
    AR{2}(1,3)      -0.058092
    AR{3}(1,1)      -0.015698
    AR{3}(1,2)      -0.053203
    AR{3}(1,3)      -0.031138
    AR{4}(1,1)       0.036431
    AR{4}(1,2)      -0.058279
    AR{4}(1,3)       -0.02195
    Constant(1)        -1.001
    AR{1}(2,1)      -0.068182
    AR{1}(2,2)        0.51029
    AR{1}(2,3)      -0.094367
      ⋮

AR {r} (j, k) является коэффициентом AR переменной отклика k (отстающие r модулей) в ответном уравнении j.

Sigma

Sigma = 3×3

    0.1238   -0.0053   -0.0369
   -0.0053    0.0456    0.0160
   -0.0369    0.0160    0.1039

Строки и столбцы Sigma соответствуют нововведениям в уравнениях отклика, упорядоченных PriorMdl.SeriesNames.

Симулируйте параметры из аналитически отслеживаемого апостериорного распределения

Открыть Live Script

Рассмотрим 3-D модель VAR (4) коэффициентов рисования и инноваций Ковариации матрицы из предыдущего распределения. В этом случае примите, что предшествующее распределение является диффузным.

Загрузка и предварительная обработка данных

Загрузите набор макроэкономических данных США. Рассчитать уровень инфляции, стабилизировать ставки по безработице и федеральным фондам и удалить отсутствующие значения.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте предыдущую модель

Создайте диффузную модель Bayesian VAR (4) для трех рядов откликов. Задайте имена рядов ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'SeriesNames',seriesnames);

Оценка апостериорного распределения

Оцените апостериорное распределение. Верните сводные данные оценок.

[PosteriorMdl,Summary] = estimate(PriorMdl,rmDataTable{:,seriesnames});

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
             |   Mean     Std  
-------------------------------
 Constant(1) |  0.1007  0.0832 
 Constant(2) | -0.0499  0.0450 
 Constant(3) | -0.4221  0.1781 
 AR{1}(1,1)  |  0.1241  0.0762 
 AR{1}(2,1)  | -0.0219  0.0413 
 AR{1}(3,1)  | -0.1586  0.1632 
 AR{1}(1,2)  | -0.4809  0.1536 
 AR{1}(2,2)  |  0.4716  0.0831 
 AR{1}(3,2)  | -1.4368  0.3287 
 AR{1}(1,3)  |  0.1005  0.0390 
 AR{1}(2,3)  |  0.0391  0.0211 
 AR{1}(3,3)  | -0.2905  0.0835 
 AR{2}(1,1)  |  0.3236  0.0868 
 AR{2}(2,1)  |  0.0913  0.0469 
 AR{2}(3,1)  |  0.3403  0.1857 
 AR{2}(1,2)  | -0.0503  0.1647 
 AR{2}(2,2)  |  0.2414  0.0891 
 AR{2}(3,2)  | -0.2968  0.3526 
 AR{2}(1,3)  |  0.0450  0.0413 
 AR{2}(2,3)  |  0.0536  0.0223 
 AR{2}(3,3)  | -0.3117  0.0883 
 AR{3}(1,1)  |  0.4272  0.0860 
 AR{3}(2,1)  | -0.0389  0.0465 
 AR{3}(3,1)  |  0.2848  0.1841 
 AR{3}(1,2)  |  0.2738  0.1620 
 AR{3}(2,2)  |  0.0552  0.0876 
 AR{3}(3,2)  | -0.7401  0.3466 
 AR{3}(1,3)  |  0.0523  0.0428 
 AR{3}(2,3)  |  0.0008  0.0232 
 AR{3}(3,3)  |  0.0028  0.0917 
 AR{4}(1,1)  |  0.0167  0.0901 
 AR{4}(2,1)  |  0.0285  0.0488 
 AR{4}(3,1)  | -0.0690  0.1928 
 AR{4}(1,2)  | -0.1830  0.1520 
 AR{4}(2,2)  | -0.1795  0.0822 
 AR{4}(3,2)  |  0.1494  0.3253 
 AR{4}(1,3)  |  0.0067  0.0395 
 AR{4}(2,3)  |  0.0088  0.0214 
 AR{4}(3,3)  | -0.1372  0.0845 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

PosteriorMdl является conjugatebvarm модель, которая аналитически отслеживается.

Симулируйте параметры из апостериорной функции

Нарисуйте 1000 выборки из апостериорного распределения.

rng(1)
[Coeff,Sigma] = simulate(PosteriorMdl,'NumDraws',1000);

Coeff - матрица 39 на 1000 случайным образом нарисованных коэффициентов. Каждый столбец является индивидуальным рисунком, и каждая строка является индивидуальным коэффициентом. Sigma является массивом 3х3-х1000 случайным образом нарисованных инноваций ковариации матрицах. Каждая страница является индивидуальным розыгрышем.

Отобразите первый коэффициент, полученный из распределения с соответствующими именами параметров, и отобразите первую нарисованную ковариационную матрицу инноваций.

Coeffs = table(Coeff(:,1),'RowNames',Summary.CoeffMap)

Coeffs=39×1 table
                     Var1   
                   _________

    AR{1}(1,1)       0.14994
    AR{1}(1,2)      -0.46927
    AR{1}(1,3)      0.088388
    AR{2}(1,1)       0.28139
    AR{2}(1,2)      -0.19597
    AR{2}(1,3)      0.049222
    AR{3}(1,1)        0.3946
    AR{3}(1,2)      0.081871
    AR{3}(1,3)      0.002117
    AR{4}(1,1)       0.13514
    AR{4}(1,2)      -0.23661
    AR{4}(1,3)      -0.01869
    Constant(1)     0.035787
    AR{1}(2,1)     0.0027895
    AR{1}(2,2)       0.62382
    AR{1}(2,3)      0.053232
      ⋮

Sigma(:,:,1)

ans = 3×3

    0.2653   -0.0075    0.1483
   -0.0075    0.1015   -0.1435
    0.1483   -0.1435    1.5042

Симулируйте параметры из аналитически неразрешимого апостериорного распределения

Открыть Live Script

Загрузка и предварительная обработка данных

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте предыдущую модель

Создайте полуконъюгатную предшествующую модель Bayesian VAR (4) для трех рядов откликов. Задайте имена переменных отклика.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'Model','semiconjugate',...
    'SeriesNames',seriesnames);

Симулируйте параметры из апостериорной функции

Поскольку апостериорное распределение соединений полуконъюгатной предшествующей модели аналитически неразрешимо, simulate последовательно черпает из полных условных распределений.

Нарисуйте 1000 выборки из апостериорного распределения. Задайте период горения 10 000 и коэффициент утончения 5. Запустите семплер Гиббса, приняв апостериорное среднее $Σ$ - матрица 3-D тождеств.

rng(1)
[Coeff,Sigma] = simulate(PriorMdl,rmDataTable{:,seriesnames},...
    'NumDraws',1000,'BurnIn',1e4,'Thin',5,'Sigma0',eye(3));

Симулируйте коэффициенты из модели VARX

Открыть Live Script

Рассмотрим 2-D модель VARX (1) для реального ВВП США (RGDP) и инвестиции (GCE) тарифы, которые лечат личное потребление (PCEC) скорость как экзогенная:

$[\begin{array}{llllllllllllllllllll} {RGDP}_{t} \\ {GCE}_{t} \end{array}] = c + Φ [\begin{array}{llllllllllllllllllll} {RGDP}_{t - 1} \\ {GCE}_{t - 1} \end{array}] + {PCEC}_{t} β + ε_{t} .$

Для всех $t$ , $ε_{t}$ - серия независимых 2-D нормальных инноваций со средним значением 0 и ковариацией $Σ$ . Примите следующие предыдущие распределения:

${[\begin{array}{c} Φ & c & β \end{array}]}^{'} | Σ \sim Ν_{4 \times 2} (Μ, V, Σ)$ , где M является матрицей средств 4 на 2 и $V$ - матрица шкалы между коэффициентами 4 на 4. Эквивалентно, $vec ({[\begin{array}{c} Φ & c & β \end{array}]}^{'}) | Σ \sim Ν_{8} (vec (Μ), Σ \otimes V)$ .
$Σ \sim I n v e r s e W i s h a r t (Ω, ν),$ где И - матрица шкалы 2 на 2, $ν$ - степени свободы.

Загрузите набор макроэкономических данных США. Вычислите реальный показатель ВВП, инвестиций и личного потребления. Удалите все отсутствующие значения из получившейся серии.

load Data_USEconModel
DataTable.RGDP = DataTable.GDP./DataTable.GDPDEF;
seriesnames = ["PCEC"; "RGDP"; "GCE"];
rates = varfun(@price2ret,DataTable,'InputVariables',seriesnames);
rates = rmmissing(rates);
rates.Properties.VariableNames = seriesnames;

Создайте сопряженную предшествующую модель для параметров модели 2-D VARX (1).

numseries = 2;
numlags = 1;
numpredictors = 1;
PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,...
    'SeriesNames',seriesnames(2:end));

Симулируйте непосредственно из апостериорного распределения. Задайте экзогенные данные предиктора.

[Coeff,Sigma] = simulate(PriorMdl,rates{:,PriorMdl.SeriesNames},...
    'X',rates{:,seriesnames(1)});

По умолчанию simulate использует первые наблюдения p = 1 данных отклика, чтобы инициализировать динамический компонент модели, и удаляет соответствующие наблюдения из данных предиктора.

Входные параметры

свернуть все

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

Предыдущая модель Bayesian VAR, заданная как объект модели в этой таблице.

Объект модели	Описание
`conjugatebvarm`	Зависимая, матричная-нормальная-обратная-Wishart сопряженная модель, возвращенная `bayesvarm` или `conjugatebvarm`
`semiconjugatebvarm`	Независимая, нормальная-обратная-Wishart полусредняя предыдущая модель, возвращенная `bayesvarm` или `semiconjugatebvarm`
`diffusebvarm`	Диффузная предыдущая модель, возвращенная `bayesvarm` или `diffusebvarm`
`normalbvarm`	Нормальная сопряженная модель с фиксированной инновационной ковариационной матрицей, возвращенной `bayesvarm` или `normalbvarm`

Примечание

Если PriorMdl является diffusebvarm модель, тогда вы также должны поставить Y потому что simulate невозможно получить из неподходящего предыдущего распределения. Следовательно, Coeff и Sigma represent черпает из апостериорного распределения.

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

Наблюдался многомерный ряд отклика, на который simulate подходит для модели, заданной как numobs-by- numseries числовая матрица.

numobs - размер выборки. numseries - количество переменных отклика (PriorMdl.NumSeries).

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. Столбцы соответствуют отдельным переменным отклика.

Y представляет продолжение предварительной серии откликов в Y0.

Типы данных: double

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: 'Y0',Y0,'X',X задает предварительные данные отклика Y0 для инициализации модели VAR для апостериорной оценки и данных предиктора X для компонента экзогенной регрессии.

Опции для всех предыдущих распределений

свернуть все

`'NumDraws'` - Количество случайных рисок
`1` (по умолчанию) | положительное целое число

Количество случайных рисований из распределений, заданное как разделенная разделенными запятой парами, состоящая из 'NumDraws' и положительное целое число.

Пример: 'NumDraws',1e7

Типы данных: double

`'Y0'` - Предварительный образец данных отклика
числовая матрица

Предварительный образец данных отклика для инициализации модели VAR для оценки, заданный как разделенная разделенными запятой парами, состоящая из 'Y0' и a numpreobs-by- numseries числовая матрица. numpreobs - количество предварительных наблюдений.

Строки соответствуют предварительным образцам наблюдений, а последняя строка содержит последнее наблюдение. Y0 должно иметь по крайней мере PriorMdl.P строки. Если вы поставляете больше строк, чем нужно, simulate использует последние PriorMdl.P только наблюдения.

Столбцы должны соответствовать ряду ответов в Y.

По умолчанию, simulate использует Y(1:PriorMdl.P,:) в качестве предварительного примера наблюдений, а затем оценивает апостериорное использование Y((PriorMdl.P + 1):end,:). Это действие уменьшает эффективный размер выборки.

Типы данных: double

`'X'` - Данные предиктора
числовая матрица

Данные предиктора для компонента экзогенной регрессии в модели, заданные как разделенная разделенными запятой парами, состоящая из 'X' и a numobs-by- PriorMdl.NumPredictors числовая матрица.

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. simulate не использует регрессионный компонент в предварительном образце периода. X должно иметь, по крайней мере, столько наблюдений, сколько наблюдений, используемых после периода предварительного образца.

Если вы задаете Y0, затем X должно иметь по крайней мере numobs строки (см. Y).
В противном случае X должно иметь по крайней мере numobs – PriorMdl.P наблюдения для расчета удаления предварительного образца.

В любом случае, если вы поставляете больше строк, чем необходимо, simulate использует только последние наблюдения.

Столбцы соответствуют отдельным переменным предиктора. Все переменные предиктора присутствуют в регрессионном компоненте каждого уравнения отклика.

Типы данных: double

Опции для Semiconjugate Previous Distributions

свернуть все

`'BurnIn'` - Количество розыгрышей для удаления из начала выборки
`0` (по умолчанию) | неотрицательной скаляром

Количество розыгрышей для удаления из начала выборки для уменьшения переходных эффектов, заданное как разделенная разделенными запятой парами, состоящая из 'BurnIn' и неотрицательный скаляр. Для получения дополнительной информации о том, как simulate уменьшает полную выборку, см. Алгоритмы.

Совет

Чтобы помочь вам указать соответствующий размер периода горения:

Определите степень переходного поведения в выборке путем определения 'BurnIn',0.
Симулируйте несколько тысяч наблюдений при помощи simulate.
Нарисуйте графики трассировки.

Пример: 'BurnIn',0

Типы данных: double

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

Скорректированный множитель размера выборки, заданный как разделенная разделенными запятой парами, состоящая из 'Thin' и положительное целое число.

Фактический размер выборки BurnIn + NumDraws*Thin. После отбрасывания горения, simulate отбрасывает каждый Thin – 1 рисует, а затем сохраняет следующий розыгрыш. Для получения дополнительной информации о том, как simulate уменьшает полную выборку, см. Алгоритмы.

Совет

Чтобы уменьшить потенциальную большую последовательную корреляцию в выборке или уменьшить потребление памяти рисунков, сохраненных в Coeff и Sigma, задайте большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

`'Coeff0'` - Начальное значение коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

Начальное значение коэффициентов модели VAR для семплера Гиббса, заданное как разделенная разделенными запятой парами, состоящая из 'Coeff0' и числовой вектор-столбец с (PrivateMdl.NumSeries * k) -by- NumDraws элементы, где k = PriorMdl. NumSeries*PriorMdl. P + PriorMdl. IncludeIntercept + PriorMdl. IncludeTrend + PriorMdl. NumPredictors, которое является количеством коэффициентов в уравнении отклика. Для получения дополнительной информации о структуре Coeff0, см. выход Coeff.

По умолчанию Coeff0 - многомерная оценка методом наименьших квадратов.

Совет

Чтобы задать Coeff0:
1. Установите отдельные переменные для начальных значений каждой матрицы коэффициентов и вектора.
2. Горизонтально конкатенируйте все средства коэффициентов в этом порядке:
  
  $C o e f f = [\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}] .$
3. Векторизация транспонирования средней матрицы коэффициентов.
  Coeff0 = Coeff.'; Coeff0 = Coeff0(:);
Хорошей практикой является запуск simulate несколько раз с различными начальными значениями параметра. Проверьте, что оценки из каждого запуска сходятся к аналогичным значениям.

Типы данных: double

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

Начальное значение ковариационной матрицы инноваций для семплера Гиббса, заданное как разделенная разделенными запятой парами, состоящая из 'Sigma0' и a PriorMdl.NumSeries-by- PriorMdl.NumSeries положительная определенная числовая матрица. По умолчанию Sigma0 - невязка средняя квадратичная невязка из многомерных наименьших квадратов. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных по PriorMdl.SeriesNames.

Совет

Хорошей практикой является запуск simulate несколько раз с различными начальными значениями параметра. Проверьте, что оценки из каждого запуска сходятся к аналогичным значениям.

Типы данных: double

Выходные аргументы

свернуть все

`Coeff` - Моделируемые коэффициенты модели VAR
числовая матрица

Моделируемые коэффициенты модели VAR, возвращенные как (PriorMdl.NumSeries * k) -by- NumDraws числовая матрица, где k = PriorMdl. NumSeries*PriorMdl. P + PriorMdl. IncludeIntercept + PriorMdl. IncludeTrend + PriorMdl. NumPredictors, которое является количеством коэффициентов в уравнении отклика. Каждый столбец является отдельным рисунком от распределения.

Для рисования j, Коефф (1: k, j) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(1), Коефф ((k + 1): (2* k), j) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(2)и так далее. Для набора индексов, соответствующих уравнению:

Элементы 1 через PriorMdl.NumSeries соответствуют задержке 1 AR коэффициентов переменных отклика, упорядоченных по PriorMdl.SeriesNames.
Элементы PriorMdl.NumSeries + 1 через 2*PriorMdl.NumSeries соответствуют задержке 2 коэффициентов AR переменных отклика, упорядоченных по PriorMdl.SeriesNames.
В целом элементы (q – 1) *PriorMdl. NumSeries + 1 через q*PriorMdl. NumSeries соответствуют задержке q Коэффициенты AR переменных отклика, упорядоченные по PriorMdl.SeriesNames.
Если PriorMdl.IncludeConstant является true, элемент PriorMdl.NumSeries*PriorMdl.P + 1 является моделью постоянной.
Если PriorMdl.IncludeTrend является true, элемент PriorMdl.NumSeries*PriorMdl.P + 2 - линейный коэффициент тренда времени.
Если PriorMdl.NumPredictors > 0, элементы PriorMdl.NumSeries*PriorMdl.P + 3 через k составить вектор коэффициентов регрессии экзогенных переменных.

Этот рисунок показывает структуру Coeff (L, j) для 2-D модели VAR (3), которая содержит постоянный вектор и четыре экзогенных предиктора.

$[\overset{y_{1, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 11} & ϕ_{1, 12} & ϕ_{2, 11} & ϕ_{2, 12} & ϕ_{3, 11} & ϕ_{3, 12} & c_{1} & β_{11} & β_{12} & β_{13} & β_{14} \end{matrix}}} \overset{y_{2, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 21} & ϕ_{1, 22} & ϕ_{2, 21} & ϕ_{2, 22} & ϕ_{3, 21} & ϕ_{3, 22} & c_{2} & β_{21} & β_{22} & β_{23} & β_{24} \end{matrix}}}],$

где

ϕ _qjk является элементом (j, k) матрицы коэффициентов AR q задержки.
c j является моделью, константой в уравнении переменной j отклика.
<reservedrangesplaceholder4> <reservedrangesplaceholder3> <reservedrangesplaceholder2> - коэффициент регрессии внешней переменной u в уравнении переменной ответа j.

`Sigma` - Моделируемые ковариационные матрицы инноваций
массив положительно определенных числовых матриц

Моделируемые инновации ковариационные матрицы, возвращенные как PriorMdl.NumSeries-by- PriorMdl.NumSeries-by- NumDraws массив положительно определенных числовых матриц.

Каждая страница является отдельной ничьей (ковариацией) от распределения. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных по PriorMdl.SeriesNames.

Если PriorMdl является normalbvarm объект, все ковариации в Sigma равны PriorMdl.Covariance.

Ограничения

simulate невозможно получить значения из improper distribution, которая является распределением, плотность которого не интегрируется с 1.

Подробнее о

свернуть все

Байесовский вектор векторной авторегрессии (VAR)

A Bayesian VAR model обрабатывает все коэффициенты и ковариационную матрицу инноваций как случайные переменные в m -мерной, стационарной модели VARX (p). Модель имеет одну из трех форм, описанных в этой таблице.

Модель	Уравнение
VAR (p) редуцированной формы в обозначении разностного уравнения	$y_{t} = Φ_{1} y_{t - 1} + ... + Φ_{p} y_{t - p} + c + δ t + Β x_{t} + ε_{t} .$
Многомерная регрессия	$y_{t} = Z_{t} λ + ε_{t} .$
Матричная регрессия	$y_{t} = Λ^{'} z_{t}^{'} + ε_{t} .$

Для каждого временного t = 1,..., T:

_yt - m -мерный вектор наблюдаемой отклика, где m = numseries.
_Φ1,..._, - p являются m -by m матрицами коэффициентов AR лагов с 1 по p, где p = numlags.
c - вектор m -by-1 констант модели, если IncludeConstant является true.
δ - вектор m -by-1 коэффициентов линейного временного тренда, если IncludeTrend является true.
Β - m -by - r матрица коэффициентов регрессии вектора r -by - 1 наблюдаемых экзогенных предикторов x t, где r = NumPredictors. Все переменные предиктора появляются в каждом уравнении.
$z_{t} = [\begin{matrix} y_{t - 1}^{'} & y_{t - 2}^{'} & \dots & y_{t - p}^{'} & 1 & t & x_{t}^{'} \end{matrix}],$ который является вектором 1-by- (mp + r + 2), и _Z t является m -by- m (mp + r + 2) блочной диагональной матрицей

$[\begin{matrix} z_{t} & 0_{z} & \dots & 0_{z} \\ 0_{z} & z_{t} & \dots & 0_{z} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0_{z} & 0_{z} & 0_{z} & z_{t} \end{matrix}],$
где 0 z является 1-бай- (mp + r + 2) вектором нулей.
$Λ = {[\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}]}^{'}$ , которая является (mp + r + 2) -by m случайной матрицей коэффициентов, и m (mp + r + 2) -by-1 вектор λ = vec (
_εt является m-на-1 вектором случайных, последовательно некоррелированных, многомерных нормальных инноваций с нулевым вектором для среднего и m -by- m матрицы Это предположение подразумевает, что вероятность данных является

$ℓ (Λ, Σ | y, x) = \prod_{t = 1}^{T} f (y_{t}; Λ, Σ, z_{t}),$
где f m - размерная многомерная нормальная плотность со средним <reservedrangesplaceholder3> <reservedrangesplaceholder2> Λ и ковариацией Σ, оценен в <reservedrangesplaceholder1> <reservedrangesplaceholder0>.

Прежде, чем рассмотреть данные, Вы налагаете joint prior distribution предположение на (Λ,Σ), которым управляет распределение π (Λ,Σ). В байесовском анализе распределение параметров обновляется информацией о параметрах, полученных из вероятности данных. Результатом является joint posterior distribution π (Λ,Σ|<reservedrangesplaceholder2>,<reservedrangesplaceholder1>,<reservedrangesplaceholder0>0), где:

Y - T матрица m, содержащая весь ряд ответов _{y t}, t = 1,..., T.
X - T матрица m, содержащая весь экзогенный ряд _{x t}, t = 1,..., T.
Y 0 является p -by - m матрицей предварительных образцов данных, используемых для инициализации модели VAR для оценки.

Совет

Симуляция Монте-Карло подвержена изменениям. Если simulate использует симуляцию Монте-Карло, тогда оценки и выводы могут варьироваться при вызове simulate несколько раз при, казалось бы, эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите начальное число случайных чисел при помощи rng перед вызовом simulate.

Алгоритмы

Если simulate оценивает апостериорное распределение (когда вы поставляете Y) и апостериор аналитически прослеживается, simulate симулирует непосредственно из апостериорной. В противном случае, simulate использует семплер Гиббса, чтобы оценить апостериор.
Этот рисунок показывает, как simulate уменьшает выборку при помощи значений NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные вытяжки из распределения. simulate удаляет белые прямоугольники из выборки. Оставшиеся NumDraws чёрные прямоугольники составляют выборку.
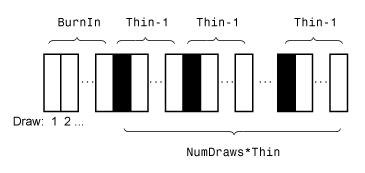
Если PriorMdl является semiconjugatebvarm объект и вы не задаете начальные значения (Coeff0 и Sigma0), simulate выборки из апостериорного распределения путем применения пробоотборника Гиббса.
1. simulate использует значение по умолчанию Sigma0 для, и черпает значение И, из π (и Y, X), полное условное распределение коэффициентов модели VAR.
2. simulate рисует значение И из π (и Y, X), полного условного распределения нововведений ковариации матрицы, при помощи ранее сгенерированного значения И.
3. Функция повторяет шаги 1 и 2 до сходимости. Чтобы оценить сходимость, нарисуйте график трассировки выборки.
Если вы задаете Coeff0, simulate рисует значение И из π (и Y, X), чтобы запустить семплер Гиббса.
simulate не возвращает начальные значения по умолчанию, которые она генерирует.

См. также

Объекты

conjugatebvarm | diffusebvarm | empiricalbvarm | normalbvarm | semiconjugatebvarm

Документация

simulate

Синтаксис

Описание

Примеры

Нарисуйте коэффициенты и инновации Ковариации матрице из предыдущего распределения

Симулируйте параметры из аналитически отслеживаемого апостериорного распределения

Симулируйте параметры из аналитически неразрешимого апостериорного распределения

Симулируйте коэффициенты из модели VARX

Входные параметры

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

Аргументы в виде пар имя-значение

`'NumDraws'` - Количество случайных рисок
`1` (по умолчанию) | положительное целое число

`'Y0'` - Предварительный образец данных отклика
числовая матрица

`'X'` - Данные предиктора
числовая матрица

`'BurnIn'` - Количество розыгрышей для удаления из начала выборки
`0` (по умолчанию) | неотрицательной скаляром

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

`'Coeff0'` - Начальное значение коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

Выходные аргументы

`Coeff` - Моделируемые коэффициенты модели VAR
числовая матрица

`Sigma` - Моделируемые ковариационные матрицы инноваций
массив положительно определенных числовых матриц

Ограничения

Подробнее о

Байесовский вектор векторной авторегрессии (VAR)

Совет

Алгоритмы

См. также

Объекты

Функции

Документация по Econometrics Toolbox

Поддержка

Документация

simulate

Синтаксис

Описание

Примеры

Нарисуйте коэффициенты и инновации Ковариации матрице из предыдущего распределения

Симулируйте параметры из аналитически отслеживаемого апостериорного распределения

Симулируйте параметры из аналитически неразрешимого апостериорного распределения

Симулируйте коэффициенты из модели VARX

Входные параметры

PriorMdl - Предыдущая байесовская модель VAR conjugatebvarm объект модели | semiconjugatebvarm объект модели | diffusebvarm объект модели | normalbvarm объект модели

Y - Наблюдаемый многомерный ряд отклика числовая матрица

Аргументы в виде пар имя-значение

'NumDraws' - Количество случайных рисок 1 (по умолчанию) | положительное целое число

'Y0' - Предварительный образец данных отклика числовая матрица

'X' - Данные предиктора числовая матрица

'BurnIn' - Количество розыгрышей для удаления из начала выборки 0 (по умолчанию) | неотрицательной скаляром

'Thin' - Скорректированный множитель размера выборки 1 (по умолчанию) | положительное целое число

'Coeff0' - Начальное значение коэффициентов модели VAR для дискретизатора Гиббса числовые векторы-столбцы

'Sigma0' - Начальное значение ковариационной матрицы инноваций для семплера Гиббса положительная определенная числовая матрица

Выходные аргументы

Coeff - Моделируемые коэффициенты модели VAR числовая матрица

Sigma - Моделируемые ковариационные матрицы инноваций массив положительно определенных числовых матриц

Ограничения

Подробнее о

Байесовский вектор векторной авторегрессии (VAR)

Совет

Алгоритмы

См. также

Объекты

Функции

Документация по Econometrics Toolbox

Поддержка

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

`'NumDraws'` - Количество случайных рисок
`1` (по умолчанию) | положительное целое число

`'Y0'` - Предварительный образец данных отклика
числовая матрица

`'X'` - Данные предиктора
числовая матрица

`'BurnIn'` - Количество розыгрышей для удаления из начала выборки
`0` (по умолчанию) | неотрицательной скаляром

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

`'Coeff0'` - Начальное значение коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

`Coeff` - Моделируемые коэффициенты модели VAR
числовая матрица

`Sigma` - Моделируемые ковариационные матрицы инноваций
массив положительно определенных числовых матриц