simsmooth

Сглаживание симуляции модели байесовской векторной авторегрессии (VAR)

Синтаксис

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y)

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y,Name,Value)

[CoeffDraws,SigmaDraws,NaNDraws]
= simsmooth(___)

[CoeffDraws,SigmaDraws,NaNDraws,YMean,YStd]
= simsmooth(___)

Описание

simsmooth хорошо подходит для продвинутых приложений, таких как выборочное условное прогнозирование из апостериорного прогнозирующего распределения байесовской модели VAR (p), прогнозирование модели VARX (p), вменение отсутствующего значения и оценка параметра в присутствии отсутствующих значений. Также,simsmooth позволяет вам настроить дискретизатор Гиббса для прогнозирования вне выборки. Для оценки выборочных прогнозов из байесовской модели VAR (p) см. forecast.

пример

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y) возвращает 1000 случайных рисунок векторов коэффициентов λ Coeff и инновации ковариации матрицах, Sigma, полученный из апостериорного распределения, образованного объединением предыдущей байесовской модели VAR (p) PriorMdl и данные отклика Y.

Процедура дискретизации включает шаг увеличения Байесовских данных, который использует фильтр Калмана (см. Алгоритмы). Во время отбора проб, simsmooth заменяет отсутствующие значения без предварительного опредления в Y, обозначенный NaN значений с вмененными значениями.

пример

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y,Name,Value) использует дополнительные опции, заданные одним или несколькими аргументами пары "имя-значение". Для примера можно задать количество случайных рисований из распределения или указать данные отклика предварительного образца.

пример

[CoeffDraws,SigmaDraws,NaNDraws] = simsmooth(___) также возвращает вмененные значения отклика каждого розыгрыша NaNDraws использование любой комбинации входных аргументов в предыдущих синтаксисах.

пример

[CoeffDraws,SigmaDraws,NaNDraws,YMean,YStd] = simsmooth(___) также возвращает среднее YMean и стандартное отклонение YStd апостериорного прогнозирующего распределения дополненных данных.

Примеры

свернуть все

Симулируйте параметры из апостериорного распределения при наличии отсутствующих значений

Открыть Live Script

Когда simulate оценивает апостериорное распределение, из которого можно нарисовать параметры, удаляет все строки в данных, которые содержат по крайней мере одно отсутствующее значение (NaN). Однако simsmooth использует увеличение байесовских данных, чтобы вписать отсутствующие значения, не являющиеся предварительными, во время апостериорной оценки.

Рассмотрим 3-D модель VAR (4) для инфляции в США (INFL), безработица (UNRATE), и федеральные фонды (FEDFUNDS) ставки.

$[\begin{array}{llllllllllllllllllll} {INFL}_{t} \\ {UNRATE}_{t} \\ {FEDFUNDS}_{t} \end{array}] = c + \sum_{j = 1}^{4} Φ_{j} [\begin{array}{llllllllllllllllllll} {INFL}_{t - j} \\ {UNRATE}_{t - j} \\ {FEDFUNDS}_{t - j} \end{array}] + [\begin{array}{cccccccccccccccccccc} ε_{1, t} \\ ε_{2, t} \\ ε_{3, t} \end{array}] .$

Для всех $t$ , $ε_{t}$ - серия независимых 3-D нормальных инноваций со средним значением 0 и ковариацией $Σ$ . Предположим, что слабое сопряженное предшествующее распределение для параметров $({[Φ_{1}, . . ., Φ_{4}, c]}^{'}, Σ)$ .

Загрузка и предварительная обработка данных

Загрузите набор макроэкономических данных США. Рассчитать уровень инфляции и стабилизировать показатели безработицы и федеральных фондов.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);

Несколько серий имеют ведущие NaN значения, потому что их измерения были недоступны одновременно с другими измерениями. Потому что ведущие NaN значения могут влиять на предварительный образец спецификации, удалять все строки, содержащие по крайней мере одно начальное отсутствующее значение.

rmldDataTable = rmmissing(DataTable(:,seriesnames));

Создайте предыдущую модель

Создайте слабую сопряженную предшествующую модель путем определения больших предшествующих отклонений коэффициента. Задайте имена рядов ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Случайное размещение отсутствующих значений в данных

Чтобы проиллюстрировать симуляцию при наличии отсутствующих значений, случайным образом поместите отсутствующие значения в данные после периода предварительного образца.

rng(1)                          % For reproducibility
T = size(rmldDataTable,1);
idxpre = 1:PriorMdl.P;          % Presample period
idxest = (PriorMdl.P + 1):T;    % Estimation period 

nmissing = 20;                  % Simulate at most nmissing missing values
sidx = [randsample(idxest,nmissing,true); randsample(1:numseries,nmissing,true)];
lsidx = sub2ind([T,numseries],sidx(1,:),sidx(2,:));
MissData = table2array(rmldDataTable);
MissData(lsidx) = NaN;
MissDataTable = rmldDataTable;
MissDataTable{:,:} = MissData;

Симулируйте параметры из апостериорной функции

Нарисуйте 1000 наборов параметров из апостериорного распределения путем вызова simsmooth, который оценивает апостериорное распределение параметров, а затем формирует апостериорное прогнозирующее распределение.

[Coeff,Sigma] = simsmooth(PriorMdl,MissDataTable);

Coeff - матрица 39 на 1000 векторов случайным образом нарисованных коэффициентов из апостериорной матрицы. Sigma является массивом 3х3-х1000 случайным образом нарисованных инноваций ковариации матрицах.

По умолчанию simsmooth инициализирует модель VAR при помощи первых четырех наблюдений в данных.

Чтобы связать строки Coeff для коэффициентов получаем сводные данные предыдущего распределения при помощи summarize. В таблице отобразите первый набор случайным образом нарисованных коэффициентов с соответствующими именами.

Summary = summarize(PriorMdl,'off');
table(Coeff(:,1),'RowNames',Summary.CoeffMap)

ans=39×1 table
                      Var1   
                   __________

    AR{1}(1,1)        0.22109
    AR{1}(1,2)       -0.24034
    AR{1}(1,3)       0.093315
    AR{2}(1,1)        0.18329
    AR{2}(1,2)       -0.23178
    AR{2}(1,3)      -0.026301
    AR{3}(1,1)        0.39991
    AR{3}(1,2)        0.41141
    AR{3}(1,3)       0.054702
    AR{4}(1,1)       0.024944
    AR{4}(1,2)       -0.37372
    AR{4}(1,3)     -0.0095642
    Constant(1)       0.21499
    AR{1}(2,1)      -0.073776
    AR{1}(2,2)        0.36086
    AR{1}(2,3)       0.071088
      ⋮

Кроме того, можно создать эмпирическую модель из рисунков и использовать summarize отображение модели путем задания любого параметра отображения.

Отобразите сводные данные апостериорных рисунков как уравнение.

EmpMdl = empiricalbvarm(numseries,numlags,'SeriesNames',seriesnames,...
    'CoeffDraws',Coeff,'SigmaDraws',Sigma);
summarize(EmpMdl,'equation')

                                                                                 VAR Equations                                                                                
           | INFL(-1)  DUNRATE(-1)  DFEDFUNDS(-1)  INFL(-2)  DUNRATE(-2)  DFEDFUNDS(-2)  INFL(-3)  DUNRATE(-3)  DFEDFUNDS(-3)  INFL(-4)  DUNRATE(-4)  DFEDFUNDS(-4)  Constant 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 INFL      |  0.1447     -0.3685        0.1013      0.2974     -0.0959        0.0360      0.4115      0.2244        0.0474      0.0265     -0.2321        0.0030      0.1095  
           | (0.0744)    (0.1314)      (0.0370)    (0.0833)    (0.1509)      (0.0398)    (0.0833)    (0.1440)      (0.0403)    (0.0879)    (0.1301)      (0.0370)    (0.0744) 
 DUNRATE   | -0.0187      0.4445        0.0314      0.0836      0.2372        0.0489     -0.0407     -0.0548       -0.0064      0.0483     -0.1753        0.0027     -0.0597  
           | (0.0447)    (0.0808)      (0.0234)    (0.0514)    (0.0863)      (0.0230)    (0.0507)    (0.0906)      (0.0243)    (0.0514)    (0.0779)      (0.0225)    (0.0466) 
 DFEDFUNDS | -0.2046     -1.1927       -0.2524      0.2864     -0.2282       -0.2657      0.2709     -0.6231        0.0289     -0.0404      0.1043       -0.1236     -0.2952  
           | (0.1530)    (0.2931)      (0.0816)    (0.1832)    (0.3123)      (0.0857)    (0.1736)    (0.3105)      (0.0900)    (0.1866)    (0.2880)      (0.0758)    (0.1684) 
 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.2842   -0.0098     0.1346  
           | (0.0286)  (0.0122)   (0.0464) 
 DUNRATE   | -0.0098    0.1062    -0.1496  
           | (0.0122)  (0.0106)   (0.0296) 
 DFEDFUNDS |  0.1346   -0.1496     1.3187  
           | (0.0464)  (0.0296)   (0.1422)

Смотрите дополненные данные

Открыть Live Script

Рассмотрим 3-D модель VAR (4) моделирования параметров из апостериорного распределения при наличии отсутствующих значений .

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);

Удалите все строки, содержащие начальные отсутствующие значения.

rmldDataTable = rmmissing(DataTable(:,seriesnames));

Создайте слабую сопряженную предшествующую модель. Задайте имена рядов ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Случайным образом поместите отсутствующие значения в данные после периода предварительного образца.

rng(1)                          % For reproducibility
T = size(rmldDataTable,1);
idxpre = 1:PriorMdl.P;          % Presample period
idxest = (PriorMdl.P + 1):T;    % Estimation period 

nmissing = 20;                  % Simulate at most nmissing missing values
sidx = [randsample(idxest,nmissing,true); randsample(1:numseries,nmissing,true)];
lsidx = sub2ind([T,numseries],sidx(1,:),sidx(2,:));
MissData = table2array(rmldDataTable);
MissData(lsidx) = NaN;
MissDataTable = rmldDataTable;
MissDataTable{:,:} = MissData;

Нарисуйте 1000 наборов параметров из апостериорного распределения путем вызова simsmooth. Верните значения, которые симуляция сглаживает для недостающих наблюдений.

[~,~,NaNDraws] = simsmooth(PriorMdl,MissDataTable);

NaNDraws - матрица 19 на 1000 случайным образом нарисованных векторов отклика из апостериорного прогнозирующего распределения. Элементы соответствуют отсутствующим значениям в данных, упорядоченных столбцовым поиском. Для примера, NaNDraws(3,1) - первый случайным образом нарисованный вмененный ответ третьего отсутствующего значения в данных. Найдите соответствующее значение в данных.

[idxi,idxj] = find(ismissing(MissDataTable),3);
responsename = seriesnames(idxj(end))

responsename = 
"INFL"

observationtime = MissDataTable.Time(idxi(end))

observationtime = datetime
   Q3-65

Постройте график эмпирического распределения вмененных значений уровня инфляции во время Q3-65.

histogram(NaNDraws(3,:))
title('Q3-65 Inflation Rate Empirical Distribution')

Figure contains an axes. The axes with title Q3-65 Inflation Rate Empirical Distribution contains an object of type histogram.

Настройте опции выборки Simulation Smooter

Открыть Live Script

Загрузите набор макроэкономических данных США. Вычислите уровень инфляции, стабилизируйте ставки безработицы и федеральных фондов и удалите недостающие значения (данные включают только ведущие отсутствующие значения).

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте слабую сопряженную предшествующую модель. Задайте имена рядов ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Симулируйте 5000 коэффициентов и инновационных ковариационных матриц из апостериорного распределения. Задайте период горения 1000 и коэффициент утончения 5.

rng(1); % For reproducibility
[Coeff,Sigma] = simsmooth(PriorMdl,rmDataTable{:,seriesnames},...
    'NumDraws',5000,'BurnIn',1000,'Thin',5);

Coeff является матрицей коэффициентов 39 на 5000 и Sigma массив инновационных ковариационных матриц 3 на 3 на 5000. Оба Coeff и Sigma случайным образом вытягиваются из апостериорного распределения.

Задайте начальные значения коэффициента для Simulation Smooter

Открыть Live Script

Рассмотрим 3-D модель VAR (4) моделирования параметров из апостериорного распределения при наличии отсутствующих значений. В этом случае примите, что предыдущая модель является полунъюгатной.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте полуконъюгатную предшествующую модель. Задайте имена рядов ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'ModelType','semiconjugate',...
    'SeriesNames',seriesnames);

Чтобы получить начальные значения для коэффициентов, рассмотрите коэффициенты из модели VAR, подобранной к первым 30 наблюдениям.

Задайте наборы индексов, которые разделяют данные на четыре набора:

Длина p = 4 период инициализации для динамического компонента модели
$n_{0}$ = 30 наблюдений для оценки VAR начальных значений коэффициента
Длина p = 4 период инициализации для динамического компонента байесовской модели VAR
Оставление $n_{1}$ наблюдения для оценки апостериорной функции

T = size(rmDataTable);
n0 = 30;
idxpre0 = 1:PriorMdl.P;
idxest0 = (idxpre0(end) + 1):(idxpre0(end) + 1 + n0);
idxpre1 = (idxest0(end) + 1 - PriorMdl.P):idxest0(end);
idxest1 = (idxest0(end) + 1):T;
n1 = numel(idxest1);

Получите начальные значения коэффициентов путем подбора модели VAR к первым 34 наблюдениям. Используйте первые четыре наблюдения в качестве предварительной выборки.

Mdl0 = varm(PriorMdl.NumSeries,PriorMdl.P);
EstMdl0 = estimate(Mdl0,rmDataTable{idxest0,seriesnames},'Y0',rmDataTable{idxpre0,seriesnames});

estimate возвращает объект модели, содержащий оценки коэффициентов AR в матричной форме и константы в векторе. Функции Bayesian VAR требуют начальных значений коэффициентов в векторе. Форматируйте начальные значения коэффициентов.

Coeff0 = [EstMdl0.AR{:} EstMdl0.Constant].';
Coeff0 = Coeff0(:);

Симулируйте 1000 коэффициентов и ковариаций матриц из апостериорного распределения. Задайте оставшиеся наблюдения, из которых можно оценить апостериорные. Инициализируйте модель VAR, задав последние четыре наблюдения в предыдущей выборке оценки в качестве предварительной выборки и задайте вектор начального коэффициента, чтобы инициализировать апостериорную выборку.

rng(1); % For reproducibility
[Coeff,Sigma] = simsmooth(PriorMdl,rmDataTable{idxest1,seriesnames},...
    'Y0',rmDataTable{idxpre1,seriesnames},'Coeff0',Coeff0);

Coeff - матрица коэффициентов и Sigma 39 на 1000 массив инновационных ковариационных матриц 3 на 3 на 1000. Оба Coeff и Sigma случайным образом вытягиваются из апостериорного распределения.

Прогнозные отклики от апостериорного прогнозирующего распределения

Открыть Live Script

Загрузка и предварительная обработка данных

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте предыдущую модель

Создайте слабую сопряженную предшествующую модель. Задайте имена рядов ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Прогнозирование ответов с использованием forecast

Непосредственно прогнозируется два года (восемь четвертей) наблюдений от апостериорного прогнозирующего распределения. forecast оценивает апостериорное распределение параметров, а затем формирует апостериорное прогнозирующее распределение.

rng(1); % For reproducibility
numperiods = 8;
YF = forecast(PriorMdl,numperiods,rmDataTable{:,seriesnames});

YF - матрица прогнозируемых ответов 8 на 3.

Постройте график прогнозируемых откликов.

fh = rmDataTable.Time(end) + calquarters(1:8);
for j = 1:PriorMdl.NumSeries
    subplot(3,1,j)
    plot(rmDataTable.Time(end - 20:end),rmDataTable{end - 20:end,seriesnames(j)},'r',...
        [rmDataTable.Time(end) fh],[rmDataTable{end,seriesnames(j)}; YF(:,j)],'b');
    legend("Observed","Forecasted",'Location','NorthWest')
    title(seriesnames(j))
end

Figure contains 3 axes. Axes 1 with title INFL contains 2 objects of type line. These objects represent Observed, Forecasted. Axes 2 with title DUNRATE contains 2 objects of type line. These objects represent Observed, Forecasted. Axes 3 with title DFEDFUNDS contains 2 objects of type line. These objects represent Observed, Forecasted.

Прогнозирование ответов с использованием simsmooth

Сконфигурируйте набор данных для получения прогнозов от simsmooth путем конкатенации numperiods-by- numseries timetable отсутствующих значений до конца набора.

fTT = array2timetable(NaN(numperiods,numseries),'RowTimes',fh,...
    'VariableNames',seriesnames);
frmDataTable = [rmDataTable(:,seriesnames); fTT];
tail(frmDataTable)

ans=8×3 timetable
    Time     INFL    DUNRATE    DFEDFUNDS
    _____    ____    _______    _________

    Q2-09    NaN       NaN         NaN   
    Q3-09    NaN       NaN         NaN   
    Q4-09    NaN       NaN         NaN   
    Q1-10    NaN       NaN         NaN   
    Q2-10    NaN       NaN         NaN   
    Q3-10    NaN       NaN         NaN   
    Q4-10    NaN       NaN         NaN   
    Q1-11    NaN       NaN         NaN

Прогнозируйте модель VAR с помощью simsmooth. Как forecast, simsmooth оценивает апостериорное распределение, поэтому это требует предыдущей модели и данных. Укажите данные, содержащие конечные NaNс.

[~,~,~,YMean] = simsmooth(PriorMdl,frmDataTable);

YMean почти равен frmDataTable, за этими исключениями:

YMean исключает строки, соответствующие периоду предварительного образца frmDataTable(1:4,:).
Если frmDataTable(j,k) является NaN, YMean(j,k) - среднее значение апостериорного прогнозирующего распределения отклика k во время j.

Составьте расписание из YMean.

YMeanTT = array2timetable(YMean,'RowTimes',frmDataTable.Time((PriorMdl.P + 1):end),...
    'VariableNames',seriesnames);

Постройте график прогнозируемых откликов.

for j = 1:PriorMdl.NumSeries
    subplot(3,1,j)
    plot(YMeanTT.Time((end - 20 - numperiods):(end - numperiods)),YMeanTT{(end - 20 - numperiods):(end - numperiods),j},'r',...
        YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,j},'b');
        legend("Observed","Forecasted",'Location','NorthWest')
    title(seriesnames(j))
end

Оценка условных прогнозов

Открыть Live Script

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте слабую сопряженную предшествующую модель. Задайте имена рядов ответов.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Условное прогнозирование происходит, когда значения отклика известны или гипотезированы в прогнозном горизонте, и неизвестные значения прогнозируются обусловленными известными значениями. Предположим, что уровень безработицы меняется (DUNRATE) остается на одной процентной точке через двухлетний прогнозный горизонт.

Сконфигурируйте набор данных для получения прогнозов от simsmooth путем конкатенации numperiods-by- numseries timetable отсутствующих значений до конца набора. Для изменения уровня безработицы замените отсутствующие значения вектором с таковыми.

rng(1); % For reproducibility
numperiods = 8;
fh = rmDataTable.Time(end) + calquarters(1:8);

fTT = array2timetable(NaN(numperiods,numseries),'RowTimes',fh,...
    'VariableNames',seriesnames);

frmDataTable = [rmDataTable(:,seriesnames); fTT];
frmDataTable.DUNRATE((end - numperiods + 1):end) = ones(numperiods,1);
tail(frmDataTable)

ans=8×3 timetable
    Time     INFL    DUNRATE    DFEDFUNDS
    _____    ____    _______    _________

    Q2-09    NaN        1          NaN   
    Q3-09    NaN        1          NaN   
    Q4-09    NaN        1          NaN   
    Q1-10    NaN        1          NaN   
    Q2-10    NaN        1          NaN   
    Q3-10    NaN        1          NaN   
    Q4-10    NaN        1          NaN   
    Q1-11    NaN        1          NaN

Получить прогнозы по уровню инфляции и федеральным фондам изменить ставки, учитывая, что изменение уровня безработицы является единичным для всего горизонта.

[~,~,~,YMean] = simsmooth(PriorMdl,frmDataTable);

YMean почти равен frmDataTable, за этими исключениями:

YMean исключает строки, соответствующие периоду предварительного образца frmDataTable(1:4,:).
Если frmDataTable(j,k) является NaN, YMean(j,k) - среднее значение апостериорного прогнозирующего распределения отклика k во время j.

Составьте расписание из YMean.

YMeanTT = array2timetable(YMean,'RowTimes',frmDataTable.Time((PriorMdl.P + 1):end),...
    'VariableNames',seriesnames);

Постройте график прогнозируемых откликов.

for j = 1:PriorMdl.NumSeries
    subplot(3,1,j)
    plot(YMeanTT.Time((end - 20 - numperiods):(end - numperiods)),YMeanTT{(end - 20 - numperiods):(end - numperiods),j},'r',...
        YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,j},'b');
        legend("Observed","Forecasted",'Location','NorthWest')
    title(seriesnames(j))
end

Прогнозная модель VARX

Открыть Live Script

Рассмотрим 2-D модель VARX (1) для реального ВВП США (RGDP) и инвестиции (GCE) тарифы, которые лечат личное потребление (PCEC) скорость как экзогенная:

$[\begin{array}{llllllllllllllllllll} {RGDP}_{t} \\ {GCE}_{t} \end{array}] = c + Φ [\begin{array}{llllllllllllllllllll} {RGDP}_{t - 1} \\ {GCE}_{t - 1} \end{array}] + {PCEC}_{t} β + ε_{t} .$

Для всех $t$ , $ε_{t}$ - серия независимых 2-D нормальных инноваций со средним значением 0 и ковариацией $Σ$ . Примите следующие предыдущие распределения:

${[\begin{array}{c} Φ & c & β \end{array}]}^{'} | Σ \sim Ν_{4 \times 2} (Μ, V, Σ)$ , где M является матрицей средств 4 на 2 и $V$ - матрица шкалы между коэффициентами 4 на 4. Эквивалентно, $vec ({[\begin{array}{c} Φ & c & β \end{array}]}^{'}) | Σ \sim Ν_{8} (vec (Μ), Σ \otimes V)$ .
$Σ \sim I n v e r s e W i s h a r t (Ω, ν),$ где И - матрица шкалы 2 на 2, $ν$ - степени свободы.

Загрузите набор макроэкономических данных США. Вычислите реальный показатель ВВП, инвестиций и личного потребления. Удалите все отсутствующие значения из получившейся серии.

load Data_USEconModel
DataTable.RGDP = DataTable.GDP./DataTable.GDPDEF;
seriesnames = ["PCEC"; "RGDP"; "GCE"];
rates = varfun(@price2ret,DataTable,'InputVariables',seriesnames);
rates = rmmissing(rates);
rates.Properties.VariableNames = seriesnames;

Создайте сопряженную предшествующую модель для параметров модели 2-D VARX (1).

numseries = 2;
numlags = 1;
numpredictors = 1;
PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,...
    'SeriesNames',seriesnames(2:end));

Создайте наборы индексов, которые разделяют данные на оценочные и прогнозные выборки. Укажите горизонт прогноза на два года.

T = size(rates,1);
numperiods = 8;
idxest = 1:(T - numperiods); % Includes presample
idxf = (T - numperiods + 1):T;
idxtot = [idxest idxf];

Симуляция сглаживает прогнозы путем ввода отсутствующих значений. Поэтому создайте набор данных, который содержит отсутствующие значения для откликов в горизонте прогноза.

missingrates = rates;
missingrates{idxf,PriorMdl.SeriesNames} = nan(numperiods,PriorMdl.NumSeries);

Прогнозные отклики в прогнозном горизонте. Задайте наблюдения presample и данные экзогенного предиктора. Верните стандартные отклонения апостериорного прогнозирующего распределения.

rng(1) % For reproducibility
[~,~,~,YMean,YStd] = simsmooth(PriorMdl,missingrates{:,PriorMdl.SeriesNames},...
    'X',missingrates{:,seriesnames(1)});

Составьте расписание из YMean.

YMeanTT = array2timetable(YMean,'RowTimes',rates.Time((PriorMdl.P + 1):end),...
    'VariableNames',PriorMdl.SeriesNames);

Постройте график прогнозируемых откликов.

for j = 1:PriorMdl.NumSeries
    subplot(PriorMdl.NumSeries,1,j)
    plot(rates.Time((end - 20):end),rates{(end - 20):end,PriorMdl.SeriesNames(j)},'r',...
        YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,PriorMdl.SeriesNames(j)},'b');
        legend("Observed","Forecasted",'Location','NorthWest')
    title(PriorMdl.SeriesNames(j))
end

Figure contains 2 axes. Axes 1 with title RGDP contains 2 objects of type line. These objects represent Observed, Forecasted. Axes 2 with title GCE contains 2 objects of type line. These objects represent Observed, Forecasted.

Входные параметры

свернуть все

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

Предыдущая модель Bayesian VAR, заданная как объект модели в этой таблице.

Объект модели	Описание
`conjugatebvarm`	Зависимая, матричная-нормальная-обратная-Wishart сопряженная модель, возвращенная `bayesvarm`, `conjugatebvarm`, или `estimate`
`semiconjugatebvarm`	Независимая, нормальная-обратная-Wishart полусредняя предыдущая модель, возвращенная `bayesvarm` или `semiconjugatebvarm`
`diffusebvarm`	Диффузная предыдущая модель, возвращенная `bayesvarm` или `diffusebvarm`
`normalbvarm`	Нормальная сопряженная модель с фиксированной инновационной ковариационной матрицей, возвращенной `bayesvarm`, `normalbvarm`, или `estimate`

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

Наблюдался многомерный ряд отклика, на который simsmooth подходит для модели, заданной как numobs-by- numseries числовая матрица.

numobs - размер выборки. numseries - количество переменных отклика (PriorMdl.NumSeries).

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. Столбцы соответствуют отдельным переменным отклика.

NaN значения в Y указать отсутствующие наблюдения. simsmooth заменяет отсутствующие значения без предварительной выборки на условные (см. NaNDraws) в рамках процесса отбора проб.

Y представляет продолжение предизмерительного ряда откликов Y0.

Совет

Получение numperiods не выборочные прогнозы, конкатенация numperiods-by- numseries матрица NaNс до конца Y. simsmooth возвращает прогнозы и стандартные отклонения в соответствующих элементах YMean и YStd, соответственно. Для примера:
```
numperiods = 8;
Y = [Y; NaN(numperiods,PriorMdl.NumSeries)];
```
Для получения прогнозов, обусловленных наблюдаемыми (или гипотезированными) значениями в прогнозном горизонте, соедините numperiods-by- numseries матрица NaNs и наблюдаемые или гипотезированные значения до конца Y. Для примера в 2-D системе получите одноэтапный прогноз переменной отклика 1, учитывая, что переменная отклика 2 равна 0,5, путем определения
```
Y = [Y; [NaN 0.5]];
```

Типы данных: double

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: 'Y0',Y0,'X',X задает предварительные данные отклика Y0 для инициализации модели VAR для апостериорной симуляции и данных предиктора X для компонента экзогенной регрессии.

`'Y0'` - Предварительный образец данных отклика
числовая матрица

Предварительный образец данных отклика для инициализации модели VAR для симуляции, заданный как разделенная разделенными запятой парами, состоящая из 'Y0' и a numpreobs-by- numseries числовая матрица. numpreobs - количество предварительных наблюдений.

Строки соответствуют предварительным образцам наблюдений, а последняя строка содержит последнее наблюдение. Y0 должно иметь по крайней мере PriorMdl.P строки. Если вы поставляете больше строк, чем нужно, simsmooth использует последние PriorMdl.P только наблюдения.

Столбцы должны соответствовать ряду ответов в Y.

По умолчанию, simsmooth использует Y(1:PriorMdl.P,:) в качестве предварительного примера наблюдений, а затем оценивает апостериорное использование Y((PriorMdl.P + 1):end,:). Это действие уменьшает эффективный размер выборки. Количество строк выходов YMean и YStd является size(Y,1) – PriorMdl.P. Если Y0 содержит, по крайней мере, один NaN, simsmooth выдает ошибку.

Типы данных: double

`'X'` - Данные предиктора
числовая матрица

Данные предиктора для компонента экзогенной регрессии в модели, заданные как разделенная разделенными запятой парами, состоящая из 'X' и a numobs-by- PriorMdl.NumPredictors числовая матрица.

Строки соответствуют наблюдениям, а последняя строка содержит последнее наблюдение. simsmooth не использует регрессионный компонент в предварительном образце периода. X должно иметь, по крайней мере, столько наблюдений, сколько наблюдений, используемых после периода предварительного образца.

Если вы задаете Y0, затем X должно иметь по крайней мере numobs строки (см. Y).
В противном случае X должно иметь по крайней мере numobs – PriorMdl.P наблюдения для расчета удаления предварительного образца.

В любом случае, если вы поставляете больше строк, чем необходимо, simsmooth использует только последние наблюдения.

Столбцы соответствуют отдельным переменным предиктора. Все переменные предиктора присутствуют в регрессионном компоненте каждого уравнения отклика.

Если X содержит, по крайней мере, один NaN, simsmooth выдает ошибку.

Типы данных: double

`'NumDraws'` - Количество случайных рисок
`1` (по умолчанию) | положительное целое число

Количество случайных рисований из распределений, заданное как разделенная разделенными запятой парами, состоящая из 'NumDraws' и положительное целое число.

Пример: 'NumDraws',1e7

Типы данных: double

`'BurnIn'` - Количество розыгрышей для удаления из начала выборки
`0` (по умолчанию) | неотрицательной скаляром

Количество розыгрышей для удаления из начала выборки для уменьшения переходных эффектов, заданное как разделенная разделенными запятой парами, состоящая из 'BurnIn' и неотрицательный скаляр. Для получения дополнительной информации о том, как simsmooth уменьшает полную выборку, см. Алгоритмы.

Совет

Чтобы помочь вам указать соответствующий размер периода горения:

Определите степень переходного поведения в выборке путем определения 'BurnIn',0.
Симулируйте несколько тысяч наблюдений при помощи simsmooth.
Нарисуйте графики трассировки.

Пример: 'BurnIn',0

Типы данных: double

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

Скорректированный множитель размера выборки, заданный как разделенная разделенными запятой парами, состоящая из 'Thin' и положительное целое число.

Фактический размер выборки BurnIn + NumDraws*Thin. После отбрасывания горения, simsmooth отбрасывает каждый Thin – 1 рисует, а затем сохраняет следующий розыгрыш. Для получения дополнительной информации о том, как simsmooth уменьшает полную выборку, см. Алгоритмы.

Совет

Чтобы уменьшить потенциальную большую последовательную корреляцию в выборке или уменьшить потребление памяти рисунков, сохраненных в PriorMdl, задайте большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

`'Coeff0'` - Начальное значение коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

Начальное значение коэффициентов модели VAR для семплера Гиббса, заданное как разделенная разделенными запятой парами, состоящая из 'Coeff0' и числовой вектор-столбец с (Mdl.NumSeries * k) -by- NumDraws элементы, где k = Mdl. NumSeries*Mdl. P + Mdl. IncludeIntercept + Mdl. IncludeTrend + Mdl. NumPredictors, которое является количеством коэффициентов в уравнении отклика. Для получения дополнительной информации о структуре Coeff0, см. выход CoeffDraws.

По умолчанию Coeff0 - многомерная оценка методом наименьших квадратов.

Совет

Чтобы задать Coeff0:
1. Установите отдельные переменные для начальных значений каждой матрицы коэффициентов и вектора.
2. Горизонтально конкатенируйте все средства коэффициентов в этом порядке:
  
  $C o e f f = [\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}] .$
3. Векторизация транспонирования средней матрицы коэффициентов.
  Coeff0 = Coeff.'; Coeff0 = Coeff0(:);
Хорошей практикой является запуск simsmooth несколько раз с различными начальными значениями параметра. Проверьте, что оценки из каждого запуска сходятся к аналогичным значениям.

Типы данных: double

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

Начальное значение ковариационной матрицы инноваций для семплера Гиббса, заданное как разделенная разделенными запятой парами, состоящая из 'Sigma0' и a PriorMdl.NumSeries-by- PriorMdl.NumSeries положительная определенная числовая матрица. По умолчанию Sigma0 - невязка средняя квадратичная невязка из многомерных наименьших квадратов. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных по Mdl.SeriesNames.

Совет

Хорошей практикой является запуск simsmooth несколько раз с различными начальными значениями параметра. Проверьте, что оценки из каждого запуска сходятся к аналогичным значениям.

Типы данных: double

Выходные аргументы

свернуть все

`CoeffDraws` - Моделируемые коэффициенты модели VAR
числовая матрица

Моделируемые коэффициенты модели VAR, возвращенные как (PriorMdl.NumSeries * k) -by- NumDraws числовая матрица, где k = PriorMdl. NumSeries*PriorMdl. P + PriorMdl. IncludeIntercept + PriorMdl. IncludeTrend + PriorMdl. NumPredictors, которое является количеством коэффициентов в уравнении отклика.

Каждый столбец является последовательным рисунком (вектор коэффициентов) из апостериорного распределения.

Для рисования j, CoeffDraws (1: k, j) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(1), Коефф ((k + 1): (2* k), j) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(2)и так далее. Для набора индексов, соответствующих уравнению:

Элементы 1 через PriorMdl.NumSeries соответствуют задержке 1 AR коэффициентов переменных отклика, упорядоченных по PriorMdl.SeriesNames.
Элементы PriorMdl.NumSeries + 1 через 2*PriorMdl.NumSeries соответствуют задержке 2 коэффициентов AR переменных отклика, упорядоченных по PriorMdl.SeriesNames.
В целом элементы (q – 1) *PriorMdl. NumSeries + 1 через q*PriorMdl. NumSeries соответствуют задержке q Коэффициенты AR переменных отклика, упорядоченные по PriorMdl.SeriesNames.
Если PriorMdl.IncludeConstant является true, элемент PriorMdl.NumSeries*PriorMdl.P + 1 является моделью постоянной.
Если Mdl.IncludeTrend является true, элемент PriorMdl.NumSeries*PriorMdl.P + 2 - линейный коэффициент тренда времени.
Если PriorMdl.NumPredictors > 0, элементы PriorMdl.NumSeries*PriorMdl.P + 3 через k составить вектор коэффициентов регрессии экзогенных переменных.

Этот рисунок показывает структуру CoeffDraws (:, j) для 2-D модели VAR (3), которая содержит постоянный вектор и четыре экзогенных предиктора.

$[\overset{y_{1, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 11} & ϕ_{1, 12} & ϕ_{2, 11} & ϕ_{2, 12} & ϕ_{3, 11} & ϕ_{3, 12} & c_{1} & β_{11} & β_{12} & β_{13} & β_{14} \end{matrix}}} \overset{y_{2, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 21} & ϕ_{1, 22} & ϕ_{2, 21} & ϕ_{2, 22} & ϕ_{3, 21} & ϕ_{3, 22} & c_{2} & β_{21} & β_{22} & β_{23} & β_{24} \end{matrix}}}],$

где

ϕ _qjk является элементом (j, k) матрицы коэффициентов AR q задержки.
c j является моделью, константой в уравнении переменной j отклика.
<reservedrangesplaceholder4> <reservedrangesplaceholder3> <reservedrangesplaceholder2> - коэффициент регрессии внешней переменной u в уравнении переменной ответа j.

`SigmaDraws` - Моделируемые ковариационные матрицы инноваций
массив положительно определенных числовых матриц

Моделируемые инновации ковариационные матрицы, возвращенные как PriorMdl.NumSeries-by- PriorMdl.NumSeries-by- NumDraws массив положительно определенных числовых матриц.

Каждая страница является последовательным получением (ковариацией) от апостериорного распределения. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных по PriorMdl.SeriesNames.

Если PriorMdl является normalbvarm объект, все ковариации в SigmaDraws равны PriorMdl.Covariance.

`NaNDraws` - Расчеты по отсутствующим данным отклика
числовая матрица

Вменения для отсутствующих данных отклика, возвращенные как numNaNs-by- NumDraws числовая матрица, где numNaNs = sum(isNaN(Y)), количество NaNs в данных отклика.

Каждый столбец является последовательным ничьим (вектором выражений отклика) из апостериорного прогнозирующего распределения.

Каждая строка соответствует NaN в Y. simsmooth определяет порядок строк при помощи столбцового поиска. Например, предположим Y является следующей матрицей.

Y = [  1  NaN;...
      NaN  2 ;...
      NaN  5 ;...
        7  8];

Здесь, NaNDraws является 3-байт- NumDraws матрица. Для рисования j, NaNDraws (1, j) содержит вмененное значение переменной отклика PriorMdl.SeriesNames(1) в 2 времени NaNDraws (2, j) содержит вмененное значение переменной отклика PriorMdl.SeriesNames(1) в момент 3 и NaNDraws (3, j) содержит вмененное значение переменной отклика PriorMdl.SeriesNames(2) в момент времени 1.

`YMean` - Дополненные данные отклика
числовая матрица

Дополненные данные отклика, возвращенные как numobs-by- PriorMdl.NumSeries числовая матрица. YMean равен не предварительному фрагменту данных отклика Y, но simsmooth заменяет каждый NaN с соответствующим средним значением апостериорного прогнозирующего распределения (YMean содержит ноль отсутствующих значений).

`YStd` - Стандартные отклонения апостериорного прогнозирующего распределения
числовая матрица

Стандартные отклонения апостериорного прогнозирующего распределения вмененных ответов, возвращенные как numobs-by- PriorMdl.NumSeries числовая матрица. Размерности YStd и YMean соответствуют.

Отсутствующие значения в данных отклика Y, которые соответствуют вмененным значениям в YMean, иметь ненулевое стандартное отклонение. Стандартные отклонения, соответствующие немиссирующим данным отклика, равны 0.

Подробнее о

свернуть все

Байесовский вектор векторной авторегрессии (VAR)

A Bayesian VAR model обрабатывает все коэффициенты и ковариационную матрицу инноваций как случайные переменные в m -мерной, стационарной модели VARX (p). Модель имеет одну из трех форм, описанных в этой таблице.

Модель	Уравнение
VAR (p) редуцированной формы в обозначении разностного уравнения	$y_{t} = Φ_{1} y_{t - 1} + ... + Φ_{p} y_{t - p} + c + δ t + Β x_{t} + ε_{t} .$
Многомерная регрессия	$y_{t} = Z_{t} λ + ε_{t} .$
Матричная регрессия	$y_{t} = Λ^{'} z_{t}^{'} + ε_{t} .$

Для каждого временного t = 1,..., T:

_yt - m -мерный вектор наблюдаемой отклика, где m = numseries.
_Φ1,..._, - p являются m -by m матрицами коэффициентов AR лагов с 1 по p, где p = numlags.
c - вектор m -by-1 констант модели, если IncludeConstant является true.
δ - вектор m -by-1 коэффициентов линейного временного тренда, если IncludeTrend является true.
Β - m -by - r матрица коэффициентов регрессии вектора r -by - 1 наблюдаемых экзогенных предикторов x t, где r = NumPredictors. Все переменные предиктора появляются в каждом уравнении.
$z_{t} = [\begin{matrix} y_{t - 1}^{'} & y_{t - 2}^{'} & \dots & y_{t - p}^{'} & 1 & t & x_{t}^{'} \end{matrix}],$ который является вектором 1-by- (mp + r + 2), и _Z t является m -by- m (mp + r + 2) блочной диагональной матрицей

$[\begin{matrix} z_{t} & 0_{z} & \dots & 0_{z} \\ 0_{z} & z_{t} & \dots & 0_{z} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0_{z} & 0_{z} & 0_{z} & z_{t} \end{matrix}],$
где 0 z является 1-бай- (mp + r + 2) вектором нулей.
$Λ = {[\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}]}^{'}$ , которая является (mp + r + 2) -by m случайной матрицей коэффициентов, и m (mp + r + 2) -by-1 вектор λ = vec (
_εt является m-на-1 вектором случайных, последовательно некоррелированных, многомерных нормальных инноваций с нулевым вектором для среднего и m -by- m матрицы Это предположение подразумевает, что вероятность данных является

$ℓ (Λ, Σ | y, x) = \prod_{t = 1}^{T} f (y_{t}; Λ, Σ, z_{t}),$
где f m - размерная многомерная нормальная плотность со средним <reservedrangesplaceholder3> <reservedrangesplaceholder2> Λ и ковариацией Σ, оценен в <reservedrangesplaceholder1> <reservedrangesplaceholder0>.

Прежде, чем рассмотреть данные, Вы налагаете joint prior distribution предположение на (Λ,Σ), которым управляет распределение π (Λ,Σ). В байесовском анализе распределение параметров обновляется информацией о параметрах, полученных из вероятности данных. Результатом является joint posterior distribution π (Λ,Σ|<reservedrangesplaceholder2>,<reservedrangesplaceholder1>,<reservedrangesplaceholder0>0), где:

Y - T матрица m, содержащая весь ряд ответов _{y t}, t = 1,..., T.
X - T матрица m, содержащая весь экзогенный ряд _{x t}, t = 1,..., T.
Y 0 является p -by - m матрицей предварительных образцов данных, используемых для инициализации модели VAR для оценки.

Апостериорное прогнозирующее распределение

posterior predictive distribution следующего ВАРА Bayesian (<reservedrangesplaceholder13>) модель π (Yf | Y, X) распределение следующих τ будущих переменных ответа после заключительного наблюдения в _{выборке} оценки _Yf = [<reservedrangesplaceholder6> <reservedrangesplaceholder5> +1, <reservedrangesplaceholder4> <reservedrangesplaceholder3> +2..., <reservedrangesplaceholder2> <reservedrangesplaceholder1> + τ], учитывая следующее, маргинализованный по Λ и Σ:

Предварительная выборка и оценка данных отклика на выборку Y
Коэффициенты И
Инновации ковариации матрица
Оценка и будущая выборка экзогенных данных X

Символически,

$π (Y_{f} | Y, X) = \int π (Y_{f} | Y, X, Λ, Σ) π (Λ, Σ | Y, X) d Λ d Σ .$

Семплер Гиббса с байесовским увеличением данных

Это Gibbs sampler with Bayesian data augmentation является методом выборки Монте-Карло цепи Маркова, который берётся из апостериорного распределения параметров и незабываемых данных отклика, учитывая наблюдаемые данные.

Рассмотрим следующие наборы индексов:

I = {(i, j) | i = 1,..., m + τ, j = 1,..., m + τ}, вселенная, содержащая все пары индексов (i, j) данных, не являющихся предварительными образцами, и горизонт прогноза. Y (I) представляет все данные отклика, не являющиеся предварительными образцами, включая любые заполнители (NaN значения) для отсутствующих наблюдений и ненаблюдаемых значений в прогнозном горизонте.
U = {(i, j) ∈ <reservedrangesplaceholder6> | Y (i, j) отсутствует или ненаблюдаемый}, набор соответствия пар индекса пропавшим без вести или ненаблюдаемым данным ответа. Y (U) является набором заполнителей, и Y (U^c) - набор наблюдаемых данных.

simsmooth моделирует из апостериорного распределения отсутствующих данных отклика, коэффициентов и ковариационной матрицы инноваций $π (Y (U), Λ, Σ | Y (U^{c}), X)$ следуя этому пробоотборнику Гиббса.

Создайте модель пространства состояний без ошибок наблюдения путем применения заданной структуры VAR (p) к уравнениям состояния. Примените начальные значения параметров⁽⁰⁾ и⁽⁰⁾ (Coeff0 и Sigma0). Получившаяся модель является условной апостериорной π прогнозирующего распределения (Y (U) |Λ⁽⁰⁾,Σ⁽⁰⁾, Y (U^c), X).
Во время итерации j:
1. Симулируйте отсутствующие данные Y (U)^(j) от π (Y (U) |^(j-1),Σ^(j-1), Y (U^c), X). Чтобы выполнить это действие, simsmooth использует симуляцию модели пространства состояний более гладкую (см. simsmooth функция ssm объект модели). simsmooth хранит Y (U)^(j) в выход NaNDraws.
2. Составьте дополненный набор данных Y (I)^(j) = Y (<reservedrangesplaceholder0>)^(j) ∪ Y (U^c).
3. Нарисуйте коэффициенты^(j) и инновационную ковариационную матрицу^(j) из условной следующей модели Bayesian VAR с увеличенными данными π (Λ,Σ | Y (<reservedrangesplaceholder0>)^(j), X). simsmooth хранит^(j) и^(j) в выходах CoeffDraws и SigmaDraws, соответственно.
Среднее и стандартное отклонение следующего прогнозирующего распределения π (Y (<reservedrangesplaceholder1>) | Λ,Σ, Y (U^c), X) - среднее и стандартное отклонение ряда розыгрышей {Y (U)^(j)}. simsmooth сохраняет статистику в выходах YMean и YStd.

После удаления периода горения (Burnin) и утончение выборки (Thin), simsmooth сохраняет оставшийся набор рисований и вычисляет из него апостериорную статистику.

Совет

Симуляция Монте-Карло подвержена изменениям. Если simsmooth использует симуляцию Монте-Карло, тогда оценки и выводы могут варьироваться при вызове simsmooth несколько раз при, казалось бы, эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите начальное число случайных чисел при помощи rng перед вызовом simsmooth.

Алгоритмы

Этот рисунок показывает, как simsmooth уменьшает выборку при помощи значений NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные вытяжки из распределения. simsmooth удаляет белые прямоугольники из выборки. Оставшиеся NumDraws чёрные прямоугольники составляют выборку.
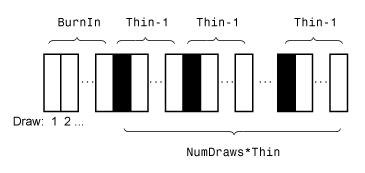
simsmooth не возвращает начальные значения по умолчанию, которые она генерирует.

Ссылки

[1] Литтерман, Роберт Б. «Прогнозирование с байесовскими векторными авторегрессиями: пятилетний опыт». Журнал деловой и экономической статистики 4, № 1 (январь 1986 года): 25-38. https://doi.org/10.2307/1391384.

См. также

Объекты

conjugatebvarm | diffusebvarm | empiricalbvarm | normalbvarm | semiconjugatebvarm

Документация

simsmooth

Синтаксис

Описание

Примеры

Симулируйте параметры из апостериорного распределения при наличии отсутствующих значений

Смотрите дополненные данные

Настройте опции выборки Simulation Smooter

Задайте начальные значения коэффициента для Simulation Smooter

Прогнозные отклики от апостериорного прогнозирующего распределения

Оценка условных прогнозов

Прогнозная модель VARX

Входные параметры

PriorMdl - Предыдущая байесовская модель VAR conjugatebvarm объект модели | semiconjugatebvarm объект модели | diffusebvarm объект модели | normalbvarm объект модели

Y - Наблюдаемый многомерный ряд отклика числовая матрица

Аргументы в виде пар имя-значение

'Y0' - Предварительный образец данных отклика числовая матрица

'X' - Данные предиктора числовая матрица

'NumDraws' - Количество случайных рисок 1 (по умолчанию) | положительное целое число

'BurnIn' - Количество розыгрышей для удаления из начала выборки 0 (по умолчанию) | неотрицательной скаляром

'Thin' - Скорректированный множитель размера выборки 1 (по умолчанию) | положительное целое число

'Coeff0' - Начальное значение коэффициентов модели VAR для дискретизатора Гиббса числовые векторы-столбцы

'Sigma0' - Начальное значение ковариационной матрицы инноваций для семплера Гиббса положительная определенная числовая матрица

Выходные аргументы

CoeffDraws - Моделируемые коэффициенты модели VAR числовая матрица

SigmaDraws - Моделируемые ковариационные матрицы инноваций массив положительно определенных числовых матриц

NaNDraws - Расчеты по отсутствующим данным отклика числовая матрица

YMean - Дополненные данные отклика числовая матрица

YStd - Стандартные отклонения апостериорного прогнозирующего распределения числовая матрица

Подробнее о

Байесовский вектор векторной авторегрессии (VAR)

Апостериорное прогнозирующее распределение

Семплер Гиббса с байесовским увеличением данных

Совет

Алгоритмы

Ссылки

См. также

Объекты

Функции

Документация по Econometrics Toolbox

Поддержка

`PriorMdl` - Предыдущая байесовская модель VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` - Наблюдаемый многомерный ряд отклика
числовая матрица

`'Y0'` - Предварительный образец данных отклика
числовая матрица

`'X'` - Данные предиктора
числовая матрица

`'NumDraws'` - Количество случайных рисок
`1` (по умолчанию) | положительное целое число

`'BurnIn'` - Количество розыгрышей для удаления из начала выборки
`0` (по умолчанию) | неотрицательной скаляром

`'Thin'` - Скорректированный множитель размера выборки
`1` (по умолчанию) | положительное целое число

`'Coeff0'` - Начальное значение коэффициентов модели VAR для дискретизатора Гиббса
числовые векторы-столбцы

`'Sigma0'` - Начальное значение ковариационной матрицы инноваций для семплера Гиббса
положительная определенная числовая матрица

`CoeffDraws` - Моделируемые коэффициенты модели VAR
числовая матрица

`SigmaDraws` - Моделируемые ковариационные матрицы инноваций
массив положительно определенных числовых матриц

`NaNDraws` - Расчеты по отсутствующим данным отклика
числовая матрица

`YMean` - Дополненные данные отклика
числовая матрица

`YStd` - Стандартные отклонения апостериорного прогнозирующего распределения
числовая матрица