Сравнительные тесты модели

Доступные тесты

Основной целью выбора модели является выбор самой скупой модели, которая адекватно подходит для ваших данных. Три асимптотически эквивалентных теста сравнивают ограниченную модель (нулевую модель) с неограниченной моделью (альтернативная модель), подобранной к тем же данным:

Тест коэффициента правдоподобия (LR)
Тест множителя Лагранжа (LM)
Тест Вальда (W)

Для модели с θ параметров рассмотрим ограничение $r (θ) = 0,$ что удовлетворяется нулевой моделью. Например, рассмотрите проверку нулевой гипотезы $θ = θ_{0} .$ Функция ограничения для этого теста

$r (θ) = θ - θ_{0} .$

Тесты LR, LM и Wald подходят к проблеме сравнения подгонки ограниченной модели с неограниченной моделью по-разному. Для заданного набора данных позвольте $l (θ_{0}^{M L E})$ обозначает функцию логарифмической правдоподобности, оцененную в максимальной оценке правдоподобия (MLE) ограниченной (null) модели. Давайте $l (θ_{A}^{M L E})$ обозначает функцию логарифмической правдоподобности, оцененную в MLE неограниченной (альтернативной) модели. Следующий рисунок иллюстрирует обоснование каждого теста.

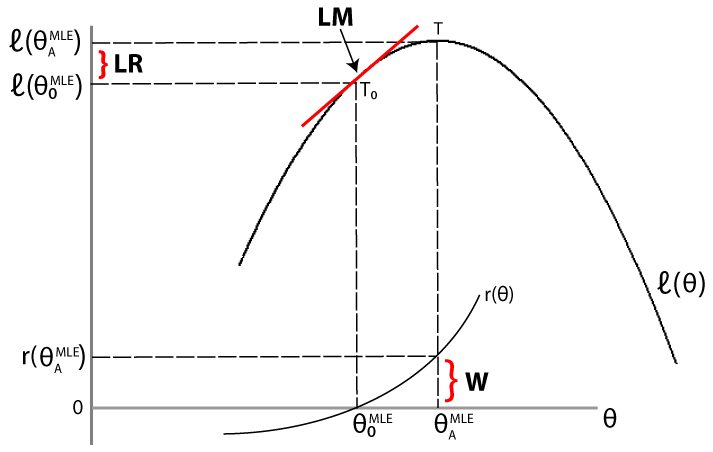
Тест коэффициента вероятности. Если ограниченная модель адекватна, то различие между максимальными целевыми функциями, $l (θ_{A}^{M L E}) - l (θ_{0}^{M L E}),$ не должен существенно отличаться от нуля.
Тест множителя Лагранжа. Если ограниченная модель адекватна, то наклон тангенса функции логарифмической правдоподобности в ограниченной MLE (обозначенной _T0 на рисунке) не должен существенно отличаться от нуля (что является наклоном тангенса функции логарифмической правдоподобности в неограниченной MLE, обозначенной T).
Тест Уолда. Если ограниченная модель является адекватной, то функция ограничения, оцененная в неограниченном MLE, не должна значительно отличаться от нуля (что является значением функции ограничения в ограниченном MLE).

Три теста асимптотически эквивалентны. В значении null статистика тестов LR, LM и Wald распределена как $χ^{2}$ со степенями свободы, равными количеству ограничений. Если тестовая статистическая величина превышает критическое значение теста (эквивалентно, p-значение меньше или равно уровню значимости), нулевая гипотеза отклоняется. То есть ограниченная модель отклоняется в пользу неограниченной модели.

Выбор среди тестов LR, LM и Wald в значительной степени определяется вычислительными затратами:

Чтобы провести тест коэффициента вероятности, необходимо оценить как ограниченную, так и неограниченную модели.
Чтобы провести тест множителя Лагранжа, вам нужно только оценить ограниченную модель (но тест требует оценки дисперсионно-ковариационной матрицы).
Чтобы провести тест Уолда, вам нужно только оценить неограниченную модель (но тест требует оценки дисперсионно-ковариационной матрицы).

При всем равном, тест LR часто является предпочтительным выбором для сравнения вложенных моделей. Econometrics Toolbox™ имеет функциональность для всех трех тестов.

Тест коэффициента правдоподобия

Можно провести тест коэффициента вероятности, используя lratiotest. Требуемые входы:

Значение максимальной неограниченной логарифмической правдоподобности, $l (θ_{A}^{M L E})$
Значение максимальной ограниченной логарифмической правдоподобности, $l (θ_{0}^{M L E})$
Количество ограничений (степени свободы)

Учитывая эти входы, статистическая характеристика теста отношения вероятностей

$G^{2} = 2 \times [l (θ_{A}^{M L E}) - l (θ_{0}^{M L E})] .$

При оценке условных моделей среднего и отклонения (использование arima, garch, egarch, или gjr), можно вернуть значение целевой функции логарифмической правдоподобности как необязательный выходной аргумент estimate или infer. Для многомерных моделей временных рядов можно получить значение целевой функции логарифмической правдоподобности с помощью estimate.

Тест множителя Лагранжа

Необходимые входы для проведения теста множителя Лагранжа:

Градиент неограниченной вероятности, оцененный в ограниченных MLE (счетах), S
Дисперсионно-ковариационная матрица для неограниченных параметров, оцененных в ограниченных MLE, V

Учитывая эти входы, тестовая статистика LM

$L M = S^{'} V S .$

Можно провести тест LM с помощью lmtest. Конкретным примером LM-теста является ARCH-тест Engle, который можно провести с помощью archtest.

Тест Уолда

Необходимые входы для проведения теста Вальда:

Функция ограничения, оцененная в неограниченном MLE, r
Якобиан функции ограничения, оцененный в неограниченных MLE, R
Дисперсионно-ковариационная матрица для неограниченных параметров, оцененных в неограниченных MLE, V

Учитывая эти входы, тестовая статистика для теста Уолда

$W = r^{'} {(R V R^{'})}^{- 1} r .$

Можно провести тест Уолда, используя waldtest.

Совет

Часто можно вычислить якобиан функции ограничения аналитически. Или, если у вас есть Symbolic Math Toolbox™, можно использовать функцию jacobian.

Ковариация матрицы

Для оценки дисперсионно-ковариационной матрицы существует несколько распространенных методов, включая:

Векторное произведение градиентов (ОПГ). Предположим G что это матрица градиентов функции логарифмической правдоподобности. Если у Вашего набора данных есть N наблюдения, и в неограниченной вероятности есть m параметры, то G - матрица <reservedrangesplaceholder1> × <reservedrangesplaceholder0>.
Матрица ${(G^{'} G)}^{- 1}$ - оценка OPG дисперсионно-ковариационной матрицы.
Для arima, garch, egarch, и gjr модели, estimate метод возвращает оценку OPG дисперсионно-ковариационной матрицы.
Обратный отрицательный Гессиан (INH). Учитывая функцию логарифмической правдоподобности $l (θ),$ ковариационная оценка INH имеет элементы

$cov (i, j) = {(- \frac{\partial^{2} l (θ)}{\partial θ_{i} \partial θ_{j}})}^{- 1} .$
Функция оценки для многомерных моделей, estimate, возвращает ожидаемую дисперсионно-ковариационную матрицу Гессия.

Совет

Если у вас есть Symbolic Math Toolbox, можно использовать jacobian дважды вычислить матрицу Гессия для функции логарифмической правдоподобности.

Документация