Мультипликативные спецификации модели ARIMA

Сезонная модель ARIMA без постоянного термина

В этом примере показано, как использовать arima задать мультипликативную сезонную модель ARIMA (для ежемесячных данных) без постоянного члена.

Задайте мультипликативную сезонную модель ARIMA без постоянного члена,

$(1 - ϕ_{1} L) (1 - Φ_{12} L^{12}) (1 - L)^{1} (1 - L^{12}) y_{t} = (1 + θ_{1} L) (1 + Θ_{12} L^{12}) ε_{t},$

где инновационное распределение является Гауссовым с постоянным отклонением. Вот, $(1 - L)^{1}$ является несезональным оператором дифференцирования первой степени и $(1 - L^{12})$ - сезонный оператор дифференцирования первой степени с периодичностью 12.

Mdl = arima('Constant',0,'ARLags',1,'SARLags',12,'D',1,...
            'Seasonality',12,'MALags',1,'SMALags',12)

Mdl = 
  arima with properties:

     Description: "ARIMA(1,1,1) Model Seasonally Integrated with Seasonal AR(12) and MA(12) (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 26
               D: 1
               Q: 13
        Constant: 0
              AR: {NaN} at lag [1]
             SAR: {NaN} at lag [12]
              MA: {NaN} at lag [1]
             SMA: {NaN} at lag [12]
     Seasonality: 12
            Beta: [1×0]
        Variance: NaN

Область аргумента пары "имя-значение" ARLags задает задержку, соответствующую несезонному коэффициенту AR, $ϕ_{1}$ . SARLags задает задержку, соответствующую сезонному коэффициенту AR, здесь при задержке 12. Аналогичным образом заданы несезонные и сезонные коэффициенты MA. D задает степень несезонного интегрирования. Seasonality определяет периодичность временных рядов, например Seasonality = 12 указывает ежемесячные данные. Начиная с Seasonality больше 0, степень сезонного интегрирования $D_{s}$ это единица.

Всякий раз, когда вы включаете сезонные AR или MA полиномы (сигнализируется путем определения SAR или SMA) в спецификации модели, arima включает их мультипликационно. arima устанавливает свойство P равно p + D + $p_{s}$ + с (здесь 1 + 1 + 12 + 12 = 26). Точно так же arima устанавливает свойство Q равно q + $q_{s}$ (здесь 1 + 12 = 13).

Отобразите значение SAR:

Mdl.SAR

ans=1×12 cell array
  Columns 1 through 8

    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}    {[0]}

  Columns 9 through 12

    {[0]}    {[0]}    {[0]}    {[NaN]}

The SAR массив ячеек возвращает 12 элементов, как задано SARLags. arima устанавливает коэффициенты при промежуточных лагах равными нулю, чтобы поддерживать согласованность с индексацией массива ячеек MATLAB ®. Поэтому единственный ненулевой коэффициент соответствует задержке 12 .

Все другие свойства Mdl являются NaN- значение, указывающее, что соответствующие параметры модели являются оценочными, или можно задать их значение с помощью записи через точку.

Сезонная модель ARIMA с известными значениями параметров

Открыть Live Script

В этом примере показано, как задать мультипликативную сезонную модель ARIMA (для квартальных данных) с известными значениями параметров. Можно использовать такую полностью заданную модель в качестве входов для simulate или forecast.

Задайте мультипликативную сезонную модель ARIMA

$(1 - . 5 L) (1 + 0.7 L^{4}) (1 - L)^{1} (1 - L^{4}) y_{t} = (1 + . 3 L) (1 - . 2 L^{4}) ε_{t},$

где инновационное распределение является Гауссовым с постоянным отклонением 0,15. Вот, $(1 - L)^{1}$ является несезонным оператором дифференцирования и $(1 - L^{4})$ - сезонный оператор дифференцирования первой степени с периодичностью 4.

Mdl = arima('Constant',0,'AR',0.5,'D',1,'MA',0.3,...
    'Seasonality',4,'SAR',-0.7,'SARLags',4,...
    'SMA',-0.2,'SMALags',4,'Variance',0.15)

Mdl = 
  arima with properties:

     Description: "ARIMA(1,1,1) Model Seasonally Integrated with Seasonal AR(4) and MA(4) (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 10
               D: 1
               Q: 5
        Constant: 0
              AR: {0.5} at lag [1]
             SAR: {-0.7} at lag [4]
              MA: {0.3} at lag [1]
             SMA: {-0.2} at lag [4]
     Seasonality: 4
            Beta: [1×0]
        Variance: 0.15

Выход задает несезонные и сезонные коэффициенты AR с противоположными знаками по сравнению с полиномами задержки. Это согласуется с формой разностного уравнения модели. Этот выход задает лаги сезонных коэффициентов AR и MA, используя SARLags и SMALags, соответственно. D задает степень несезонного интегрирования. Seasonality = 4 задает ежеквартальные данные с одной степенью сезонного интегрирования.

Все значения параметров заданы, то есть никакое свойство объекта не NaN-значен.

Задайте мультипликативную модель ARIMA с помощью приложения Econometric Modeler

В командной строке откройте приложение Econometric Modeler.
```
econometricModeler
```
Также откройте приложение из галереи Apps (см. Econometric Modeler).
На панели Time Series выберите временные ряды отклика, к которому будет соответствовать модель.
На вкладке Econometric Modeler, в разделе Models, щелкните стреле, чтобы отобразить галерею моделей.
В ARMA/ARIMA Models разделе галереи нажмите SARIMA. Чтобы создать модели SARIMAX, смотрите Спецификации Модели ARIMAX.
Откроется диалоговое окно SARIMA Model Parameters.
Задайте структуру задержки. Используйте вкладку Lag Order, чтобы определить SARIMA (p, D, q) × (_ps, _Ds, _qs) модель s, которая включает:
- Все последовательные лаги от 1 до их соответствующих порядков в несезонных полиномах
- Лаги, которые все являются последовательными кратными периоду (s), в сезонных полиномах
- Многочлен сезонного интегрирования s -степень
Используйте вкладку Lag Vector для гибкости, чтобы задать определенные лаги для всех полиномов. Для получения дополнительной информации смотрите Определение полиномов оператора задержки в интерактивном режиме. Независимо от используемой вкладки, можно проверить форму модели, осмотрев уравнение в Model Equation разделе.

Для примера рассмотрим эту модель SARIMA (2,1,1) × (_2,1,1) 12.

$(1 - ϕ_{1} L - ϕ_{2} L^{2}) (1 - Φ_{12} L^{12} - Φ_{24} L^{24}) (1 - L) (1 - L^{12}) y_{t} = c + (1 + θ_{1} L) (1 + Θ_{12} L^{12}) ε_{t},$

где _εt - серия IID Гауссовых инноваций.

Модель включает все последовательные задержки AR и MA от 1 до их соответствующих порядков. Кроме того, лаги полиномов РСА и SMA являются последовательными кратными периоду от 12 до их соответствующих значений времени 12 заданного порядка. Поэтому используйте вкладку Lag Order, чтобы задать модель.

В Nonseasonal разделе:
1. Установите Degree of Integration значение 1.
2. Установите Autoregressive Order значение 2.
3. Установите Moving Average Order значение 1.
В Seasonal разделе:
1. Установите Period значение 12.
2. Установите Autoregressive Order значение 2. Этот вход задает включение РСА лагов 12 и 24 (то есть первых и вторых множителей значения Period).
3. Установите Moving Average Order значение 1. Этот вход задает включение задержки 12 SMA (то есть первого кратного значению Period).
4. Установите флажок Include Seasonal Difference.
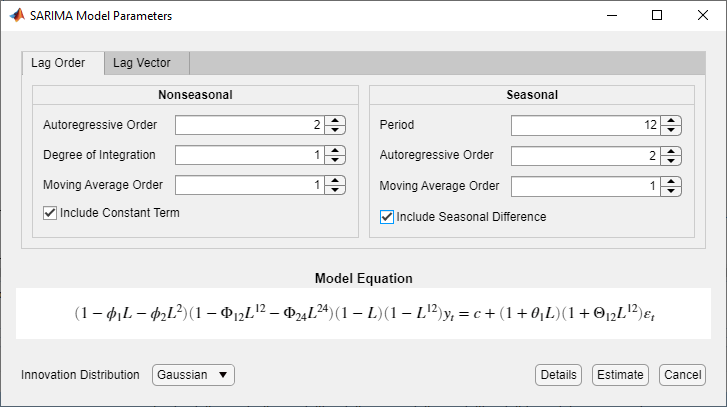
Проверьте, что уравнение в разделе Model Equation соответствует вашей модели.

Чтобы исключить константу из модели и указать, что нововведения являются Гауссовыми, выполните предыдущие шаги и снимите флажок Include Constant Term.
Чтобы задать t -распределенные инновации, следуйте предыдущим шагам и нажмите кнопку Innovation Distribution, а затем выберите t.

Для другого примера рассмотрим эту модель SARIMA (12,1,1) × (_2,1,1) 12.

$(1 - ϕ_{1} L - ϕ_{12} L^{12}) (1 - Φ_{24} L^{24}) (1 - L) (1 - L^{12}) y_{t} = c + (1 + θ_{1} L) (1 + Θ_{12} L^{12}) ε_{t} .$

Модель не включает последовательные AR-лаги, и лаги полинома РСА не являются последовательными кратными периоду. Поэтому используйте вкладку Lag Vector, чтобы задать эту модель:

В диалоговом окне SARIMA Model Parameters щелкните вкладку Lag Vector.
В Nonseasonal разделе:
1. Установите Degree of Integration значение 1.
2. Установите Autoregressive Lags значение 1 12.
3. Установите Moving Average Lags значение 1.
В Seasonal разделе:
1. Установите Seasonality значение 12. Приложение включает 12-градусный сезонный полином интегрирования.
2. Установите Autoregressive Lags значение 24. Этот вход определяет включение задержки РСА 24. Вход не зависит от значения в Seasonality поле.
3. Установите Moving Average Lags значение 12. Этот вход задает включение задержки 12 SMA. Вход не зависит от значения в Seasonality поле.
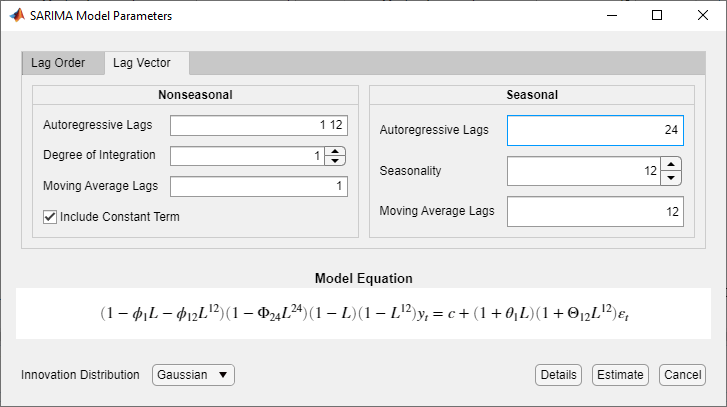
Проверьте, что уравнение в разделе Model Equation соответствует вашей модели.

После того, как вы задаете модель, кликните Estimate, чтобы оценить все неизвестные параметры в модели.

Документация