Функции хеджирования

Введение

Хеджирование - это инвестиция, направленная на снижение риска неблагоприятного изменения цен в активе. Financial Instruments Toolbox™ предлагает две функции для оценки фундаментального компромисса хеджирования, hedgeopt и hedgeslf.

Первая функция, hedgeopt, решает наиболее общую задачу хеджирования. Он выделяет оптимальный хеджирование, чтобы удовлетворить любой из двух целей:

Минимизируйте затраты на хеджирование портфеля с учетом набора целевых чувствительности.
Минимизируйте чувствительность портфеля для данного набора максимальных целевых затрат.

hedgeopt позволяет инвесторам изменять распределение портфеля между инструментами в соответствии с любой из целей. Задача приведена как ограниченный линейный метод наименьших квадратов задача. Для получения дополнительной информации о hedgeopt, см. Хеджирование с хеджевтом.

Вторая функция, hedgeslf, пытается выделить самофинансируемое хеджирование среди портфеля инструментов. В частности, hedgeslf пытается сохранить постоянное значение портфеля в соответствии со снижением чувствительности портфеля (то есть, восстановленный портфель хеджируется против рыночных движений и наиболее близок к самофинансированию). Если hedgeslf не может найти хеджирование с самофинансированием, оно восстанавливает баланс портфеля, чтобы минимизировать общую чувствительность портфеля. Для получения дополнительной информации о hedgeslf, см. Самофинансирование хеджирования с помощью hedgeslf.

Примеры в этом разделе рассматривают меры чувствительности к дельте, гамме и веге. В этом тулбоксе, когда вы работаете с производными по процентным ставкам, дельта - это мера чувствительности к цене сдвигов в форвардной кривой выражения, гамма - это мера чувствительности к дельте сдвигов в форвардной кривой выражения, а вега - это мера чувствительности к ценам сдвигов в процессе волатильности. Посмотрите bdtsens или hjmsens для получения дополнительной информации об расчете чувствительности для производных по процентным ставкам.

Для экзотических опций капитала базисным инструментом является цена акций вместо кривого форвардного выражения. Таким образом, дельта теперь представляет собой меру чувствительности к ценам сдвигов в цене акций, гамма - меру чувствительности к дельте сдвигов в цене акций, а вега - меру чувствительности к ценам сдвигов в волатильности акций. Посмотрите crrsens, eqpsens, ittsens, или sttsens для получения дополнительной информации об расчете чувствительности для производных капитала.

Для примеров, показывающих расчет чувствительности для производных на основе процентных ставок, смотрите Вычислительные Чувствительности Инструмента. Аналогичным образом, для примеров, показывающих расчет чувствительности для экзотических опций капитала, смотрите Вычисление Чувствительности Инструмента Капитала.

Примечание

Чувствительности к дельте, гамме и веге, которые вычисляет тулбокс, являются чувствительностью к доллару.

Хеджирование с `hedgeopt`

Примечание

Числовые результаты в этом разделе отображаются в MATLAB^® формат банка. Несмотря на то, что вычисления выполняются с двойной точностью с плавающей точностью, отображаются только два десятичных знака.

Чтобы проиллюстрировать механизм хеджирования, рассмотрите портфель HJMInstSet полученный из файла примера deriv.mat. Портфель состоит из восьми инструментов: двух облигаций, одной опции на облигации, одной ноты с фиксированной ставкой, одной ноты с плавающей ставкой, одной прописной буквы, одного этажа и одного свопа.

Обе функции хеджирования требуют некоторых общих входов, включая текущие портфельные активы (распределения) и матрицу чувствительности инструмента. Чтобы создать эти входы, загрузите портфолио примера в память

load deriv.mat;

вычисление цены и чувствительности

[Delta, Gamma, Vega, Price] = hjmsens(HJMTree, HJMInstSet);

Warning: Not all cash flows are aligned with the tree. Result will
be approximated.

и извлеките текущие портфельные холдинги.

Holdings = instget(HJMInstSet, 'FieldName', 'Quantity');

Для удобства поместите измерения чувствительности дельты, гаммы и веги в матрицу чувствительности.

Sensitivities = [Delta Gamma Vega];

Каждая строка Sensitivities матрица связана с другим инструментом в портфолио, и каждый столбец с другой мерой чувствительности.

Обобщение информации о портфеле

disp([Price  Holdings  Sensitivities])

 98.72       100.00       -272.65       1029.90       0.00
 97.53        50.00       -347.43       1622.69      -0.04
  0.05       -50.00         -8.08        643.40      34.07
 98.72        80.00       -272.65       1029.90       0.00
100.55         8.00         -1.04          3.31          0
  6.28        30.00        294.97       6852.56      93.69
  0.05        40.00        -47.16       8459.99      93.69
  3.69        10.00       -282.05       1059.68       0.00

Первый столбец выше - это долларовый модуль цена каждого инструмента, второй - владения каждого инструмента (количество удерживаемых или количество контрактов), а третий, четвертый и пятый столбцы - это дельта доллара, гамма и чувствительность веги, соответственно.

Текущие чувствительности портфеля являются взвешенным средним значением инструментов в портфеле.

TargetSens  = Holdings' * Sensitivities

TargetSens =

     -61910.22     788946.21       4852.91

Ведение существующих распределений

Чтобы проиллюстрировать использование hedgeoptпредположим, что вы хотите сохранить свой существующий портфель. Первая форма hedgeopt минимизирует стоимость хеджирования портфеля с учетом набора целевых чувствительности. Если вы хотите сохранить свой существующий состав портфеля и воздействие, вы должны быть в состоянии сделать это, не тратя никаких денег. Чтобы проверить это, установите чувствительность цели к текущим чувствительности.

FixedInd = [1 2 3 4 5 6 7 8];
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,Holdings, FixedInd, [], [], TargetSens)

Holdings =

        100.00
         50.00
        -50.00
         80.00
          8.00
         30.00
         40.00
         10.00


Sens =

     -61910.22     788946.21       4852.91


Cost =

             0


Quantity =

  Columns 1 through 6

        100.00         50.00        -50.00         80.00          8.00         30.00

  Columns 7 through 8

         40.00         10.00

Состав портфеля и чувствительность не меняются, а стоимость, связанная с ничего не делая, равна нулю. Стоимость определяется как изменение значения портфеля. Это число не может быть меньше нуля, потому что стоимость ребалансирования определяется как неотрицательное число.

Если Value0 и Value1 представление стоимости портфеля до и после ребалансировки, соответственно, нулевая стоимость также может быть проверена путем сравнения значений портфеля.

Value0 = Holdings' * Price

Value0 =

     23674.62

Value1 = Quantity * Price

Value1 =

     23674.62

Частично хеджированный портфель

Основываясь на примере ведения существующих распределений, предположим, что вы хотите знать стоимость, чтобы достичь общей чувствительности портфеля к доллару [-23000 -3300 3000], разрешая торговать только инструментами 2, 3 и 6 (удерживая позиции инструментов 1, 4, 5, 7 и 8 фиксированными). Чтобы найти стоимость, сначала установите целевую долларовую чувствительность портфеля.

TargetSens = [-23000 -3300 3000];

Затем укажите инструменты, которые будут фиксированы.

FixedInd = [1 4 5 7 8];

Наконец, позвоните hedgeopt

[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... 
Holdings, FixedInd, [], [], TargetSens);

и снова исследуйте результаты.

Sens =

     -23000.00      -3300.00       3000.00

Cost =

      19174.02

Quantity' =

        100.00
       -141.03
        137.26
         80.00
          8.00
        -57.96
         40.00
         10.00

Пересчет Value1, значение портфеля после ребаланса.

Value1 = Quantity * Price

Value1 =

      4500.60

Как и ожидалось, стоимость, $19174,02, является различием между Value0 и Value1, $23674.62 — $4500.60. Изменены только положения в инструментах 2, 3 и 6.

Полностью хеджированный портфолио

Пример в Частично Хеджированном Портфолио иллюстрирует частичное хеджирование, но, пожалуй, самый интересный случай включает в себя стоимость, связанную с полностью хеджированным портфолио (одновременная дельта, гамма и вегетативность). В этом случае установите целевую чувствительность к вектору-строке 0 с и вызова hedgeopt снова. В следующем примере используются данные из Hedging with hedgeopt.

TargetSens = [0 0 0];
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price, ... 
Holdings, FixedInd, [], [], TargetSens);

Изучение выходов показывает, что вы получили полностью хеджированный портфель

Sens =

         -0.00          -0.00          -0.00

но за счет более 20 000 долларов.

Cost =

      23055.90

Должности, необходимые для достижения полностью хеджированного портфеля

Quantity' =

        100.00
       -182.36
        -19.55
         80.00
          8.00
        -32.97
         40.00
         10.00

привести к новому значению портфеля

Value1 = Quantity * Price

Value1 =

      618.72

Минимизация чувствительности портфеля

Примеры в Fully Hedged Portfolio иллюстрируют, как использовать hedgeopt определить минимальную стоимость хеджирования портфеля с учетом набора целевых чувствительности. В этих примерах целевые чувствительности портфеля рассматриваются как ограничения равенства в процессе оптимизации. Вы говорите hedgeopt какие чувствительности вы хотите, и это говорит вам, что это будет стоить, чтобы получить эти чувствительности.

Связанная с этим проблема заключается в минимизации чувствительности портфеля для данного набора максимальных целевых затрат. Для этой цели целевые затраты рассматриваются как ограничения неравенства в процессе оптимизации. Вы говорите hedgeopt больше всего вы готовы потратить на изоляцию своего портфеля, и это говорит вам о наименьших чувствительности портфеля, которые вы можете получить за свои деньги.

Чтобы проиллюстрировать это использование hedgeopt, вычислите чувствительность портфеля доллара на всей границе затрат. Из предыдущих примеров вы знаете, что траты ничего не наследуют существующий портфель, в то время как траты $23 055,90 полностью хеджируют портфель.

Предположим, например, что вы готовы потратить целых 50 000 долларов и хотите увидеть, какая чувствительность портфеля будет возникать вдоль границы затрат. Предположим, что те же инструменты являются фиксированными и что стоимость границы оценивается от 0 до 50 000 долл. США с шагами в 1000 долл. США.

MaxCost = [0:1000:50000];

Теперь позвоните hedgeopt.

[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price, ... 
Holdings, FixedInd, [], MaxCost);

С помощью этих данных можно построить график требуемых затрат на хеджирование по сравнению с доступными средствами (сумма, которую вы готовы потратить)

plot(MaxCost/1000, Cost/1000, 'red'), grid
xlabel('Funds Available for Rebalancing ($1000''s)')
ylabel('Actual Rebalancing Cost ($1000''s)')
title ('Rebalancing Cost Profile')

Профиль балансировки затрат

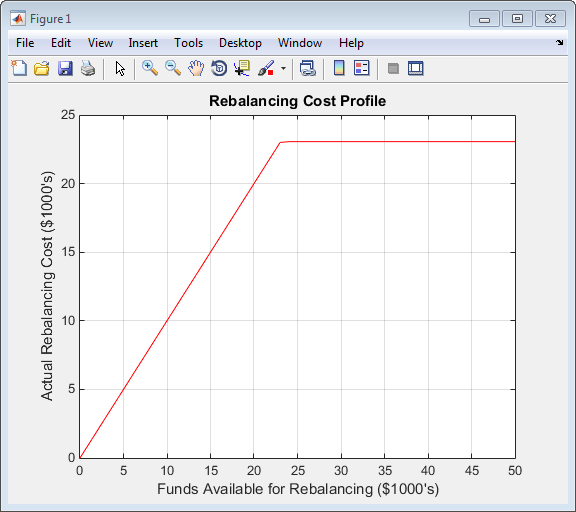
и чувствительность портфеля в долларах по сравнению с имеющимися средствами.

figure
plot(MaxCost/1000, Sens(:,1), '-red')
hold('on')
plot(MaxCost/1000, Sens(:,2), '-.black')
plot(MaxCost/1000, Sens(:,3), '--blue')
grid
xlabel('Funds Available for Rebalancing ($1000''s)')
ylabel('Delta, Gamma, and Vega Portfolio Dollar Sensitivities')
title ('Portfolio Sensitivities Profile')
legend('Delta', 'Gamma', 'Vega', 0)

Средства, доступные для перерасчета

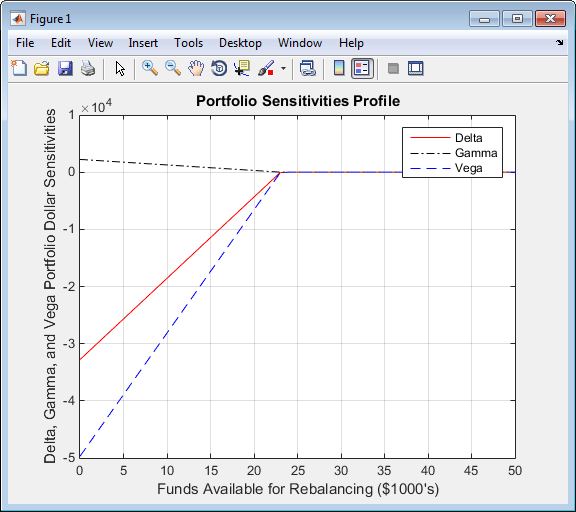
Самофинансирующиеся хеджирования с `hedgeslf`

Данные «Профиль затрат на перерасчет и имеющиеся средства для перерасчета» указывают на отсутствие выгод, поскольку доступные средства для хеджирования превышают 23 055,90 долл. США, что является точкой максимальных расходов, необходимых для получения одновременной дельты, гамма-нейтралитета и вегетарианской нейтральности. Вы также можете найти эту точку дельта, гамма, и вега нейтралитета используя hedgeslf.

[Sens, Value1, Quantity] = hedgeslf(Sensitivities, Price,... 
Holdings, FixedInd);

Подобно hedgeopt, hedgeslf возвращает чувствительности портфеля в долларах США и количества инструментов (восстановленные запасы). Однако, напротив, второй выходной параметр hedgeslf - значение ребалансированного портфеля, из которого можно вычислить стоимость ребалансирования путем вычитания.

Value0 - Value1

ans =

      23055.90

В этом примере портфель явно не является самофинансированием, поэтому hedgeslf находит оптимальное решение, необходимое для получения нулевой чувствительности.

По сути, существует третий синтаксис вызова, доступный для hedgeopt непосредственно связано с результатами, показанными выше для hedgeslf. Предположим, вместо непосредственного определения средств, доступных для ребалансировки (наибольшее количество денег, которые вы готовы потратить), вы хотите просто указать число точек вдоль границы затрат. Этот вызов на hedgeopt отбирает пробу границы стоимости в 10 одинаково разнесенных точках между точкой минимальной стоимости (и потенциально максимальной экспозиции) и точкой минимальной экспозиции (и максимальной стоимости).

[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... 
Holdings, FixedInd, 10)

Sens =
     -32784.46       2231.83     -49694.33
     -29141.74       1983.85     -44172.74
     -25499.02       1735.87     -38651.14
     -21856.30       1487.89     -33129.55
     -18213.59       1239.91     -27607.96
     -14570.87        991.93     -22086.37
     -10928.15        743.94     -16564.78
      -7285.43        495.96     -11043.18
      -3642.72        247.98      -5521.59
          0.00         -0.00          0.00

Cost =
          0.00
       2561.77
       5123.53
       7685.30
      10247.07
      12808.83
      15370.60
      17932.37
      20494.14
      23055.90

Теперь постройте график этих данных.

figure
plot(Cost/1000, Sens(:,1), '-red')
hold('on')
plot(Cost/1000, Sens(:,2), '-.black')
plot(Cost/1000, Sens(:,3), '--blue')
grid
xlabel('Rebalancing Cost ($1000''s)')
ylabel('Delta, Gamma, and Vega Portfolio Dollar Sensitivities')
title ('Portfolio Sensitivities Profile')
legend('Delta', 'Gamma', 'Vega', 0)

Восстановление баланса затрат

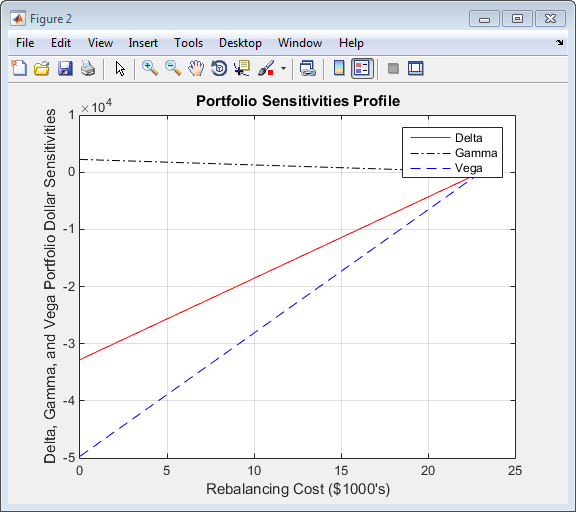
В этой форме вызова, hedgeopt вызовы hedgeslf внутренне определить максимальные затраты, необходимые для минимизации чувствительности портфеля (23 055,90 долл. США), и равномерно определить границы расходов в пределах от 0 до 23 055,90 долл. США.

Оба hedgeopt и hedgeslf приведите задачу оптимизации как ограниченный линейный метод наименьших квадратов задачу. В зависимости от инструментов и ограничений ни одна из функций не гарантировано сходится к решению. В некоторых случаях пространство задач может быть неограниченным, и для сходимости могут потребоваться дополнительные ограничения равенства инструментов или пользовательские ограничения. Дополнительные сведения см. в разделе Хеджирование с ограниченными портфелями.

См. также

hedgeopt | hedgeslf

Документация