hwcalbyfloor
Калибровка дерева Hull-White с использованием полов
Синтаксис
Описание
[ калибрует Alpha,Sigma,OptimOut] = hwcalbyfloor(RateSpec,MarketStrikeMarketMaturity,MarketVolatility)Alpha (средняя реверсия) и Sigma (волатильность) с использованием данных рынка этажей и модели Халла-Уайта с использованием всей поверхности этажа.
Калибровочные функции Халла-Уайта (hwcalbyfloor и hwcalbycap) поддерживают три модели: Black (по умолчанию), Bachelier или Normal и Shitted Black. Для получения дополнительной информации см. дополнительные аргументы для Shift и Model.
[ оценивает Alpha,Sigma,OptimOut = hwcalbyfloor(RateSpec,MarketStrikeMarketMaturity,MarketVolatility,Strike,Settle,Maturity)Alpha (средняя реверсия) и Sigma (волатильность) использование данных рынка этажей и модели Халла-Уайта для оценки этажа с определенной зрелостью/волатильностью с помощью дополнительных необязательных входных параметров для Strike, Settle, и Maturity.
Strike, Settle, и Maturity аргументы заданы для калибровки к определенной точке на поверхности волатильности рынка. Если калибровка опущена, она выполняется по всем рыночным инструментам
Для примера калибровки с использованием модели Халла-Уайта с Strike, Settle, и Maturity входные параметры, см. Калибровка модели корпуса-белого с использованием рыночных данных.
[ добавляет необязательные аргументы пары "имя-значение". Alpha,Sigma,OptimOut] = hwcalbyfloor(___,Name,Value)
Примеры
Калибровка модели корпуса-белого по рыночным данным с использованием всей поверхности волатильности пола
В этом примере показано, как использовать hwcalbyfloor входные параметры для MarketStrike, MarketMaturity, и MarketVolatility калибровка модели HW с использованием всей поверхности летучести пола.
Данные о волатильности минимального рынка, охватывающие две забастовки в течение 12 дат погашения.
Reset = 4;
MarketStrike = [0.0590; 0.0790];
MarketMaturity = {'21-Mar-2008'; '21-Jun-2008'; '21-Sep-2008'; '21-Dec-2008';
'21-Mar-2009'; '21-Jun-2009'; '21-Sep-2009'; '21-Dec-2009';
'21-Mar-2010'; '21-Jun-2010'; '21-Sep-2010'; '21-Dec-2010'};
MarketMaturity = datenum(MarketMaturity);
MarketVolaltility = [0.1533 0.1731 0.1727 0.1752 0.1809 0.1800 0.1805 0.1802...
0.1735 0.1757 0.1755 0.1755;
0.1526 0.1730 0.1726 0.1747 0.1808 0.1792 0.1797 0.1794...
0.1733 0.1751 0.1750 0.1745];
Постройте поверхность волатильности рынка.
[AllMaturities,AllStrikes] = meshgrid(MarketMaturity,MarketStrike); figure; surf(AllMaturities,AllStrikes,MarketVolaltility) datetick xlabel('Maturity') ylabel('Strike') zlabel('Volatility') title('Market Volatility Data')
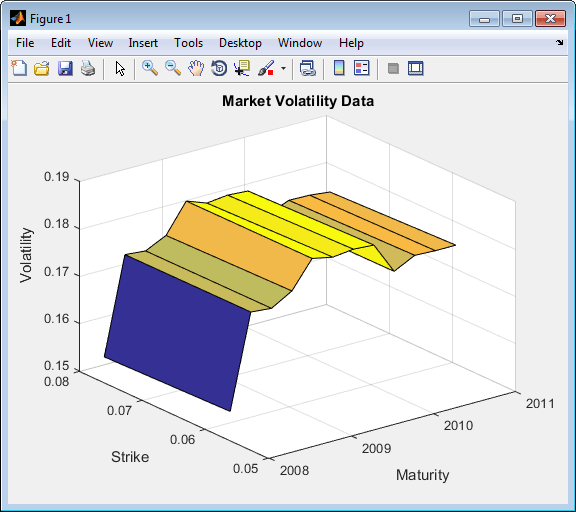
Установите структуру терминов процентной ставки и создайте RateSpec.
Settle = '21-Jan-2008'; Compounding = 4; Basis = 0; Rates= [0.0627; 0.0657; 0.0691; 0.0717; 0.0739; 0.0755; 0.0765; 0.0772; 0.0779; 0.0783; 0.0786; 0.0789]; EndDates = {'21-Mar-2008';'21-Jun-2008';'21-Sep-2008';'21-Dec-2008';... '21-Mar-2009';'21-Jun-2009';'21-Sep-2009';'21-Dec-2009';.... '21-Mar-2010';'21-Jun-2010';'21-Sep-2010';'21-Dec-2010'}; RateSpec = intenvset('ValuationDate', Settle, 'StartDates', Settle,... 'EndDates', EndDates,'Rates', Rates, 'Compounding', Compounding,... 'Basis',Basis)
RateSpec =
FinObj: 'RateSpec'
Compounding: 4
Disc: [12x1 double]
Rates: [12x1 double]
EndTimes: [12x1 double]
StartTimes: [12x1 double]
EndDates: [12x1 double]
StartDates: 733428
ValuationDate: 733428
Basis: 0
EndMonthRule: 1Калибровка модели Халла-Уайта по рыночным данным.
o = optimoptions('lsqnonlin','TolFun',1e-5,'Display','off'); [Alpha, Sigma] = hwcalbyfloor(RateSpec, MarketStrike, MarketMaturity,... MarketVolaltility, 'Reset', Reset,'Basis', Basis, 'OptimOptions', o)
Warning: LSQNONLIN did not converge to an optimal solution. It exited with exitflag = 3.
> In hwcalbycapfloor>optimizeOverCapSurface at 232
In hwcalbycapfloor at 79
In hwcalbyfloor at 81
Alpha =
0.0835
Sigma =
0.0145
Сравните с черными ценами.
BlkPrices = floorbyblk(RateSpec,AllStrikes(:), Settle, AllMaturities(:),... MarketVolaltility(:),'Reset',Reset,'Basis',Basis)
BlkPrices =
0
0.2659
0.0010
0.5426
0.0021
0.6841
0.0042
0.7947
0.0081
0.8970
0.0128
0.9947
0.0217
1.1145
0.0340
1.2448
0.0402
1.3415
0.0610
1.4947
0.0827
1.6458
0.1071
1.7951
Setup дерева Hull-White с использованием калиброванных параметров, альфа и сигмы.
VolDates = EndDates; VolCurve = Sigma*ones(numel(EndDates),1); AlphaDates = EndDates; AlphaCurve = Alpha*ones(numel(EndDates),1); HWVolSpec = hwvolspec(Settle, VolDates, VolCurve, AlphaDates, AlphaCurve); HWTimeSpec = hwtimespec(Settle, EndDates, Compounding); HWTree = hwtree(HWVolSpec, RateSpec, HWTimeSpec, 'Method', 'HW2000')
HWTree =
FinObj: 'HWFwdTree'
VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
tObs: [0 0.6593 1.6612 2.6593 3.6612 4.6593 5.6612 6.6593 7.6612 8.6593 9.6612 10.6593]
dObs: [733428 733488 733580 733672 733763 733853 733945 734037 734128 734218 734310 734402]
CFlowT: {1x12 cell}
Probs: {1x11 cell}
Connect: {1x11 cell}
FwdTree: {1x12 cell}Вычислите цены Hull-White на основе калиброванного дерева.
HWPrices = floorbyhw(HWTree, AllStrikes(:), Settle, AllMaturities(:), Reset, Basis)
HWPrices =
0
0.2644
0.0067
0.5404
0.0101
0.6924
0.0169
0.7974
0.0236
0.8919
0.0320
0.9919
0.0460
1.1074
0.0649
1.2340
0.0829
1.3558
0.1096
1.4957
0.1406
1.6418
0.1724
1.7877Граф Черные цены относительно калиброванных цен на дерево Халл-Уайт.
figure; plot(AllMaturities(:), BlkPrices, 'or', AllMaturities(:), HWPrices, '*b'); datetick('x', 2) xlabel('Maturity'); ylabel('Price'); title('Black and Calibrated (HW) Prices'); legend('Black Price', 'Calibrated HW Tree Price','Location', 'NorthWest'); grid on
Калибровка поплавков с использованием модели Normal (Bachelier)
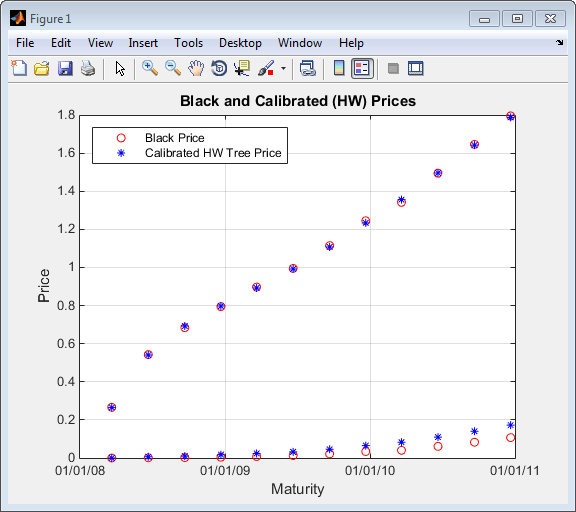
В этом примере показано, как использовать hwcalbyfloor калибровка рыночных данных с помощью модели Normal (Bachelier) для определения цены на флорлеты. Используйте модель Normal (Bachelier), чтобы выполнить калибровку при работе с отрицательными процентными ставками, ударами и нормальными подразумеваемыми волатильностями.
Рассмотрим этаж с этими параметрами:
Settle = 'Dec-30-2016'; Maturity = 'Dec-30-2019'; Strike = -0.004075; Reset = 2; Principal = 100; Basis = 0;
Половицы и рыночные данные для этого примера определяются как:
floorletDates = cfdates(Settle, Maturity, Reset, Basis); datestr(floorletDates')
ans = 6x11 char array
'30-Jun-2017'
'30-Dec-2017'
'30-Jun-2018'
'30-Dec-2018'
'30-Jun-2019'
'30-Dec-2019'
% Market data information MarketStrike = [-0.00595; 0]; MarketMat = {'30-Jun-2017';'30-Dec-2017';'30-Jun-2018'; '30-Dec-2018';'30-Jun-2019'; '30-Dec-2019'}; MarketVol = [0.184 0.2329 0.2398 0.2467 0.2906 0.3348; % First row in table corresponding to Strike 1 0.217 0.2707 0.2760 0.2814 0.3160 0.3508]; % Second row in table corresponding to Strike 2
Определите RateSpec.
Rates= [-0.003210;-0.003020;-0.00182;-0.001343;-0.001075]; ValuationDate = 'Dec-30-2016'; EndDates = {'30-Jun-2017';'Dec-30-2017';'30-Jun-2018';'Dec-30-2018';'Dec-30-2019'}; Compounding = 2; Basis = 0; RateSpec = intenvset('ValuationDate', ValuationDate, ... 'StartDates', ValuationDate, 'EndDates', EndDates, ... 'Rates', Rates, 'Compounding', Compounding, 'Basis', Basis);
Использование hwcalbyfloor чтобы найти значения параметров волатильности Alpha и Sigma использование модели Normal (Bachelier).
format short o=optimoptions('lsqnonlin','TolFun',100*eps); warning ('off','fininst:hwcalbycapfloor:NoConverge') [Alpha, Sigma, OptimOut] = hwcalbyfloor(RateSpec, MarketStrike, MarketMat,... MarketVol, Strike, Settle, Maturity, 'Reset', Reset, 'Principal', Principal,... 'Basis', Basis, 'OptimOptions', o, 'model', 'normal')
Local minimum possible. lsqnonlin stopped because the size of the current step is less than the value of the step size tolerance.
Alpha = 1.0000e-06
Sigma = 0.3410
OptimOut = struct with fields:
resnorm: 1.9233e-04
residual: [5x1 double]
exitflag: 2
output: [1x1 struct]
lambda: [1x1 struct]
jacobian: [5x2 double]
The OptimOut.residual поле OptimOut структура является невязкой оптимизации. Это значение содержит различие между настилами Normal (Bachelier) и этажами, рассчитанными во время оптимизации. Используйте OptimOut.residual значение, чтобы вычислить процентное различие (ошибку) по сравнению с нормальными ценами (Bachelier) на полу, а затем решить, является ли невязка приемлемым. Есть почти всегда какой-то остаточный, поэтому решите, приемлемо ли параметризовать рынок с одним значением Alpha и Sigma.
Оцените полы с помощью рыночных данных и модели Normal (Bachelier), чтобы получить эталонные значения полов. Чтобы определить эффективность оптимизации, вычислите эталонные значения полов с помощью формулы Normal (Bachelier) и рыночных данных. Обратите внимание, что сначала необходимо интерполировать рыночные данные, чтобы получить флорлеты для вычисления.
MarketMatNum = datenum(MarketMat); [Mats, Strikes] = meshgrid(MarketMatNum, MarketStrike); FlatVol = interp2(Mats, Strikes, MarketVol, datenum(Maturity), Strike, 'spline'); [FloorPrice, Floorlets] = floorbynormal(RateSpec, Strike, Settle, Maturity, FlatVol,... 'Reset', Reset, 'Basis', Basis, 'Principal', Principal); Floorlets = Floorlets(2:end)'
Floorlets = 5×1
4.7637
6.7180
8.1833
9.5825
10.6090
Сравните оптимизированные значения и значения Normal (Bachelier) и отобразите результаты графически. После вычисления ссылочных значений для floorlets сравните значения аналитически и графически, чтобы определить, рассчитаны ли отдельные значения Alpha и Sigma обеспечивают адекватное приближение.
OptimFloorlets = Floorlets+OptimOut.residual;
disp(' ');disp(' Bachelier Calibrated Floorlets');Bachelier Calibrated Floorlets
disp([Floorlets OptimFloorlets])
4.7637 4.7685
6.7180 6.7263
8.1833 8.1878
9.5825 9.5795
10.6090 10.6007
plot(MarketMatNum(2:end), Floorlets, 'or', MarketMatNum(2:end), OptimFloorlets, '*b'); datetick('x', 2) xlabel('Floorlet Maturity'); ylabel('Floorlet Price'); ylim ([0 16]); title('Bachelier and Calibrated Floorlets'); h = legend('Bachelier Floorlets', 'Calibrated Floorlets'); set(h, 'color', [0.9 0.9 0.9]); set(h, 'Location', 'SouthEast'); set(gcf, 'NumberTitle', 'off') grid on
Входные параметры
Выходные аргументы
См. также
floorbyblk | HullWhite1F | hwcalbycap | hwtree | lsqnonlin