Exponenta Banner

ncfsyn

Проект формирования цикла с использованием метода Гловера-Макфарлейна

Свернуть все на странице

Синтаксис

[K,CL,gamma,info] = ncfsyn(G)
[K,CL,gamma,info] = ncfsyn(G,W1)
[K,CL,gamma,info] = ncfsyn(G,W1,W2)

Описание

ncfsyn реализует способ разработки контроллеров, который использует комбинацию формирования цикла и устойчивой стабилизации, как предложено в [1][2]-. Функция вычисляет нормализованный coprime контроллер формирования цикла фактора перчаточника-McFarlane <reservedrangesplaceholder4>  K для объекта G с весами <reservedrangesplaceholder1> 1 предварительного компенсатора и посткомпенсатора и <reservedrangesplaceholder0> 2. Функция принимает положительную обратную связь строения из следующего рисунка.

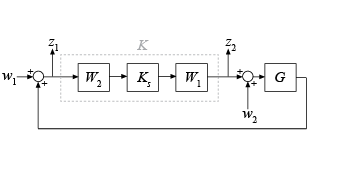
Чтобы задать отрицательную обратную связь, замените G на - G. Контроллер Ks стабилизирует семейство систем, заданное шаром неопределенности в нормализованных простых факторах формируемого объекта Gs = W 2 G W 1. Конечный контроллер K возвращенncfsyn получается как K = W 1 Ks W 2.

[K,CL,gamma,info] = ncfsyn(G) вычисляет H Гловера-Макфарлейна ∞ нормализованного контроллера формирования контура общего фактора K для объекта G, с W 1 = W 2 = I. CL - система с обратной связью от возмущений w 1 и w 2 до выходов z 1 и z 2. Функция также возвращает H ∞ эффективность gammaи структуру, содержащую дополнительную информацию о результате.

пример

[K,CL,gamma,info] = ncfsyn(G,W1) вычисляет контроллер с помощью веса предкомпенсатора, заданного в W1, с W 2 = I.

[K,CL,gamma,info] = ncfsyn(G,W1,W2) вычисляет контроллер с помощью заданного веса предкомпенсатора W1 и вес посткомпенсатора W2.

Примеры

свернуть все

Открыть Live Script

Использование ncfsyn для разработки контроллера для следующего объекта. 

G = tf([1 5],[1 2 10]);

Используйте функции взвешивания, которые приводят к формованному объекту W1*G*W2 с высоким усилением для нарушения порядка ниже 0,1 рад/с и низким усилением для хорошей устойчивой устойчивости выше около 5 рад/с. Для этого Gдостаточен только вес предкомпенсатора. 

W1 = tf(1,[1 0]);
bodemag(W1*G)
grid

Figure contains an axes. The axes contains an object of type line. This object represents untitled1.

Вычислите контроллер.

[K,CL,gamma,info] = ncfsyn(G,W1);

Оптимальная стоимость gamma связана с нормализованным запасом устойчивости системы по 1/gamma = ncfmargin(Gs,-Ks). (Знак минус нужен, потому что ncfmargin принимает цикл отрицательной обратной связи, в то время как ncfsyn вычисляет контроллер положительной обратной связи.) 

b = ncfmargin(info.Gs,-info.Ks);
[gamma 1/b]
ans = 1×2

    1.4508    1.4508

Сравните достигнутые и целевые формы цикла. 

sigma(G*K,G*W1)
legend('achieved','target')

Figure contains an axes. The axes contains 2 objects of type line. These objects represent achieved, target.

Входные параметры

свернуть все

Объект, заданный как динамическая системная модель, такая как пространство состояний (ss) модель. Если G является обобщенной моделью пространства состояний с неопределенными или настраиваемыми блоками системы управления, затем ncfsyn использует номинальное или текущее значение этих элементов. G должно иметь одинаковое количество входов и выходов.

Вес предкомпенсатора, указанный как:

  • Единичные матричные eye(N), где N количество входов или выходов в G.

  • SISO минимально-фазовая модель LTI. В этом случае, ncfsyn использует тот же вес для каждого контурного канала.

  • Минимально-фазовая модель LTI MIMO тех же размерностей ввода-вывода, что и G.

Выберите веса предкомпенсатора и посткомпенсатора W 1 и W 2 таким образом, чтобы коэффициент усиления сформированного объекта Gs = W 2 G W 1 был достаточно высоким на частотах, где требуется хорошее ослабление возмущения, и достаточно низким на частотах, где требуется хорошая устойчивость.

Вес посткомпенсатора, заданный как матрица тождеств eye(N) или модель SISO или MIMO LTI. Факторы для определения W2 те же, что и для W1.

Выходные аргументы

свернуть все

H ∞ -оптимальный контроллер формирования цикла, возвращенный как пространство состояний (ss) модель с такими же вводами-выводами размерностей как G. Оптимальный контроллер K = W 1 Ks W 2. См. Алгоритмы.

Оптимальная система с обратной связью от возмущений w 1 и w 2 до выходов z 1 и z 2, возвращенная как модель пространства состояний. Система с обратной связью определяется:

[IK](I−GK)−1[I, G].

H производительность ∞, достигнутая с помощью контроллера K, возвращенное как положительная скалярная величина значение, больше 1. Производительность H ∞ hinfnorm(CL). Оптимальный контроллер Ks таков, что график сингулярного значения имеющего форму цикла Ls = <reservedrangesplaceholder5> 2 <reservedrangesplaceholder4> <reservedrangesplaceholder3> 1 <reservedrangesplaceholder2> оптимально соответствует целевой форме цикла Gs к в факторе gamma. Однако по численным причинам, ncfsyn обычно возвращает контроллер с немного большей H ∞ эффективностью, чем оптимальная. Для оптимальной достижимой производительности смотрите info выходной аргумент.

gamma связана с нормализованным запасом устойчивости системы по gamma = 1/ncfmargin(Gs,-Ks). Таким образом, gamma дает хорошее показание робастности устойчивости широкому классу неструктурированных изменений объекта со значениями в области значений 1 < gamma < 3 соответствует удовлетворительным запасам устойчивости для большинства типичных разработок системы управления.

Дополнительная информация о синтезе контроллера, возвращенная как структура, содержащая следующие поля.

  • gopt - Оптимальная эффективность, достигаемая путем H ∞ синтеза для формованного объекта. По числовым причинам ,ncfsyn обычно возвращает контроллер с несколько большей H ∞ эффективностью, которая возвращается в gamma.

  • emax — nugap метрика робастности, emax = 1/gopt (см. gapmetric)

  • Gs - Фасонное растение Gs = W 2 G W 1

  • Ks - Оптимальный контроллер для фасонных Gs. Конечный контроллер - K = W 1 Ks W 2. Смотрите Алгоритмы для получения дополнительной информации.

Совет

  • В то время как ncfmargin принимает цикл отрицательной обратной связи, ncfsyn команда проектирует контроллер для цикла положительной обратной связи. Поэтому вычислить запас можно с помощью контроллера, разработанного с ncfsyn, использовать [marg,freq] = ncfmargin(G,K,+1).

Алгоритмы

Возвращенный контроллер K = <reservedrangesplaceholder5> 1 <reservedrangesplaceholder4> <reservedrangesplaceholder3> 2, где Ks оптимальный контроллер <reservedrangesplaceholder1> , который минимизирует стоимость <reservedrangesplaceholder0> 

γ(Ks)=‖[IKs](I−GsKs)−1[I,Gs]‖∞=‖[IGs](I−KsGs)−1[I,Ks]‖∞.

Оптимальная эффективность - это минимальная стоимость

γ:=minKsγ(Ks).

Предположим, что Gs = NM–1, где N (<reservedrangesplaceholder8>) * N (<reservedrangesplaceholder6>) + M (<reservedrangesplaceholder4>) * M (<reservedrangesplaceholder2>) = I, нормализованная coprime факторизация (NCF) взвешенной модели объекта управления Gs. Затем теория гарантирует, что система управления остается устойчивой для любого возмущенияG˜s к Gs формы

G˜s=(N+Δ1)(M+Δ2)−1

где Δ1, Δ2 являются стабильной парой, удовлетворяющей

‖[Δ1Δ2]‖∞<MARG:=1γ.

Цель H ∞ -norm с обратной связью имеет стандартную интерпретацию усиления сигнала. Наконец, можно показать, что контроллер, Ks, существенно не влияет на форму контура в частотах, где коэффициент усиления W 2 GW 1 является либо высоким, либо низким, и гарантирует удовлетворительные пределы устойчивости в частотной области пересечения коэффициента усиления. В настройке регулятора конечный контроллер, который будет реализован, является K = W 1 Ks W 2.

Для получения дополнительной информации см. McFarlane and Glover [1] - [2].

Вопросы совместимости

расширить все

Не рекомендуемый запуск в R2020b

Ссылки

[1] McFarlane, D.C., and K. Glover, Robust Controller Design using Normalized Coprime Factor Plant Descriptions, Springer Verlag, Lecture Notes in Control and Information Sciences, voes, vol. 138, 1989.

[2] McFarlane, D.C., and K. Glover, «A Loop Shaping Design Procedure Using Synthesis», Транзакции IEEE по автоматическому управлению, том 37, № 6, стр. 759 - 769, июнь 1992.

[3] Винникомб, Г., «Измерение робастности систем обратной связи», докторская диссертация, инженерный факультет, Кембриджский университет, 1993.

[4] Zhou, K., and J.C. Doyle, Essentials of Robust Control. Нью-Йорк: Prentice Hall, 1998.

См. также

| | | |

Темы

Представлено до R2006a

Документация по Robust Control Toolbox

Поддержка