Первичная цель образцового выбора выбирает самую экономную модель, которая соответственно соответствует вашим данным. Три асимптотически эквивалентных теста сравнивают ограниченную модель (пустая модель) против неограниченной модели (альтернативная модель), подгонка к тем же данным:
Тест отношения правдоподобия (LR)
Тест множителя Лагранжа (LM)
Вальд (W) тест
Для модели с параметрами θ рассмотрите ограничение который удовлетворен пустой моделью. Например, рассмотрите тестирование нулевой гипотезы Функция ограничения для этого теста
LR, LM и Вальдовы тесты приближаются к проблеме сравнения припадка ограниченной модели против неограниченной модели по-другому. Для набора определенных данных позволить обозначьте функцию loglikelihood, выполненную в оценке наибольшего правдоподобия (MLE) ограниченной (пустой) модели. Пусть обозначьте функцию loglikelihood, выполненную в MLE неограниченной (альтернативной) модели. Следующая фигура иллюстрирует объяснение позади каждого теста.
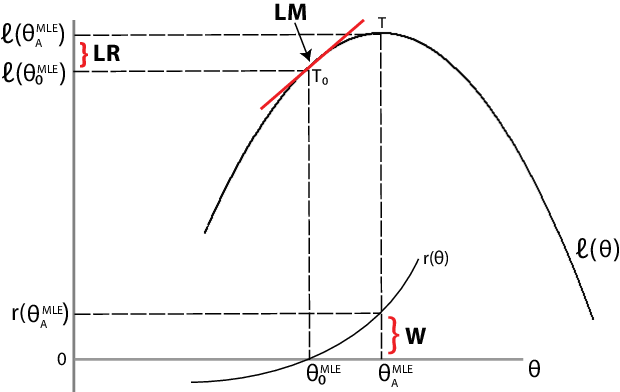
Тест отношения правдоподобия. Если ограниченная модель соответствует, то различие между максимизируемыми целевыми функциями, не должен значительно отличаться от нуля.
Тест множителя Лагранжа. Если ограниченная модель соответствует, то наклон касательной функции loglikelihood в ограниченном MLE (обозначенный T0 в фигуре) не должен значительно отличаться от нуля (который является наклоном касательной функции loglikelihood в неограниченном MLE, обозначенном T).
Вальдов тест. Если ограниченная модель соответствует, то функция ограничения, выполненная в неограниченном MLE, не должна значительно отличаться от нуля (который является значением функции ограничения в ограниченном MLE).
Три теста асимптотически эквивалентны. Под пустым указателем LR, LM и Вальдова тестовая статистика все распределяются как со степенями свободы равняются количеству ограничений. Если тестовая статистическая величина превышает тестовое критическое значение (эквивалентно, p-значение меньше чем или равно уровню значения), нулевая гипотеза отклоняется. Таким образом, ограниченная модель отклоняется в пользу неограниченной модели.
Выбирание среди LR, LM и Вальдового теста в основном определяется вычислительной стоимостью:
Чтобы провести тест отношения правдоподобия, необходимо оценить и ограниченные и неограниченные модели.
Чтобы провести тест множителя Лагранжа, только необходимо оценить ограниченную модель (но тест требует оценки ковариационной матрицы отклонения).
Чтобы провести Вальдов тест, только необходимо оценить неограниченную модель (но тест требует оценки ковариационной матрицы отклонения).
При прочих равных условиях тест LR часто является предпочтительным вариантом для сравнения вложенных моделей. Econometrics Toolbox™ имеет функциональность для всех трех тестов.
Можно провести тест отношения правдоподобия с помощью lratiotest. Необходимые входные параметры:
Значение максимизируемого неограниченного loglikelihood,
Значение максимизируемого ограничило loglikelihood,
Количество ограничений (степени свободы)
Учитывая эти входные параметры, тестовая статистическая величина отношения правдоподобия
При оценке условного среднего значения и моделей отклонения (использующий arima, garch, egarch или gjr), можно возвратить значение loglikelihood целевой функции как дополнительный выходной аргумент estimate или infer. Для многомерных моделей временных рядов можно получить значение loglikelihood целевой функции с помощью estimate.
Необходимые входные параметры для проведения теста множителя Лагранжа:
Градиент неограниченной вероятности оценен в ограниченном MLEs (счет), S
Ковариационная матрица отклонения для неограниченных параметров, оцененных в ограниченном MLEs, V
Учитывая эти входные параметры, тестовая статистическая величина LM
Можно провести тест LM с помощью lmtest. Определенным примером теста LM является тест ДУГИ Энгла, который можно провести использование archtest.
Необходимые входные параметры для проведения Вальдового теста:
Функция ограничения выполнена в неограниченном MLE, r
Якобиан функции ограничения оценен в неограниченном MLEs, R
Ковариационная матрица отклонения для неограниченных параметров, оцененных в неограниченном MLEs, V
Учитывая эти входные параметры, тестовая статистическая величина для Вальдового теста
Можно провести Вальдов тест с помощью waldtest.
Можно часто вычислять якобиан функции ограничения аналитически. Или, если у вас есть Symbolic Math Toolbox™, можно использовать функциональный jacobian.
Для оценки ковариационной матрицы отклонения существует несколько общепринятых методик, включая:
Векторное произведение градиентов (OPG). Позвольте G быть матрицей градиентов функции loglikelihood. Если ваш набор данных имеет наблюдения N, и в неограниченной вероятности существуют параметры m, то G является N × матрица m.
Матрица оценка OPG ковариационной матрицы отклонения.
Для arima, garch, egarch и моделей gjr, метод estimate возвращает оценку OPG ковариационной матрицы отклонения.
Обратный отрицательный гессиан (INH). Учитывая функцию loglikelihood оценка ковариации INH имеет элементы
Функция оценки для многомерных моделей, estimate, возвращает ожидаемую ковариационную матрицу отклонения Гессиана.
Если у вас есть Symbolic Math Toolbox, можно использовать jacobian дважды, чтобы вычислить матрицу Гессиана для функции loglikelihood.
lmtest | lratiotest | waldtest