Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Мы представляем набор изображений, иллюстрирующих возможности существующей графической системы MuPAD®. Эти изображения создаются в различных местах в этом документе, где они используются, чтобы продемонстрировать определенные функции графической системы. Ссылка на местоположение подробной документации обеспечивается наряду с каждым изображением в этой галерее. Там, более подробная информация включая команды MuPAD для генерации изображения может быть найдена.
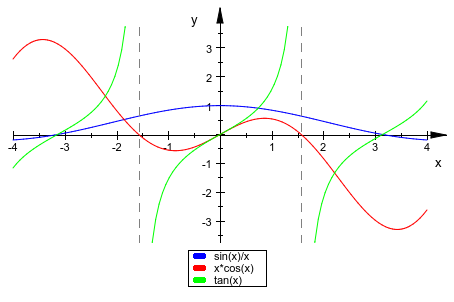
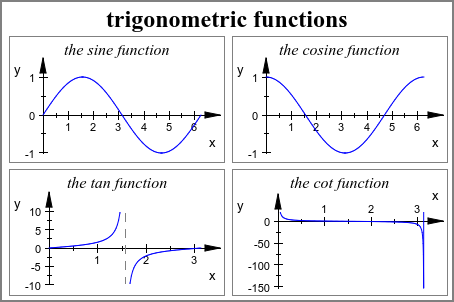
Следующее изображение показывает график нескольких функций. Особенности подсвечены “вертикальными асимптотами”. См. 2D Функциональные Графики: plotfunc2d для деталей:
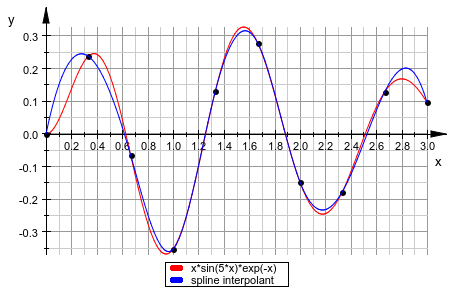
Следующее изображение показывает график функций вместе с интерполяцией сплайна через набор точек выборки. Смотрите раздел Some Examples для деталей:
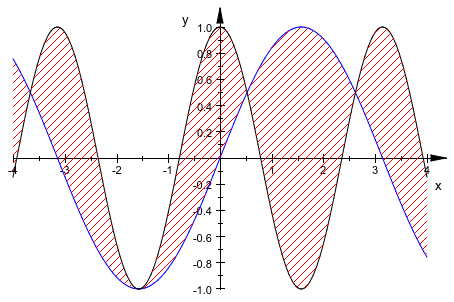
Следующее изображение показывает заштрихованную область между функциями. Смотрите примеры на странице справки plot::Hatch для деталей:
Следующее изображение демонстрирует некоторые возможности размещения. Смотрите примеры на странице справки Layout для деталей:
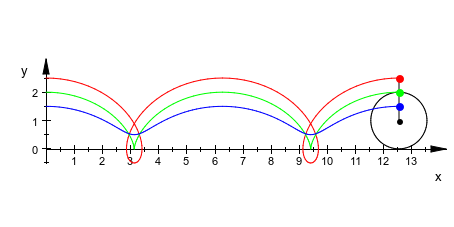
Следующее изображение демонстрирует конструкцию циклоид через точки, зафиксированные к прокручивающемуся колесу. Смотрите раздел Some Examples для анимированной версии и деталей:
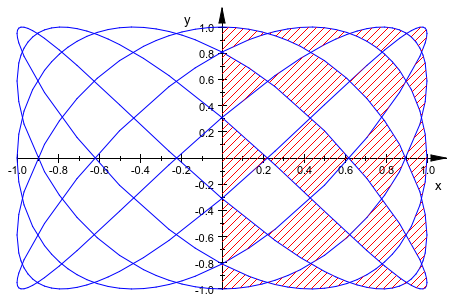
Следующее изображение демонстрирует заштрихованные области в кривых. Смотрите примеры на странице справки plot::Hatch для деталей:
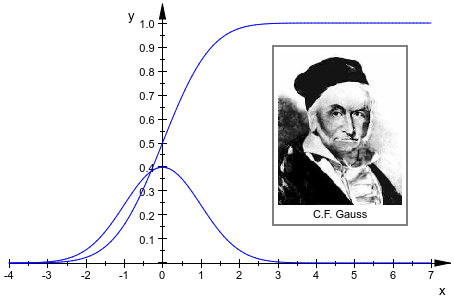
Следующее изображение показывает импортированное растровое изображение в графиках функций. Смотрите раздел Importing Pictures для деталей:
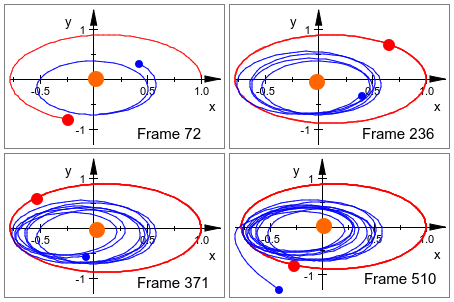
Следующее изображение показывает некоторые кадры анимации встревоженной орбиты небольшой планеты, вышибленной из солнечной системы гигантской планетой после почти столкновения. Смотрите раздел Example 3 для деталей анимации:
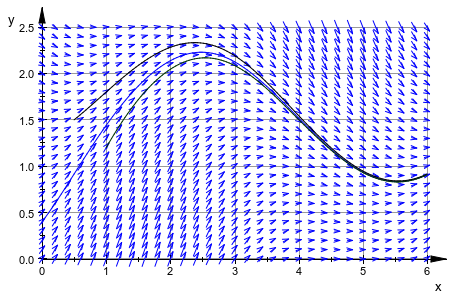
Следующее изображение показывает три кривые решения ОДУ в направленном векторном поле, сопоставленном с ОДУ. Смотрите примеры на странице справки plot::VectorField2d для деталей:
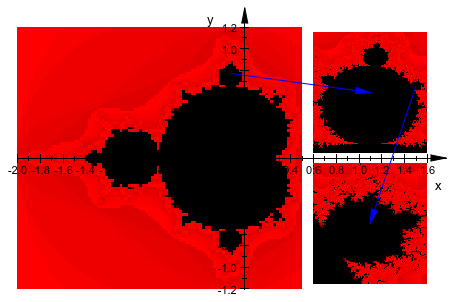
Следующее изображение показывает Множество Мандельброта вместе с двумя взлетами удара особенно интересных областей. Смотрите примеры на странице справки plot::Density для деталей:
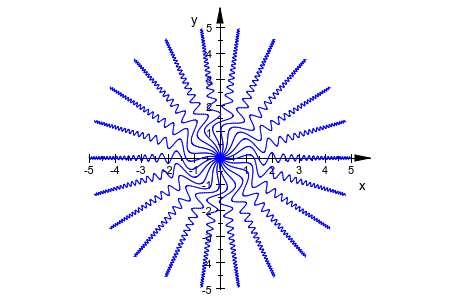
Следующее изображение показывает несколько вращаемых копий функционального графика. Смотрите примеры на странице справки plot::Rotate2d для деталей:
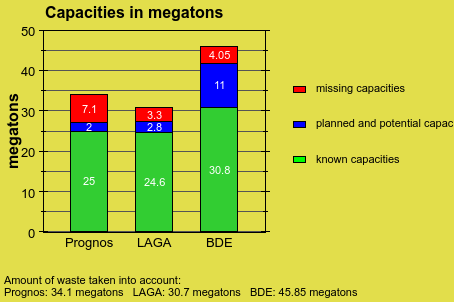
Следующее изображение показывает график данных типа plot::Bars2d. Смотрите примеры на странице справки plot::Bars2d для деталей:
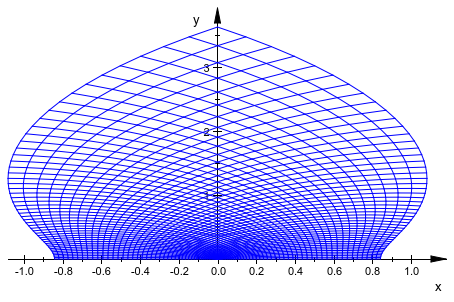
Следующее изображение показывает изображение прямоугольника в комплексной плоскости в соответствии с картой
. Смотрите примеры на странице справки plot::Conformal для деталей:
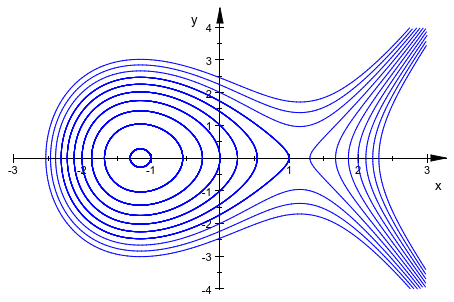
Следующее изображение показывает некоторые эллиптические кривые, сгенерированные как контурный график. Смотрите примеры на странице справки plot::Implicit2d для деталей:
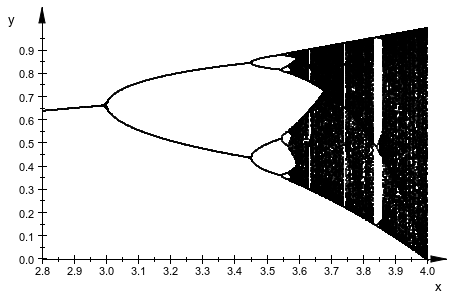
Следующее изображение показывает схему Feigenbaum логистической карты. Смотрите примеры на странице справки plot::PointList2d для деталей:
Следующее изображение показывает фрактальный объект, сгенерированный графиком черепахи системы Lindenmayer. Смотрите примеры на странице справки plot::Lsys для деталей:
Следующее изображение демонстрирует 3D график функций
, где
Bessel function of the first kind. Смотрите примеры на странице справки plot::Function3d для деталей:
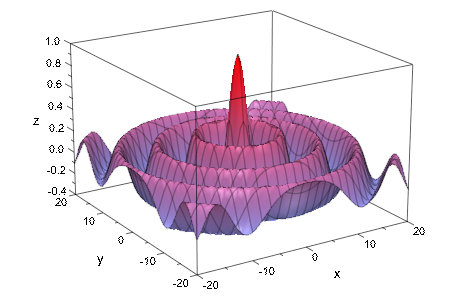
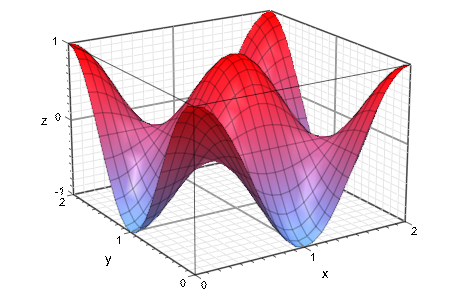
Следующее изображение демонстрирует 3D график функций, улучшенный координатной сеткой. Смотрите примеры на странице справки GridVisible для деталей:
Следующее изображение демонстрирует 3D график функций
, который не действителен для некоторых частей пространства параметров. См. документацию plot::Function3d для деталей:
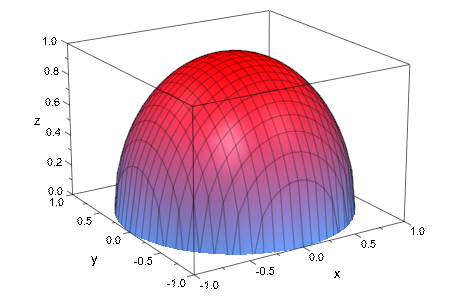
Следующее изображение показывает “бутылку Клейна” (известный топологический объект). Эта поверхность не имеет ориентации; нет никакой “внутренней части” и никакой “внешней стороны” этого объекта. Смотрите примеры на странице справки plot::Surface для деталей:
Следующее изображение демонстрирует реконструкцию объекта с осевой симметрией от измерений его радиуса в различных точках. Смотрите раздел Some Examples для деталей:
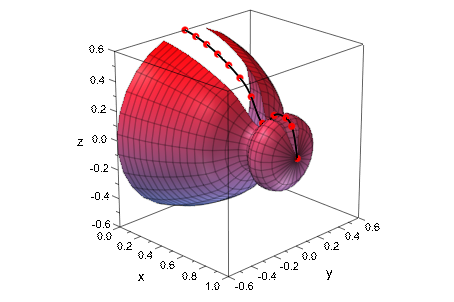
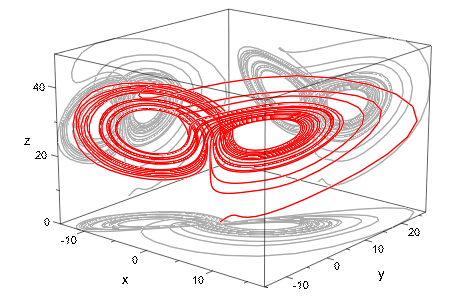
Следующее изображение показывает “Аттрактор Лоренца”. Смотрите раздел Cameras в 3D для анимированной версии и деталей:
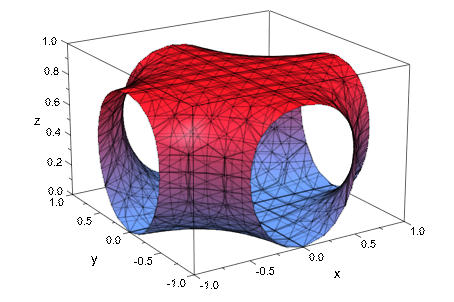
Следующее изображение показывает 3D поверхность уровня функции (набор решения z 2 = sin (z - x 2 y2)). Смотрите примеры на странице справки plot::Implicit3d для деталей:
