linalg::invvandermondeМатрицы Вандермонда и их инверсии
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::invvandermonde([v1, v2, …], <R>)
linalg::invvandermonde(v1, v2, ... , vn) возвращает инверсию матрицы Вандермонда с узлами v i.
Используйте linalg::invvandermonde([v1, ..., vn], R) задавать n ×n обратная матрица Вандермонда по полю R. Обратите внимание на то, что узлы v i должны быть элементами R или должно быть конвертируемым к элементам R.
Матрицы Вандермонда размерности n ×n могут быть инвертированы с операциями O (n 2). Линейные уравнения с матрицей коэффициентов Вандермонда могут быть решены через linalg::vandermondeSolve.
Создайте 3×3 матрица Вандермонда:
V := linalg::vandermonde([v1, v2, v3])
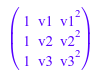
Инверсия этой матрицы:
invV := linalg::invvandermonde([v1, v2, v3])

V и его инверсия является матрицами доменного Dom::Matrix().
domtype(V), domtype(invV)
![]()
Можно задать специальный звонок компонента для матриц, если узлы могут быть преобразованы в элементы звонка. Например, спецификация доменного Dom::Float генерирует записи с плавающей точкой:
V := linalg::vandermonde([2, PI, 1/3], Dom::Float)

domtype(V)
![]()
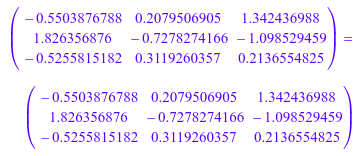
Это быстрее, чтобы вычислить инверсию через linalg::invvandermonde чем инвертирование матрицы Вандермонда типовым алгоритмом инверсии, реализованным V^(-1):
V^(-1) = linalg::invvandermonde([2, PI, 1/3], Dom::Float)
delete V, invV
|
Узлы Вандермонда: арифметические выражения |
|
Звонок компонента: область категории |
n ×n матрица доменного Dom::Matrix(R).
Матрицы Вандермонда известно плохо обусловлены. Инверсии больших матриц Вандермонда с плавающей точкой подвергаются серьезным эффектам округления.