linalg::toeplitzSolveРешите линейную систему Теплица
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::toeplitzSolve(t, y)
linalg::toeplitzSolve(t, y) возвращает решение
линейной системы Теплица
с i = 1, …, n.
linalg::toeplitzSolve(t, y) с t = [t k, …, t 0, …, t - k] и y = [y 1, …, y n] решает n ×n система Теплица
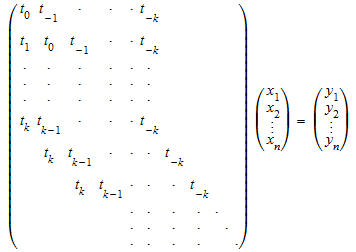
с полосами 2 k + 1.
linalg::toeplitzSolve реализует алгоритм Левинсона. Это использует O (n 2) элементарные операции, чтобы решить систему Теплица. Требованиями к памяти является O (n). Для плотных систем Теплица это быстрее, чем общий решатель solve и линейные решатели linsolve, numeric::linsolve, linalg::matlinsolve и numeric::matlinsolve.
Обратите внимание на то, что алгоритм Левинсона требует что все основные несовершеннолетние
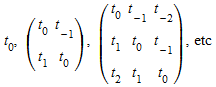
несингулярны.
Если linalg::toeplitzSolve не умеет найти решение из-за этого ограничения, или если система очень разреженна с k, меньшим, чем
, мы рекомендуем сгенерировать соответствующую матрицу Теплица через linalg::toeplitz и вычислите решение через linalg::matlinsolve или numeric::matlinsolve, соответственно. См. Пример 2
linalg::toeplitzSolve может решить системы Теплица по произвольным содействующим звонкам. Только убедитесь, что оба записи Теплица t, а также компоненты 'правой стороны' y являются элементами желаемого содействующего звонка. См. Пример 3.
Записи Теплица t и правая сторона y линейной системы вводятся как векторы-строки:
t := matrix([4, 2, 1, 3, 5]): y := matrix([y1, y2, y3]):
Решение системы Теплица возвращено как вектор того же типа как входной вектор y:
x := linalg::toeplitzSolve(t, y): x, domtype(x)
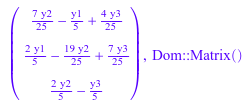
Если входной вектор является списком, выход является списком, также:
x := linalg::toeplitzSolve(t, [y1, y2, y3]): x, domtype(x)
delete t, y, x:
Алгоритм Левинсона не может решить следующую систему Теплица, потому что первый основной несовершеннолетний матрицы Теплица (центральный элемент записей Теплица) исчезает:
linalg::toeplitzSolve([1, 0, 1], [y1, y2, y3, y4])
Это не обязательно подразумевает, что система Теплица не разрешима. Мы генерируем соответствующую матрицу Теплица и используем типовой линейный решатель, такой как linalg::matlinsolve:
T := linalg::toeplitz(4, 4, [1, 0, 1])
linalg::matlinsolve(T, matrix([y1, y2, y3, y4]))
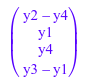
Мы решаем систему Теплица по полю ℤ 7 (целые числа по модулю 7) представленный доменным Dom::IntegerMod(7):
R := Dom::IntegerMod(7): t := [R(5), R(3), R(2), R(5), R(1)]: y := [R(1), R(2), R(3)]: linalg::toeplitzSolve(t, y)
delete R, t, y:
|
Вектор или список с 2 k + 1 элемент. (Вектор (2 k + 1) ×1 или 1 × (2 k + 1) матрица категории |
|
Вектор или список с элементами n |
Вектор или список с элементами n того же доменного типа как элементы y. FAIL возвращен, если алгоритм не преуспевает в том, чтобы найти решение.