partfracРазложение элементарной дроби
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
partfrac(f, <x>) partfrac(f,x,options)
partfrac(f, x) возвращает разложение элементарной дроби рационального выражения f относительно переменной x.
Считайте рациональное выражение![]() полиномами g, p, q, таким что
полиномами g, p, q, таким что degree (p) < degree(q).
Фактор знаменателя в непостоянные и попарные взаимно-простые полиномы q i с целочисленными экспонентами e i:
![]()
Разложение элементарной дроби на основе этой факторизации является представлением
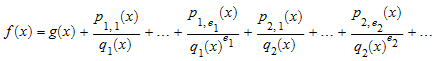
где p i, j является полиномами, такими что degree(pi,j) < degree(qi). В частности, p i, j является константами, если q i является линейным полиномом.
partfrac факторы использования q i найдены factor функция. Эта функция находит факторизацию по полю подразумеваемой коэффициентами знаменателя. Смотрите Пример 2.
Если f имеет только один неопределенный, и вы не используете опции, затем можно не использовать второй аргумент x в вызове partfrac. В противном случае задайте неопределенное как второй параметр.
partfrac может также найти разложение элементарной дроби относительно выражений вместо переменных. Смотрите Пример 3.
Опция Full вызывает полную факторизацию знаменателя в линейные факторы. MaxDegree опция определяет, является ли разложением элементарной дроби символьный sum из RootOf условия или выражение в радикалах. В общем случае корней, принадлежащих неприводимому фактору знаменателя степени пять или больше, нельзя выразить в терминах радикалов. Смотрите Пример 6.
Найдите разложение элементарной дроби следующих выражений. Можно не использовать определение переменной, потому что эти рациональные выражения являются одномерными.
partfrac(x^2/(x^3 - 3*x + 2))
![]()
partfrac(23 + (x^4 + x^3)/(x^3 - 3*x + 2))
![]()
partfrac(x^3/(x^2 + 3*I*x - 2))
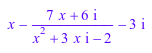
Найдите разложение элементарной дроби следующего выражения, содержащего две переменные, x и y. Для многомерных выражений задайте переменную, относительно которой вы вычисляете разложение элементарной дроби.
f := x^2/(x^2 - y^2): partfrac(f, x), partfrac(f, y)
![]()
delete f:
Найдите разложение элементарной дроби этого выражения.
partfrac(1/(x^2 - 2), x)
![]()
Знаменатель x 2 - 2 не учитывает по рациональным числам.
factor(x^2 - 2)
![]()
Расширьте содействующее поле, используемое factor и partfrac при помощи Adjoin опция.
partfrac(1/(x^2 - 2), x, Adjoin = [sqrt(2)])
![]()
Найдите разложение элементарной дроби относительно выражения, такого как sin(x).
partfrac(1/(sin(x)^4 - sin(x)^2 + sin(x) - 1), sin(x))
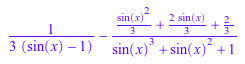
Возвратите список, состоящий из числителей и знаменатели разложения элементарной дроби при помощи List опция.
partfrac(x^2/(x^3 - 3*x + 2), x, List)
![]()
Найдите разложение элементарной дроби с помощью числовой факторизации по полевым вещественным числам, R_.
partfrac(1/(x^3 - 2), x, Domain = R_)
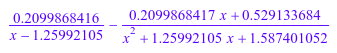
Найдите разложение элементарной дроби того же выражения с помощью числовой факторизации по полевым комплексным числам, C_.
partfrac(1/(x^3 - 2), x, Domain = C_)
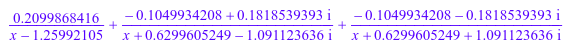
Найдите разложение элементарной дроби, включающее знаменатель в линейные факторы символически. Для этого используйте Full опция.
partfrac(1/(x^3 + x - 2), x, Full)
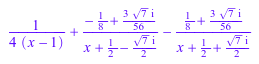
Для неприводимых знаменателей третьих и более высоких степеней разложение элементарной дроби является символьной суммой корней.
S:= partfrac(1/(x^3 + x - 3), x, Full)
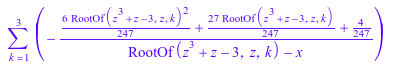
MuPAD® использует freeze функционируйте, чтобы сохранить результат в форме неоцененной символьной суммы. Чтобы оценить эту символьную сумму, используйте unfreeze. Оценка этой символьной суммы упрощает его назад до исходного входа.
unfreeze(S); delete S:
![]()
| |
|
Неопределенный: обычно, идентификатор или индексируемый идентификатор |
|
Включите знаменатель полностью в линейные факторы и найдите разложение элементарной дроби относительно той факторизации. |
|
Возвратите список, состоящий из числителей и знаменатели разложения элементарной дроби. |
|
Опция, заданная как Примкните только к коэффициентам знаменателя с алгебраической степенью, не превышающей |
|
Опция, заданная как Учтите знаменатель по самому маленькому полю, содержащему рациональные числа, все коэффициенты знаменателя и элементы |
|
Опция, заданная как Учтите знаменатель по доменному |
|
Опция, заданная как При создании получившегося выражения вставьте |
f