Типы контроллеров PID для настройки

Система управления настраивающие инструменты PID Toolbox™ может настроить многих PID и диспетчер PID с 2 финансовыми департаментами типы. Термин тип контроллера обозначает, какие термины присутствуют в действии контроллера. Например, PI-контроллер имеет только пропорциональный и интегральный член, в то время как PIDF-контроллер содержит пропорциональные, интеграторные и отфильтрованные производные члены. В этом разделе кратко описываются типы контроллеров PID, доступных для настройки, в следующих инструментах:

Приложение тюнера PID
Настройка задачи контроллера PID в интерактивном редакторе
pidtune команда

Указание типа PID-контроллера

Инструменты настройки PID позволяют проектировать различные типы контроллеров. Способ указания типа контроллера зависит от используемого инструмента.

Настройка командной строки

Для настройки командной строки укажите type аргумент для pidtune команда. Например, C = pidtune(G,'PI') настраивает PI-контроллер для установки G.

Кроме того, если в качестве входного аргумента указан существующий объект контроллера C0, pidtune настраивает новый контроллер того же типа и формы. Например, предположим C0 является pid объект контроллера, имеющий только пропорциональное и производное действие (контроллер PD). Затем, pidtune(G,C0) создает новый pid объект контроллера, который также имеет только пропорциональное и производное действие. Посмотрите pidtune.

Дополнительные сведения о конкретных типах контроллеров, доступных при настройке командной строки, см. в разделе:

Приложение тюнера PID

В приложении PID Tuner можно указать тип контроллера при открытии приложения или изменении типа контроллера в приложении.

Укажите тип при открытии приложения - укажите type аргумент для pidTuner при открытии тюнера PID. Например, pidTuner(G,'PIDF2') открывает PID-тюнер с начальной конструкцией, который является 2-DOF PID-контроллером с фильтром по термину производной.
Укажите тип с существующим объектом контроллера - укажите базовый контроллер Cbase аргумент для pidTuner при открытии тюнера PID. PID-тюнер проектирует контроллер того же типа, что и Cbase. Например, предположим C0 является pid объект контроллера, имеющий только пропорциональное и производное действие (контроллер PD). Затем, pidTuner(G,C0) открывает PID-тюнер с первоначальной конструкцией, которая является контроллером PD.
Укажите тип контроллера в приложении - В тюнере PID используйте меню Тип для изменения типов контроллера.

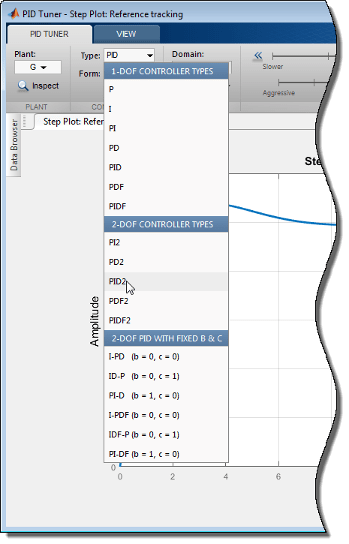
Для получения дополнительной информации о конкретных типах контроллеров, доступных в приложении PID Tuner:

Задача интерактивного редактора контроллера PID Tune

В задаче «Настройка контроллера PID» в интерактивном редакторе можно указать тип контроллера с помощью меню «Степени свободы» и «Тип контроллера».

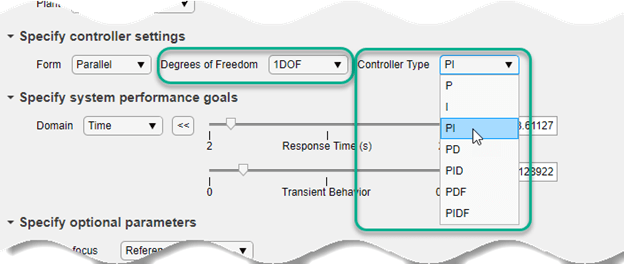
Для получения дополнительной информации о конкретных типах контроллеров, доступных в задаче Tune PID Controller, см.:

1-DOF Контроллеры

Следующая таблица суммирует контроллер PID с 1 финансовым департаментом типы, доступные со всеми инструментами, и приводится представительные формулы диспетчера для параллельной формы. Формулы стандартной формы и дискретного времени аналогичны.

Напечатать	Действия контроллера	Формула контроллера непрерывного времени (параллельная форма)	Формула контроллера дискретного времени (параллельная форма, метод интеграции ForwardEuler)
`P`	Только пропорциональный	_Kp	_Kp
`I`	Только интегральный	$\frac{_{}}{Kis}$	$_{} \frac{_{}}{КиЦз −}$ 1
`PI`	Пропорциональный и интегральный	$_{Кп} \frac{+_{}}{}$ Кис	$_{Кп} +_{} \frac{_{}}{КиЦз}$ − 1
`PD`	Пропорциональная и производная	$_{Kp} +_{}$ Kds	$_{Кп} +_{} \frac{Кдз}{_{-}}$ 1Ц
`PDF`	Пропорциональная и производная с фильтром первого порядка на члене производной	$_{Kp} \frac{+_{}}{_{} KdsTfs}$ + 1	$_{Кп} +_{} \frac{}{_{} \frac{{Kd1Tf}_{}}{+}}$ Цз − 1
`PID`	Пропорциональная, интегральная и производная	$_{Kp} \frac{+_{}}{} {Kis}_{} +$ Kds	$_{Кп} +_{} \frac{_{}}{КиЦз} -_{} \frac{1 +}{_{}}$ Кдз − 1Ts
`PIDF`	Пропорциональная, интегральная и производная с фильтром первого порядка на члене производной	$_{Kp} \frac{+_{}}{} \frac{{Kis}_{} +}{_{}}$ KdsTfs + 1	$_{Кп} +_{} \frac{_{}}{КиЦз} -_{} \frac{1}{_{+} \frac{_{}}{Kd1Tf}}$ + Цз − 1

2-DOF Контроллеры

Настраивающие инструменты могут автоматически проектировать контроллер PID с 2 финансовыми департаментами типы со свободными весами заданного значения. В следующей таблице представлены типы контроллеров 2-DOF, доступные во всех инструментах, а также репрезентативные формулы контроллеров для параллельной формы. Формулы стандартной формы аналогичны. Дополнительные сведения о 2-DOF контроллеров PID в целом см. в разделе Двухстепенные контроллеры PID.

Напечатать	Действия контроллера	Формула контроллера непрерывного времени (параллельная форма)	Формула контроллера дискретного времени (параллельная форма, метод интеграции ForwardEuler)
`PI2`	2-DOF пропорциональный и интегральный	$u =_{} Kp (br \frac{-_{}}{y}) +$ Kis (r − y)	$u =_{} Kp (br -_{} \frac{y_{)}}{+} KiTsz$ − 1 (r − y)
`PD2`	2-DOF пропорциональная и производная	$u =_{} Kp (br -_{} y) +$ Kds (cr − y)	$u =_{} Kp (br -_{} \frac{y)}{+_{}} Kdz -$ 1Ts (cr − y)
`PDF2`	2-DOF пропорциональная и производная с фильтром первого порядка на член производной	$u =_{} Kp (br -_{} \frac{y}{)_{} +} KdsTfs$ + 1 (cr − y)	$u =_{} Kp (br -_{} \frac{y}{)_{} + \frac{_{}}{}} Kd1Tf +$ Tsz − 1 (cr − y)
`PID2`	2-DOF пропорциональная, интегральная и производная	$u =_{} Kp (br \frac{-_{}}{y}) + {Kis}_{} (r - y)$ + Kds (cr − y)	$u =_{} Kp (br -_{} \frac{y_{)}}{+} KiTsz -_{} \frac{1 (}{r_{}} - y) +$ Kdz − 1Ts (cr − y)
`PIDF2`	2-DOF пропорциональная, интегральная и производная с фильтром первого порядка на члене производной	$u =_{} Kp (br \frac{-_{}}{y}) + {Kis}_{} \frac{(}{r_{} - y}) +$ KdTfs + 1 (cr − y)	$u =_{} Kp (br -_{} \frac{y_{)}}{+} KiTsz -_{} \frac{1}{_{(} r \frac{_{-}}{y)}} +$ Kd1Tf + Tsz − 1 (cr − y)

2-DOF Контроллеры с фиксированными весами уставки

При управлении PID ступенчатые изменения в опорном сигнале могут вызвать всплески в управляющем сигнале, вносимые пропорциональным и производным терминами. Путем фиксации весов уставок контроллера 2-DOF можно уменьшить влияние на управляющий сигнал, оказываемое изменениями опорного сигнала. Например, рассмотрите отношения между исходными данными r (заданное значение) и y (обратная связь) и продукция u (управляющий сигнал) непрерывно-кратного диспетчера PID с 2 финансовыми департаментами.

$u =_{} Kp (br \frac{-_{}}{y}) + {Kis}_{} (r - y)$ + Kds (cr − y)

Если задать b = 0 и c = 0, то изменения в уставке r не будут подаваться непосредственно на пропорциональные или производные члены в u. Контроллер b = 0, c = 0 называется контроллером типа I-PD. Контроллеры I-PD также полезны для улучшения отбраковки возмущений.

Тюнер PID и pidtune может разработать типы контроллеров с фиксированной уставкой и весом, приведенные в следующей таблице. Формулы стандартной формы и дискретного времени аналогичны.

Напечатать	Действия контроллера	Формула контроллера непрерывного времени (параллельная форма)	Формула контроллера дискретного времени (параллельная форма, метод интеграции ForwardEuler)
`I-PD`	2-DOF PID с b = 0, c = 0	$u =_{-} \frac{_{Kpy}}{} + Kis (_{r} -$ y) − Kdsy	$u =_{-}_{Kpy} \frac{_{+}}{} KiTsz - 1_{} \frac{(r}{-_{}} y$ ) − Kdz − 1Tsy
`I-PDF`	2-DOF PIDF с b = 0, c = 0	$u =_{-} \frac{_{Kpy}}{} + Kis (_{r} \frac{}{-_{} y)} -$ KdTfs + 1y	$u =_{-}_{Kpy} \frac{_{+}}{} KiTsz - 1_{} \frac{(}{r_{} - \frac{_{y}}{) −}}$ Kd1Tf + Tsz − 1y
`ID-P`	2-DOF PID с b = 0, c = 1	$u =_{-} \frac{_{Kpy}}{} + Kis (_{r} - y)$ + Kds (r − y)	$u =_{-}_{Kpy} \frac{_{+}}{} KiTsz - 1_{} \frac{(r}{-_{}} y) +$ Kdz − 1Ts (r − y)
`IDF-P`	2-DOF PIDF с b = 0, c = 1	$u =_{-} \frac{_{Kpy}}{} + Kis (_{r} \frac{}{-_{} y)} +$ KdTfs + 1 (r − y)	$u =_{-}_{Kpy} \frac{_{+}}{} KiTsz - 1_{} \frac{(}{r_{} - \frac{_{y}}{) +}}$ Kd1Tf + Tsz − 1 (r − y)
`PI-D`	2-DOF PID с b = 1, c = 0	$u =_{} Kp (r \frac{-_{}}{y}) + {Kis}_{} (r$ − y) − Kdsy	$u =_{} Kp (r -_{} \frac{y_{)}}{+} KiTsz -_{} \frac{1 (}{r_{}} -$ y) − Kdz − 1Tsy
`PI-DF`	2-DOF PIDF с b = 1, c = 0	$u =_{} Kp (r \frac{-_{}}{y}) + {Kis}_{} \frac{(}{r_{} - y})$ − KdTfs + 1y	$u =_{} Kp (r -_{} \frac{y_{)}}{+} KiTsz -_{} \frac{1}{_{(} r \frac{_{-}}{y)}}$ − Kd1Tf + Tsz − 1y

См. также

Функции

pidtune | pidTuner

Задачи интерактивного редактора

Настройка контроллера PID

Документация