Алгоритм настройки PID для линейной модели установки
C = pidtune(sys,type)
C = pidtune(sys,C0)
C = pidtune(sys,type,wc)
C = pidtune(sys,C0,wc)
C = pidtune(sys,...,opts)
[C,info] = pidtune(...)
C = pidtune(sys,type)type для завода sys. Если type задает PID-контроллер с одной степенью свободы (1-DOF), затем контроллер предназначен для контура обратной связи блока, как показано:
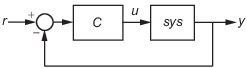
Если type задает контроллер PID с двумя степенями свободы (2-DOF), затем pidtune конструирует контроллер 2-DOF, как в контуре обратной связи этой иллюстрации:
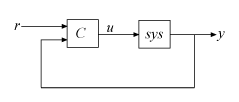
pidtune настраивает параметры PID-контроллера C сбалансировать производительность (время отклика) и надежность (пределы устойчивости).
C = pidtune(sys,C0)C0. Если sys и C0 являются дискретно-временными моделями, C имеет те же дискретные формулы интегратора, что и C0.
C = pidtune(sys,type,wc)C = pidtune(sys,C0,wc)wc для первой частоты пересечения коэффициента усиления 0 дБ отклика с разомкнутым контуром.
C = pidtune(sys,...,opts)pidtuneOptions для задания набора опций opts.
[ возвращает структуру данных C,info] = pidtune(...)info, которая содержит информацию о стабильности с замкнутым контуром, выбранной частоте пересечения усиления с разомкнутым контуром и фактическом поле фазы.
|
Однопроводная модель динамической системы установки для проектирования контроллера.
Если растение имеет неустойчивые полюса, и
вы должны использовать |
|
Тип разрабатываемого контроллера, указанный как символьный вектор. Термин тип контроллера обозначает, какие термины присутствуют в действии контроллера. Например, PI-контроллер имеет только пропорциональный и интегральный член, в то время как PIDF-контроллер содержит пропорциональные, интеграторные и отфильтрованные производные члены. 1-DOF Контроллеры
2-DOF Контроллеры
Дополнительные сведения о 2-DOF контроллеров PID в целом см. в разделе Двухстепенные контроллеры PID. 2-DOF Контроллеры с фиксированными весами уставки
Для более подробной информации о фиксированном весе заданного значения диспетчеры PID с 2 финансовыми департаментами посмотрите диспетчера PID Тайпеса для Настройки. Форма контроллераПри использовании Если Для получения дополнительной информации о формах и формулах контроллера МТС см.:
|
|
Параметры настройки контроллера МТС проектируемого контроллера, указанные как
|
|
Целевое значение частоты пересечения коэффициента усиления 0 дБ настроенного отклика с разомкнутым контуром. Определить Увеличение |
|
Набор опций, задающий дополнительные параметры настройки для |
|
Контроллер, предназначенный для Форма контроллера:
Тип контроллера:
Однако в любом случае, когда алгоритм может достичь адекватной производительности и надежности с использованием контроллера более низкого порядка, чем указано в Временная область:
При указании |
|
Структура данных, содержащая информацию о производительности и надежности настроенного цикла PID. Поля
Если |
В этом примере показано, как спроектировать PID-контроллер для установки, указанный в:
1) 3.
В качестве первого прохода создайте модель установки и сконструируйте для нее простой PI-контроллер.
sys = zpk([],[-1 -1 -1],1);
[C_pi,info] = pidtune(sys,'PI')C_pi =
1
Kp + Ki * ---
s
with Kp = 1.14, Ki = 0.454
Continuous-time PI controller in parallel form.
info = struct with fields:
Stable: 1
CrossoverFrequency: 0.5205
PhaseMargin: 60.0000
C_pi является pid объект контроллера, представляющий контроллер PI. Поля info показывают, что алгоритм настройки выбирает частоту пересечения с разомкнутым контуром около 0,52 рад/с.
Осмотрите закольцованную ступенчатую реакцию (эталонное сопровождение) контролируемой системы.
T_pi = feedback(C_pi*sys, 1); step(T_pi)

Чтобы увеличить время отклика, можно установить более высокую целевую частоту пересечения, чем результат, pidtune автоматически выбирает, 0,52. Увеличьте частоту пересечения до 1,0.
[C_pi_fast,info] = pidtune(sys,'PI',1.0)C_pi_fast =
1
Kp + Ki * ---
s
with Kp = 2.83, Ki = 0.0495
Continuous-time PI controller in parallel form.
info = struct with fields:
Stable: 1
CrossoverFrequency: 1
PhaseMargin: 43.9973
Новый контроллер достигает более высокой частоты пересечения, но за счет уменьшенного запаса по фазе.
Сравните отклик шага с замкнутым контуром с двумя контроллерами.
T_pi_fast = feedback(C_pi_fast*sys,1); step(T_pi,T_pi_fast) axis([0 30 0 1.4]) legend('PI','PI,fast')

Это снижение производительности приводит к тому, что контроллер PI не имеет достаточно степеней свободы для достижения хорошего запаса по фазе при частоте пересечения 1,0 рад/с. Добавление производного действия улучшает реакцию.
Проектирование контроллера PIDF для Gc с целевой частотой пересечения 1,0 рад/с.
[C_pidf_fast,info] = pidtune(sys,'PIDF',1.0)C_pidf_fast =
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 2.72, Ki = 0.985, Kd = 1.72, Tf = 0.00875
Continuous-time PIDF controller in parallel form.
info = struct with fields:
Stable: 1
CrossoverFrequency: 1
PhaseMargin: 60.0000
Поля информации показывают, что производное действие в контроллере позволяет алгоритму настройки разработать более агрессивный контроллер, который достигает целевой частоты пересечения с хорошим запасом фазы.
Сравните ступенчатую реакцию с замкнутым контуром и отклонение возмущений для быстрых контроллеров PI и PIDF.
T_pidf_fast = feedback(C_pidf_fast*sys,1); step(T_pi_fast, T_pidf_fast); axis([0 30 0 1.4]); legend('PI,fast','PIDF,fast');

Можно сравнить отклонение входных помех (нагрузки) контролируемой системы с контроллерами быстрого PI и PIDF. Для этого постройте график реакции функции передачи с замкнутым контуром от входа завода к выходу завода.
S_pi_fast = feedback(sys,C_pi_fast); S_pidf_fast = feedback(sys,C_pidf_fast); step(S_pi_fast,S_pidf_fast); axis([0 50 0 0.4]); legend('PI,fast','PIDF,fast');

Этот график показывает, что контроллер PIDF также обеспечивает более быстрое отклонение возмущений.
Проектирование контроллера МТС в стандартной форме для установки, определенной
1) 3.
Чтобы создать контроллер в стандартной форме, используйте контроллер стандартной формы в качестве C0 аргумент для pidtune.
sys = zpk([],[-1 -1 -1],1); C0 = pidstd(1,1,1); C = pidtune(sys,C0)
C =
1 1
Kp * (1 + ---- * --- + Td * s)
Ti s
with Kp = 2.18, Ti = 2.36, Td = 0.591
Continuous-time PID controller in standard form
Разработка дискретно-временного PI-контроллера с использованием определенного метода для дискретизации интегратора.
Если установка находится в дискретном времени, pidtune автоматически возвращает контроллер дискретного времени с использованием метода интеграции Forward Euler по умолчанию. Чтобы указать другой метод интеграции, используйте pid или pidstd создание дискретно-временного контроллера, имеющего требуемый способ интегрирования.
sys = c2d(tf([1 1],[1 5 6]),0.1); C0 = pid(1,1,'Ts',0.1,'IFormula','BackwardEuler'); C = pidtune(sys,C0)
C =
Ts*z
Kp + Ki * ------
z-1
with Kp = -0.518, Ki = 10.4, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time PI controller in parallel form.
Используя C0 в качестве входных причин pidtune для проектирования контроллера C той же формы, типа и метода дискретизации, что и C0. На дисплее показано, что интегральный член C использует метод интеграции Backward Euler.
Укажите трапециевидный интегратор и сравните полученный контроллер.
C0_tr = pid(1,1,'Ts',0.1,'IFormula','Trapezoidal'); Ctr = pidtune(sys,C_tr)
Ctr =
Ts*(z+1)
Ki * --------
2*(z-1)
with Ki = 10.4, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time I-only controller.Спроектируйте 2-DOF PID-контроллер для установки с помощью передаточной функции:
5s + 0,1.
Используйте целевую полосу пропускания 1,5 рад/с.
wc = 1.5;
G = tf(1,[1 0.5 0.1]);
C2 = pidtune(G,'PID2',wc)C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 1.26, Ki = 0.255, Kd = 1.38, b = 0.665, c = 0
Continuous-time 2-DOF PID controller in parallel form.
Использование типа 'PID2' причины pidtune для создания контроллера 2-DOF, представленного в виде pid2 объект. Этот результат подтверждается на дисплее. На дисплее также показано, что pidtune настраивает все коэффициенты контроллера, включая веса уставок b и c, чтобы сбалансировать производительность и надежность.
По умолчанию pidtune с type ввод возвращает pid контроллер в параллельной форме. Чтобы создать контроллер в стандартной форме, используйте pidstd контроллер в качестве входного аргумента C0. Дополнительные сведения о формах параллельных и стандартных контроллеров см. в разделе pid и pidstd справочные страницы.
Для получения информации о интерактивной настройке PID в интерактивном редакторе см. задачу Настройка контроллера PID в интерактивном редакторе. Эта задача позволяет в интерактивном режиме проектировать контроллер PID и автоматически генерировать код MATLAB ® для сценария в реальном времени.
Сведения об алгоритме настройки PID MathWorks ® см. в разделе Алгоритм настройки PID.
Для получения информации о интерактивной настройке PID в интерактивном редакторе см. задачу Настройка контроллера PID в интерактивном редакторе. Эта задача позволяет в интерактивном режиме проектировать контроллер PID и автоматически генерировать код MATLAB для сценария в реальном времени. Пример см. в разделе Проектирование контроллера PID в интерактивном редакторе.
Для интерактивной настройки PID в автономном приложении используйте PID-тюнер. Пример разработки контроллера с помощью приложения см. в документе «Проектирование контроллера PID для быстрого отслеживания ссылок».
Oström, K. J. и Hägglund, T. Advanced PID Control, Research Triangle Park, NC: Instrumentation, Systems, and Automation Society, 2006.