dtmc объектная структура предоставляет базовые инструменты для моделирования и анализа дискретно-временных марковских цепей. Объект поддерживает цепочки с конечным числом состояний, которые развиваются за дискретное время с однородной по времени структурой перехода.
dtmc идентифицирует каждую цепь Маркова с помощью NumStatesоколо-NumStates матрица P перехода, не зависящая от начального состояния x0 или начального распределения состояний § 0. Можно указать P как правую стохастическую матрицу или матрицу эмпирических подсчетов.
В качестве правой стохастической матрицы:
Пидж - неотрицательная вероятность перехода из состояния i в состояние j.
Каждая строка суммы P равна 1.
securitytP описывает эволюцию распределения состояний от времени t к времени t + 1.
Распределение состояний в момент времени t, ¼ t - вектор строки длины NumStates.
В качестве матрицы эмпирических подсчетов Pij представляет собой наблюдаемое число раз, когда состояние i переходит в состояние j. dtmc объект нормализует строки P так, чтобы это была правостохастическая матрица.
mcmix функция является альтернативным создателем объекта цепи Маркова; он генерирует цепочку с заданным нулевым шаблоном и вероятностями случайного перехода. mcmix хорошо подходит для создания цепей с различным временем смешивания для целей тестирования.
Чтобы визуализировать направленный граф или диграф, связанный с цепью, используйте graphplot объектная функция. graphplot аналогичен plot объектная функция MATLAB
®digraph объект, но он включает в себя дополнительные функциональные возможности для анализа структуры цепи Маркова. Настройки параметров выделяют сообщающиеся классы (то есть сильно связанные компоненты диграфа) и специфические характеристики, влияющие на сходимость, такие как повторяемость, переходность и периодичность. Можно выделить вероятности перехода в P, раскрашивая ребра графика с помощью интенсивностей тепловых карт.
Для визуализации крупномасштабной структуры в цепочке, graphplot может конденсировать передаваемые классы к репрезентативным узлам. Эта опция основана на condensation объектная функция digraph объект.
classify объектная функция - числовой аналог выделения класса в графе. classify возвращает характеристики сообщающихся классов, которые определяют ограничивающее поведение. Классификация состояний объединяет теоретические алгоритмы, такие как bfsearchфункция объекта MATLAB (поиск по ширине) graph объект, но с более прямыми матричными вычислениями, специфичными для теории цепи Маркова. subchain способ позволяет извлекать из цепочки конкретные сообщающиеся классы для дальнейшего анализа.
isreducible и isergodic объектные функции дают краткие сводки структуры цепи. В совокупности они обеспечивают необходимые и достаточные условия для существования уникального ограничивающего распределительного , где и для каждого начального распределения ¼ 0. asymptotics объектная функция вычисляет , если она существует, и оценивает время смешения с помощью анализа собственных значений. eigplot объектная функция отображает собственные значения P. На этом рисунке показан пример графика собственных значений, возвращаемого eigplot.
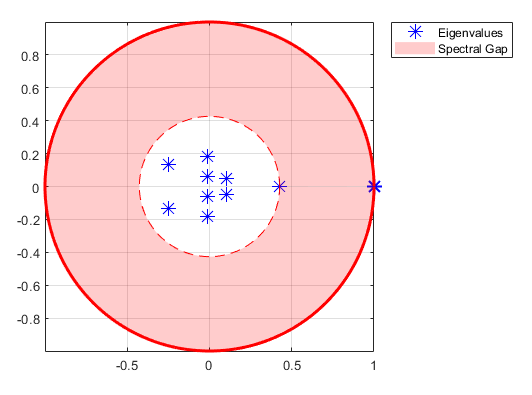
Одним из препятствий на пути сближения является периодичность. lazy функция объекта устраняет периодичность путем регулирования инерции состояния (то есть взвешивания диагональных элементов Р) для получения заданных величин «лени» в цепи. Эти преобразования не влияют на ограничивающие распределения.
simulate и redistribute объектные функции обеспечивают реализацию процесса по мере его развития из заданного начального состояния или распределения. simplot и distplot функции объекта обеспечивают различные визуализации. Этот рисунок является примером графика распределения, показывающего эволюцию распределения состояний, начиная с равномерного распределения начальных состояний.
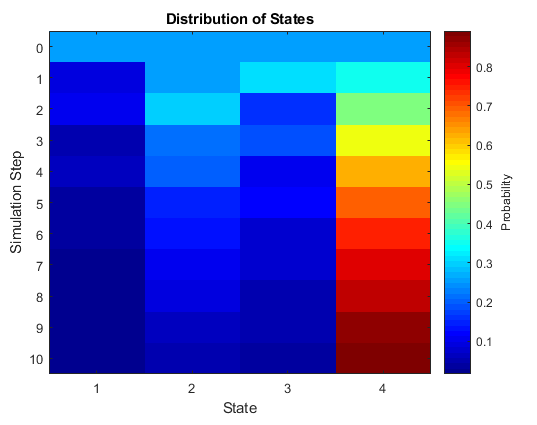
Создать объект модели цепи Маркова можно двумя способами:
Определите соответствующие дискретные состояния в процессе, а затем оцените вероятности перехода между ними. В простейшем случае теория предполагает структуру цепи и матрицу перехода P. В этой ситуации вас интересует прежде всего то, как теория отыгрывается на практике - то, что не всегда очевидно из теории. Как только вы знаете P, создайте объект цепи Маркова, передав P dtmc, который реализует теоретическую цепочку.
Если у вас меньше конкретной информации о процессе, то для воспроизведения эмпирических результатов необходимо поэкспериментировать с различным количеством состояний и возможных шаблонов перехода. mcmix функция обеспечивает понимание скелетной структуры цепи, которая может фиксировать существенные особенности в данных. С помощью итеративного процесса можно настроить случайно сгенерированную матрицу P перехода в соответствии с целями моделирования.
Для строителя эконометрической модели наиболее важным следствием выбора P является асимптотическое поведение цепи. Чтобы понять это поведение, идентифицируйте и отделяйте переходные состояния (те состояния, чьи вероятности времени возврата переходят в ноль асимптотически) от повторяющихся состояний (те состояния, чьи вероятности времени возврата переходят в один асимптотически). Переходность и повторяемость являются свойствами, общими для всех состояний в связном классе. Чтобы визуально определить, являются ли состояния переходными или повторяющимися, передайте объект цепи Маркова в graphplot объектная функция и указать 'ColorNodes',true. В качестве альтернативы, выходы classify функция объекта предоставляет числовые инструменты для оценки. Этот рисунок является примером диграфа с классифицированными узлами.
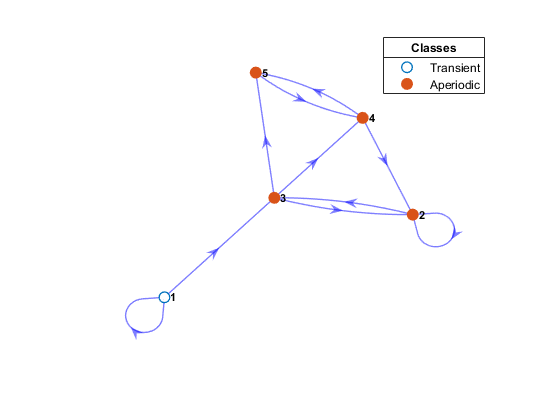
Сжатый вид диграфа упрощает эту оценку, объединяя каждый сообщающийся класс в «суперноду». В конденсированном графе можно легко распознать транзит и рецидив по степени выхода супернода (степень выхода больше 0 подразумевает транзит). Неприводимые цепи состоят из одного, обязательно повторяющегося, сообщающегося класса. Unichains состоят из одного повторяющегося класса и любого числа спутниковых переходных классов. Унихины поддерживают желаемое ограничивающее поведение неприводимой цепи. Рассмотрение конденсированного графа часто является предшественником обрезки цепочки неактуальных переходных состояний. subchain функция обрезает цепочки переходных классов. Эта фигура представляет собой сжатый вид диграфа на предыдущей фигуре.
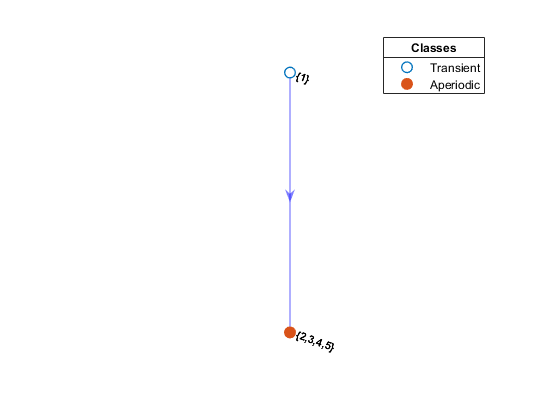
Двумя основными препятствиями к единообразному ограничительному поведению являются:
Редуктивность, существование более одного класса связи
Периодичность, тенденция к циклу между подклассами в рамках одного класса
Комбинация graphplot и classify функции объекта могут идентифицировать эти проблемы. Если цепь редуцируема, а не унихайна, обычно разбивают анализ между независимыми повторяющимися классами или полностью переформулируют цепь. Если цепочка является периодической (то есть содержит периодический повторяющийся класс), но общая структура фиксирует существенные детали приложения, lazy функция объекта обеспечивает исправление. Ленивые цепи возмущают диагональные элементы P, чтобы исключить периодичность, оставляя асимптотику без влияния.
isreducible и isergodic функции объекта суммируют классификацию состояний. Каждая цепь имеет стационарный
распределительный π∗, где π∗=π∗Pв P является стохастическим и имеет собственное значение единицы. Если цепь неприводима, стационарное распределение является уникальным. Однако неприводимость, хотя и достаточна, не является необходимым условием уникальности. Унихин также приводит к уникальному стационарному распределению, имеющему нулевую массу вероятности в переходных состояниях. В этой связи анализ классификации состояний имеет важное значение, поскольку isreducible прибыль true только если цепочка в целом состоит из одного сообщающегося класса. isreducible прибыль false для произвольных унихин, в этом случае необходимо решить, являются ли переходные классы релевантной частью модели.
Эргодичность, или примитивность, - это сочетание неприводимости и апериодичности. Эргодическая цепочка имеет уникальное предельное распределение, то есть ¼ 0 сходится к для каждого начального распределения ¼. Определить, является ли цепь в целом эргодичной, можно с помощью isergodic. Функция идентифицирует эргодические унихины путем оценки единственного повторяющегося класса. Цепь является периодической, если она неприводима и не эргодична, то есть если ~tfirreduc + ~tfergo = false, где tfirreduc и tfergo возвращаются isreducible и isergodicсоответственно.
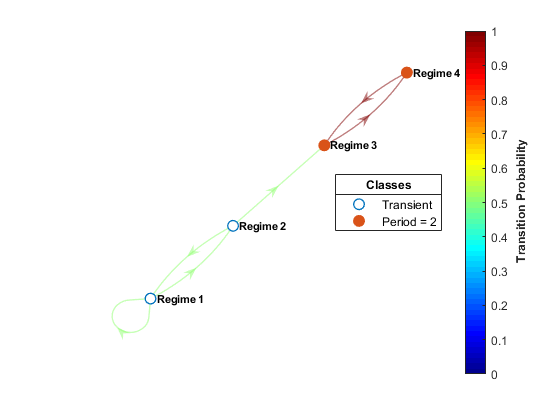
После подтверждения того, что цепь эргодична, можно определить уникальное ограничивающее распределение с помощью asymptotics объектная функция. asymptotics возвращает предельное распределения и оценку времени смешения, которое является постоянной времени для затухания переходного поведения. Теорема Перрона - Фробениуса для неприводимых неотрицательных матриц (см. [1]) полезна для интерпретации этих результатов. Любая стохастическая матрица имеет спектральный радиус, равный единице. Периодические матрицы периода k имеют k собственных значений, равномерно распределенных по единичной окружности в k корнях единицы. Величина наибольшего собственного значения внутри единичной окружности определяет скорость затухания переходных состояний. eigplot функция объекта обеспечивает быструю визуализацию этой информации. Эта цифра представляет собой график собственных значений марковской цепи с периодом три.
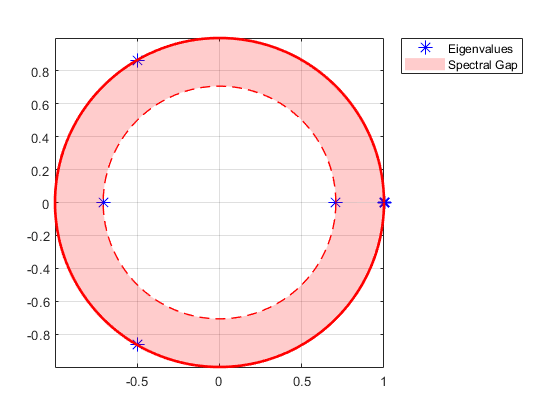
Независимо от асимптотических свойств цепи, можно изучить скорость ее смешивания, применив анализ конечных стадий. hitprob и hittime функции возвращают вероятности попадания и ожидаемые времена первого попадания для подмножества целевых состояний, начиная с каждого состояния в цепочке. Обе функции дополнительно выводят на график диграф с цветами узлов, задающими вероятности или время попадания. На этом рисунке показан пример диграфа с цветами узлов, указывающими ожидаемое время первого попадания. Диграф также указывает, являются ли начальные состояния удаленными для целевого объекта.
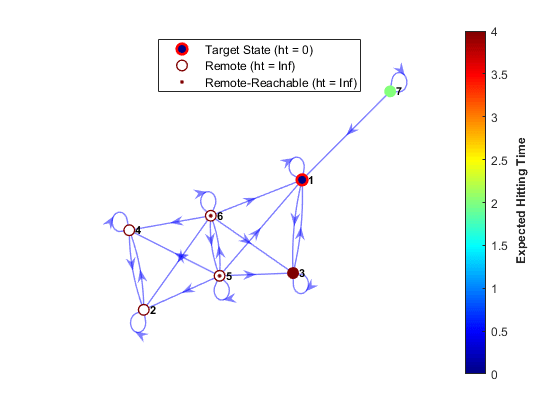
Моделирование и перераспределение позволяют генерировать на цепочке статистическую информацию, которую трудно вывести непосредственно из теории. simulate и simplot функции объекта и redistribute и distplot функции объекта, предоставление вычислительных и графических инструментов для такого анализа. simulate, например, генерирует независимые случайные ходы по цепочке. Как и с simulate и объектные функции в других разделах Econometrics Toolbox™, усреднения зависимой статистики играют важную роль в прогнозировании. Передача simplot функция объекта предлагает несколько подходов к визуализации. Эта цифра показывает долю состояний, посещенных после 100 случайных ходов длиной 10 шагов через периодическую цепочку Маркова на предыдущем рисунке.
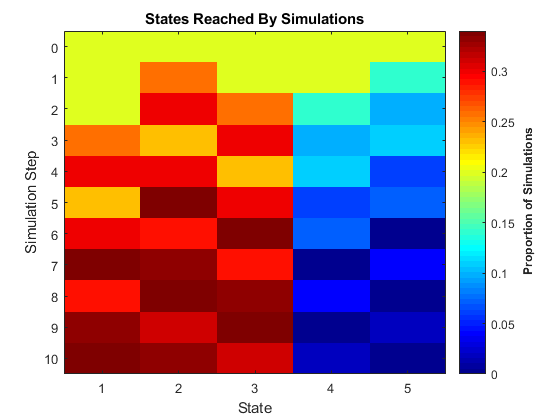
[1] Рог, R. и К. Р. Джонсон. Матричный анализ. Кембридж, Великобритания: Cambridge University Press, 1985.
bfsearch | condensation | graphplot | mcmix