Преобразование запаса усиления на основе диска в размер диска и перекос
umargin и diskmargin модельное усиление и изменение фазы как мультипликативный коэффициент F (s), принимающий значения на диске с центром на реальной оси. Диск описывается двумя параметрами: ɑ, устанавливающим размер вариации, и λ, или перекос, смещающий вариацию усиления в сторону увеличения или уменьшения. (Дополнительные сведения об этой модели см. в разделе Алгоритмы.) Диск в качестве альтернативы может быть описан по его перехватам по реальной оси.DGM = [gmin,gmax], которые представляют относительную величину изменения коэффициента усиления вокруг номинального значения F = 1. Использовать gm2dm и dm2gm для преобразования между ɑ,σ значениями и запасом усиления на основе диска DGM = [gmin,gmax] которые описывают один и тот же диск.
Вычислите размер диска α диска, который представляет изменение коэффициента усиления ± 6 дБ, то есть коэффициент усиления, который может увеличиться или уменьшиться примерно в 2 раза.
GM = db2mag(6); [alpha,sigma] = gm2dm(GM)
alpha = 0.6646
sigma = 0
Для вариаций симметричного усиления - перекос sigma равно 0. Проверьте диск, соответствующий этому изменению коэффициента усиления.
diskmarginplot(alpha,sigma,'disk')
Диск, который фиксирует изменения коэффициента усиления в два раза в любом направлении, также моделирует изменения фазы ± 37 °.
Определите размер и наклон диска, необходимые для фиксации изменений коэффициента усиления от 80% до 150% от номинального, а также изменения фазы от -20 до + 40 градусов. Во-первых, использоватьgetDGM найти DGM = [gmin,gmax] описывает диск, который захватывает эти целевые диапазоны.
DGM = getDGM([0.8,1.5],[-20,40],'tight')DGM = 1×2
0.2031 1.5000
Теперь используйте gm2dm чтобы преобразовать эту дисковую вариацию усиления в α, λ параметризацию диска .
[alpha,sigma] = gm2dm(DGM)
alpha = 0.6145
sigma = -1.7451
Для смоделированного усиления и фазовых изменений наклон меньше нуля, поскольку диапазон усиления на основе диска DGM = [0.2 1.5] включает в себя большее уменьшение усиления, чем увеличение.
diskmarginplot(alpha,sigma,'disk')
Определите размер и наклон дисков, которые захватывают диапазоны усиления [0,2,1,3], [0,5,2] и [0,8,3].
GainRange1 = [0.2,1.3]; GainRange2 = [0.5,2]; GainRange3 = [0.8,3];
Для указанных выше диапазонов усиления вычислите запас усиления на основе диска.
[alpha,sigma] = gm2dm([GainRange1;GainRange2;GainRange3])
alpha = 3×1
0.4364
0.6667
0.3636
sigma = 3×1
-3.0833
0
3.5000
Для вектора sigma, первая запись отрицательна, поскольку первая запись DGM имеет смещение в сторону уменьшения усиления. Аналогично, второй вход равен нулю из-за сбалансированной вариации усиления, а третий вход является положительным из-за смещения в сторону увеличения усиления. На графике показаны диски, соответствующие диапазону изменений коэффициента усиления, указанному выше.
diskmarginplot(alpha,sigma,'disk')
umargin и diskmargin моделируют усиление и фазовые изменения в отдельном канале обратной связи в качестве частотно-зависимого мультипликативного коэффициента F (s), умножающего номинальный отклик с разомкнутым контуром L (s), так что возмущенный отклик равен L (s) F (s). Коэффициент F (ы) параметризуется следующим образом:
В этой модели
δ (s) - динамическая неопределенность, ограниченная коэффициентом усиления, нормализованная таким образом, что она всегда изменяется в пределах единичного диска (||δ||∞ < 1).
ɑ устанавливает величину усиления и изменения фазы, смоделированную F. Для фиксированного λ параметр ɑ управляет размером диска. Для ɑ = 0 мультипликативный коэффициент равен 1, что соответствует номинальному L.
, называемый перекосом, смещает смоделированную неопределенность в сторону увеличения или уменьшения усиления.
Коэффициент F принимает значения на диске, центрированном по реальной оси и содержащем номинальное значение F = 1. Диск характеризуется своим перехватом DGM = [gmin,gmax] с действительной осью. gmin < 1 и gmin > 1 - минимальное и максимальное относительные изменения коэффициента усиления, смоделированные по F, на номинальной фазе. Фазовая неопределенность, смоделированная F, представляет собой диапазон DPM = [-pm,pm] фазовых значений при номинальном усилении (| F | = 1). Например, на следующем графике справа показан диск F, пересекающий действительную ось в интервале [0.71.1.4]. В левой части показано, что этот диск моделирует вариацию усиления ± 3 дБ и вариацию фазы ± 19 °.
DGM = [0.71,1.4]
F = umargin('F',DGM)
plot(F)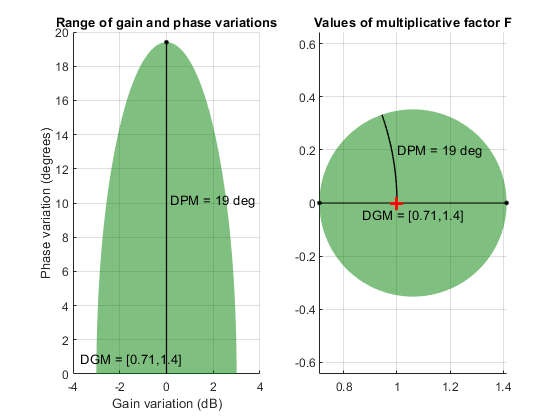
gm2dm и gm2dm преобразует между этими двумя способами задания диска мультипликативного усиления и фазовой неопределенности: диапазон изменения усиления вида DGM = [gmin,gmax]и ɑ,σ параметризацию соответствующего диска.
Дополнительные сведения о модели неопределенности для изменений коэффициента усиления и фазы см. в разделе Анализ стабильности с использованием полей диска.
diskmargin | diskmarginplot | dm2gm | getDGM | umargin