Для анализа влияния параметров и состояний (совместно называемых параметрами) модели Simulink ® на требования к конструкции сигналов модели сначала генерируются выборки параметров. Затем необходимо определить функцию затрат путем создания требования к конструкции для сигналов модели и оценить функцию затрат для каждого образца. Наконец, анализируется взаимосвязь между вариациями параметров и значениями функции затрат. Этот анализ можно выполнить следующими способами:
Просмотрите график анализа функции затрат по образцам параметров для определения тенденций. Этот метод является неформальным и обеспечивает визуальную интуицию о том, как различные параметры влияют на функцию затрат.
В анализаторе чувствительности после завершения оценки в приложении генерируется график рассеяния результатов оценки. График отображает вычисленное значение функции затрат как функцию каждого параметра в наборе параметров. В последнем вложенном графике столбца отображается распределение вероятностей вычисленных значений функции затрат. Можно добавить линию наилучшего вписывания к подсчетам разброса, щелкнув правой кнопкой мыши на графике и выбрав в контекстном меню пункт «Наложение линейного вписывания». На этом графике линия наилучшего вписывания указывает, что Gain параметр оказывает большое влияние на требование.
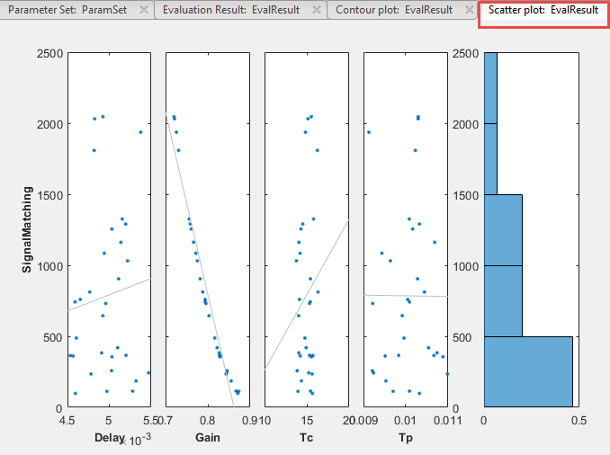
Можно также вывести на график контурный график вычисленных результатов. Дополнительные сведения об этих графиках см. в разделе Взаимодействие с графиками в анализаторе чувствительности. Пример см. в разделе Определение ключевых параметров для оценки (GUI).
В командной строке можно использовать следующие инструменты:
sdo.scatterPlot - График разброса выборок параметров по оценке функции затрат
surf, mesh, contour - 3-D график выборок двух параметров по оценке функции затрат
Пример см. в разделе Определение ключевых параметров для оценки (код).
Помимо визуального анализа влияния параметров на функцию затрат, можно также вычислить статистику для количественной оценки отношения.
Получение сводной статистики о взаимосвязи между оценками функций затрат и выборками параметров. Доступные методы анализа включают в себя:
| Метод | Описание |
|---|---|
| Корреляция | Используется для анализа корреляции параметров модели и выходных данных функции затрат. |
| Частичная корреляция | Используйте для анализа корреляции параметра модели и функции затрат, устраняя эффекты остальных параметров. |
| Стандартизированная регрессия | Используйте, если предполагается, что параметры модели линейно влияют на функцию затрат. |
Для каждого из этих методов можно указать, какие данные следует использовать для анализа, выбрав один из следующих типов анализа:
Линейный анализ, также называемый анализом Пирсона - использует необработанные данные для анализа. Линейный анализ используется при ожидаемом линейном соотношении между параметрами и функцией затрат, а также при нормальном распределении остатков относительно линии наилучшего вписывания. Также рекомендуется линейный анализ, когда количество выборок и, следовательно, количество остаточных точек велико.
Ранжированный анализ, также называемый анализом Спирмена и ранжированным преобразованием - использует ранги данных для анализа. Ранжированный анализ используется, когда ожидается нелинейное монотонное отношение между параметрами и функцией затрат и когда остатки относительно линии наилучшего вписывания обычно не распределены. Ранжированный анализ также рекомендуется, когда количество образцов, и поэтому количество остаточных точек мало.
Линейный анализ сохраняет информацию о интервалах между значениями данных, в то время как ранжированный анализ не содержит. Предположим, что у вас был следующий набор данных:
| x1 | x2 | y |
|---|---|---|
| 9 | 20 | 340 |
| 5 | 60 | 106 |
| 2.3 | 50.4 | 870.5 |
Здесь x1 и x2 - параметры модели, а y - функция затрат. Каждая строка представляет выборку и соответствующую оценку функции затрат.
Данные ранжируются по столбцам. Например, при ранжировании данных в столбце 1 (x1), содержащем записи 9, 5 и 2.3, ранжированные данные равны 3, 2 и 1. Ранжированные наборы данных для выборок x1, x2 и y являются следующими:
| x1 | x2 | y |
|---|---|---|
| 3 | 1 | 2 |
| 2 | 3 | 1 |
| 1 | 2 | 3 |
Ранжированный набор данных может использоваться для корреляционного, частичного корреляционного или стандартизированного регрессионного анализа.
Вычисляют коэффициент ранговой корреляции Кендалла - Кендалла.
Применимо, если метод анализа - Корреляция. Требуется программное обеспечение для Toolbox™ статистики и машинного обучения.
Вычисляет коэффициенты корреляции, R. Используйте этот метод для анализа корреляции параметров модели и выходных данных функции затрат.
R рассчитывается следующим образом:
x содержит Ns выборок параметров Np-модели. y содержит Ns строк, каждая строка соответствует оценке функции затрат для образца в x.
Значения R находятся в диапазоне [-1 1]. (i, j) запись R указывает корреляцию между x (i) и y (j).
R(i,j) > 0 - Переменные имеют положительную корреляцию. Переменные увеличиваются вместе.
R(i,j) = 0 - Переменные не имеют корреляции.
R(i,j) < 0 - Переменные имеют отрицательную корреляцию. Когда одна переменная увеличивается, другая уменьшается.
Вычисляет коэффициенты частичной корреляции, R. Для этого метода требуется программное обеспечение Statistics and Machine Learning Toolbox. Этот метод используется для анализа корреляции параметра модели и функции затрат с корректировкой для устранения влияния других параметров.
R рассчитывается с использованием partialcorri (Statistics and Machine Learning Toolbox) из программного обеспечения Statistics and Machine Learning Toolbox.
Вычисляет стандартизированные коэффициенты регрессии R. Используйте этот метод, если предполагается, что параметры модели линейно влияют на функцию затрат.
R рассчитывается следующим образом:
bx
Рассмотрим одну выборку (x1,...,xNp) и соответствующий один выход, y. bx - вектор коэффициента регрессии, вычисленный с использованием наименьших квадратов при условии линейной модели. R стандартизирует каждый элемент bx, умножая его на отношение стандартного отклонения соответствующей х-выборки (
В анализаторе чувствительности после оценки требований к конструкции укажите методы и типы анализа на вкладке Статистика приложения.
Выберите результаты анализа в списке Результаты анализа для анализа. После этого необходимо указать методы и типы анализа и щелкнуть ![]() Вычислить статистику (Compute Statistics). Можно вычислить все применимые комбинации методов и типов анализа.
Вычислить статистику (Compute Statistics). Можно вычислить все применимые комбинации методов и типов анализа.
Результаты анализа возвращаются в StatsResult переменная, в области Результаты приложения. В этом случае StatsResult переменная включает в себя коэффициенты линейной корреляции (Пирсона) и коэффициенты линейной стандартизированной регрессии, вычисленные между функцией затрат и каждым параметром. Для просмотра коэффициентов щелкните правой кнопкой мыши StatsResultи выберите «Открыть» в контекстном меню.
Формируется график торнадо, отображающий результаты анализа в порядке влияния параметров на функцию затрат. Параметр, который в наибольшей степени влияет на функцию затрат, отображается вверху. Как было видно на графике рассеяния результатов, на этом графике торнадо Gain параметр оказывает наибольшее влияние на функцию затрат на требования к конструкции.
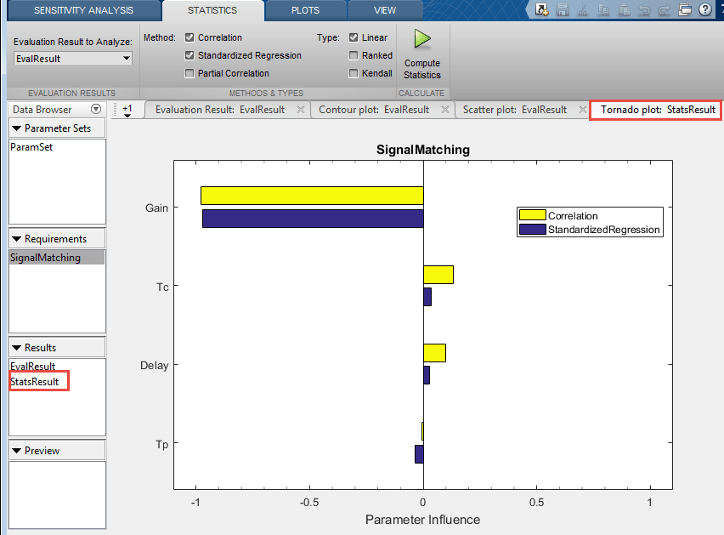
Дополнительные сведения о графиках торнадо см. в разделе Взаимодействие с графиками в анализаторе чувствительности. Пример см. в разделе Определение ключевых параметров для оценки (GUI).
В командной строке укажите методы и типы анализа с помощью sdo.analyze. Эта функция выполняет анализ линейной корреляции по умолчанию. Чтобы указать другие методы анализа, используйте sdo.AnalyzeOptions. Пример см. в разделе Определение ключевых параметров для оценки (код).
sdo.analyze | sdo.AnalyzeOptions | sdo.evaluate | sdo.sample