Настройка циклов обратной связи с фиксированной структурой
[G,C,gam]
= looptune(G0,C0,wc)
[G,C,gam]
= looptune(G0,C0,wc,Req1,...,ReqN)
[G,C,gam]
= looptune(...,options)
[G,C,gam,info]
= looptune(...)
[ настраивает цикл обратной связиG,C,gam]
= looptune(G0,C0,wc)
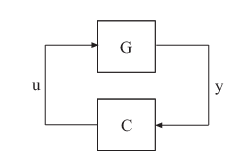
для удовлетворения следующих требований по умолчанию:
Шумовая полоса - перекрестный коэффициент усиления для каждого цикла падает в частотном интервале wc
Эффективность - Интегральное действие на частотах ниже wc
Робастность - Достаточные запасы устойчивости и наклон усиления на частотах выше wc
Настраиваемое genss модели C0 задает структуру контроллера, параметры и начальные значения. Модель G0 задает объект. G0 может быть числовой моделью LTI, или, для совместной настройки объекта управления и контроллера, настраиваемой genss модель. Сигналы датчика y (измерения) и сигналы привода u (управляет) задает контур между объектом и контроллером.
Примечание
Для настройки Simulink® модели с looptune, использование slTuner (Simulink Control Design), чтобы создать интерфейс к вашей модели Simulink. Затем можно настроить систему управления с looptune (Simulink Control Design) для slTuner (требует Simulink Control Design™).
[ настраивает цикл обратной связи, чтобы удовлетворить дополнительные требования проекта, указанные в одном или нескольких объектах цели настройки G,C,gam]
= looptune(G0,C0,wc,Req1,...,ReqN)Req1,...,ReqN. Опускание wc использовать требования, указанные в Req1,...,ReqN вместо явной целевой частоты среза и требований к эффективности и робастности по умолчанию.
[ задает дополнительные опции, включая целевой запас по амплитуде, целевой запас по фазе и вычислительные опции для алгоритма настройки.G,C,gam]
= looptune(...,options)
[ возвращает структуру G,C,gam,info]
= looptune(...)info с дополнительной информацией о настроенном результате. Использование info с loopview команда для визуализации ограничений настройки и проверки настроенного проекта.
|
Числовая модель LTI или настраиваемая Объект является фрагментом системы управления, выходами которой являются сигналы датчика (измерения) и входами которой являются сигналы привода (управления). Использовать |
|
Обобщенная модель LTI, представляющая контроллер. Контроллер является фрагментом вашей системы управления, которая получает сигналы датчика (измерения) в качестве входов и выдает сигналы привода (управления) в качестве выходов. Используйте Систему управления Blocks и Обобщенные модели LTI, чтобы представлять настраиваемые компоненты контроллера. Использовать |
|
Вектор, задающий целевую область пересечения Скалярное |
|
Один или несколько |
|
Набор опций для |
|
Настроенный объект. Если Если | ||||||
|
Настроенный контроллер. | ||||||
|
Параметр, указывающий на степень успеха при удовлетворении всех ограничений настройки. Значение Для достижения наилучших результатов используйте | ||||||
|
Данные для проверки результатов настройки, возвращенные как структура. Как использовать данные в
|
Настройте систему управления, представленную на следующем рисунке, чтобы добиться пересечения между 0,1 и 1 рад/мин.
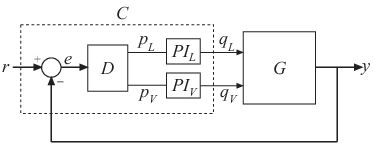
Устройство 2 на 2 объекты G представлен:
Контроллер с фиксированной структурой, C, включает три компонента: матрица развязки 2 на 2 D и два ПИ-контроллеров PI_L и PI_V. Сигналы r, y, и e являются векторными сигналами размерности 2.
Создайте числовую модель, которая представляет объект, и настраиваемую модель, которая представляет контроллер. Назовите все входы и выходы как на схеме, так что looptune знает, как соединить объект и контроллер через сигналы управления и измерения.
s = tf('s');
G = 1/(75*s+1)*[87.8 -86.4; 108.2 -109.6];
G.InputName = {'qL','qV'};
G.OutputName = 'y';
D = tunableGain('Decoupler',eye(2));
D.InputName = 'e';
D.OutputName = {'pL','pV'};
PI_L = tunablePID('PI_L','pi');
PI_L.InputName = 'pL';
PI_L.OutputName = 'qL';
PI_V = tunablePID('PI_V','pi');
PI_V.InputName = 'pV';
PI_V.OutputName = 'qV';
sum1 = sumblk('e = r - y',2);
C0 = connect(PI_L,PI_V,D,sum1,{'r','y'},{'qL','qV'});
wc = [0.1,1];
[G,C,gam,info] = looptune(G,C0,wc);C является настроенным контроллером, в данном случае a genss модель с теми же типами блоков, что и C0.
Вы можете изучить настроенный результат, используя loopview.
looptune автоматически преобразует целевую полосу пропускания, требования к эффективности и дополнительные требования проект в функции взвешивания, которые выражают требования как H∞ задачу оптимизации. looptune затем использует systune оптимизировать настраиваемые параметры для минимизации нормы H∞. Для получения дополнительной информации об алгоритмах оптимизации см. [1].
looptune вычисляет норму H∞ с помощью алгоритма [2] и сохраняющих структуру собственных преобразователей из библиотеки SLICOT. Дополнительные сведения о библиотеке SLICOT см. в разделе http://slicot.org.
Для настройки моделей Simulink с looptune, см. slTuner (Simulink Control Design) и looptune (Simulink Control Design) (требует Simulink Control Design).
[1] P. Apkarian and D. Noll, «Nonsmooth H-infinity Synthesis». Транзакции IEEE по автоматическому управлению, том 51, номер 1, 2006, стр. 71-86.
[2] Bruisma, N.A. and M. Steinbuch, «A Fast Algorithm to Compute the H∞-Norm of a Передаточная Функция Matrix», System Control Letters, 14 (1990), pp. 287-293.
connect | genss | looptuneOptions | loopview | systune | TuningGoal.Gain | TuningGoal.LoopShape | TuningGoal.Tracking | diskmargin (Robust Control Toolbox) | hinfstruct (Robust Control Toolbox) | looptune (for slTuner) (Simulink Control Design) | slTuner (Simulink Control Design)