Чтобы создать объект IRFunctionCurve, смотрите следующие опции:
Подбор объекта IRFunctionCurve с помощью указателя на функцию
Подбор объекта IRFunctionCurve с использованием метода Нельсона-Сигеля
Подбор объекта IRFunctionCurve с использованием метода Свенссона
Подбор объекта IRFunctionCurve с использованием метода сглаживания сплайна
Использование fitFunction для создания пользовательской функции аппроксимации
Можно использовать конструктор IRFunctionCurve с MATLAB® указатель на функцию для определения кривой процентной ставки. Для получения дополнительной информации об определении указателя на функцию см. документацию Основы Программирования MATLAB.
Этот пример использует FunctionHandle аргумент со значением @(t) t.^2 для построения кривой процентной ставки:
rr = IRFunctionCurve('Zero',today,@(t) t.^2)
rr =
Properties:
FunctionHandle: @(t)t.^2
Type: 'Zero'
Settle: 733600
Compounding: 2
Basis: 0Используйте метод, fitNelsonSiegelдля модели Нельсона-Зигеля, которая соответствует эмпирической форме кривой выражения с заранее заданной функциональной формой спотовых ставок, которая является функцией времени до погашения облигаций.
Модель Нельсона-Сигеля представляет динамическую трехфакторную модель: уровень, уклон и кривизну. Однако коэффициенты Нельсона-Сигеля являются ненаблюдаемыми или латентными, что позволяет совершить ошибку измерения, и связанные загрузки имеют экономические ограничения (форвардные ставки всегда положительны, и коэффициент дисконтирования приближается к нулю с увеличением зрелости). Для получения дополнительной информации см. «Кривые доходности с нулевым купоном: техническая документация», BIS Papers, Банк международных расчетов, № 25, октябрь 2005 г.
Этот пример использует IRFunctionCurve моделирование свободной от дефолта структуры процентных ставок в Соединенном Королевстве.
Загрузите данные:
load ukdata20080430Конвертируйте ставки репо в эквивалентные нулевые купонные облигации:
RepoCouponRate = repmat(0,size(RepoRates)); RepoPrice = bndprice(RepoRates, RepoCouponRate, RepoSettle, RepoMaturity);
Агрегируйте данные:
Settle = [RepoSettle;BondSettle];
Maturity = [RepoMaturity;BondMaturity];
CleanPrice = [RepoPrice;BondCleanPrice];
CouponRate = [RepoCouponRate;BondCouponRate];
Instruments = [Settle Maturity CleanPrice CouponRate];
InstrumentPeriod = [repmat(0,6,1);repmat(2,31,1)];
CurveSettle = datenum('30-Apr-2008');The IRFunctionCurve объект предоставляет возможность подгонки кривой Нельсона-Зигеля к наблюдаемым рыночным данным с помощью fitNelsonSiegel способ. Подбор кривой выполняется вызовом функции lsqnonlin. Этот метод имеет необходимые входы Type, Settle, и матрица данных приборов.
NSModel = IRFunctionCurve.fitNelsonSiegel('Zero',CurveSettle,... Instruments,'Compounding',-1,'InstrumentPeriod',InstrumentPeriod);
Постройте график кривой процентной ставки Нельсона-Сигела для форвардных ставок:
PlottingDates = CurveSettle+20:30:CurveSettle+365*25;
TimeToMaturity = yearfrac(CurveSettle,PlottingDates);
NSForwardRates = getForwardRates(NSModel, PlottingDates);
plot(TimeToMaturity,NSForwardRates)
title('Nelson Siegel model of UK instantaneous nominal forward curve')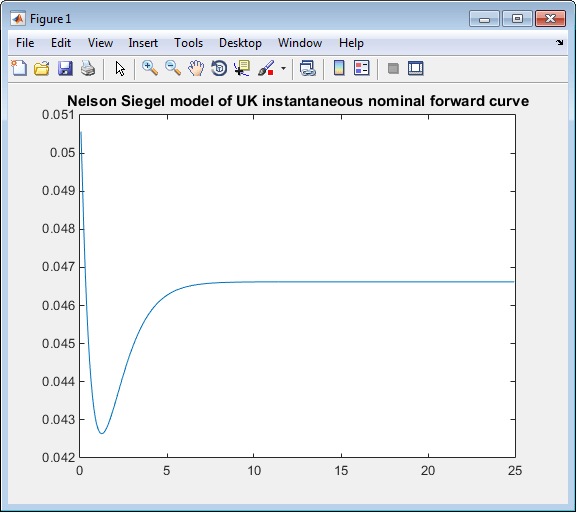
Используйте метод, fitSvenssonдля модели Свенссона, чтобы улучшить гибкость кривых и подгонку для модели Нельсона-Зигеля. В 1994 году Свенссон продлил функции Нельсона и Сигела, добавив ещё один термин, который позволяет второй «горб». Дополнительная точность достигается за счет добавления еще двух параметров, β3 и τ2, которые необходимо оценить.
В этом примере использования fitSvensson метод, IRFitOptions структура, ранее заданная с помощью IRFitOptions конструктор, используется. Таким образом, вы должны задать FitType, InitialGuess, UpperBound, LowerBound, и OptOptions параметры оптимизации для lsqnonlin.
Загрузите данные:
load ukdata20080430Конвертируйте ставки репо в эквивалентные нулевые купонные облигации:
RepoCouponRate = repmat(0,size(RepoRates)); RepoPrice = bndprice(RepoRates, RepoCouponRate, RepoSettle, RepoMaturity);
Агрегируйте данные:
Settle = [RepoSettle;BondSettle];
Maturity = [RepoMaturity;BondMaturity];
CleanPrice = [RepoPrice;BondCleanPrice];
CouponRate = [RepoCouponRate;BondCouponRate];
Instruments = [Settle Maturity CleanPrice CouponRate];
InstrumentPeriod = [repmat(0,6,1);repmat(2,31,1)];
CurveSettle = datenum('30-Apr-2008');
Определите OptOptions для IRFitOptions конструктор:
OptOptions = optimoptions('lsqnonlin','MaxFunEvals',1000); fIRFitOptions = IRFitOptions([5.82 -2.55 -.87 0.45 3.9 0.44],... 'FitType','durationweightedprice','OptOptions',OptOptions,... 'LowerBound',[0 -Inf -Inf -Inf 0 0],'UpperBound',[Inf Inf Inf Inf Inf Inf]);
Подгонка кривой процентной ставки с помощью модели Свенссона:
SvenssonModel = IRFunctionCurve.fitSvensson('Zero',CurveSettle,... Instruments,'IRFitOptions', fIRFitOptions, 'Compounding',-1,... 'InstrumentPeriod',InstrumentPeriod)
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the default value of the function tolerance. SvenssonModel = Type: Zero Settle: 733528 (30-Apr-2008) Compounding: -1 Basis: 0 (actual/actual)
Сообщение о состоянии, вывод из lsqnonlin, указывает, что оптимизация для поиска параметров уравнения Свенссона успешно завершена.
Постройте график кривой процентной ставки Свенссона для форвардных ставок:
PlottingDates = CurveSettle+20:30:CurveSettle+365*25;
TimeToMaturity = yearfrac(CurveSettle,PlottingDates);
SvenssonForwardRates = getForwardRates(SvenssonModel, PlottingDates);
plot(TimeToMaturity,SvenssonForwardRates)
title('Svensson model of UK instantaneous nominal forward curve')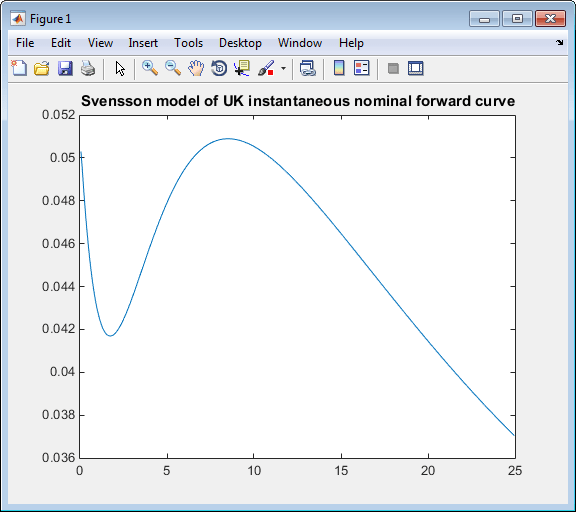
Используйте метод, fitSmoothingSpline, чтобы смоделировать структуру термина с помощью сплайна, в частности, структура термина представляет собой прямую кривую с кубическим сплайном.
Примечание
Для использования Toolbox™ необходимо иметь лицензию на программное обеспечение Curve Fitting fitSmoothingSpline способ.
The IRFunctionCurve объект используется для аппроксимации сглаживающего сплайна передней кривой с функцией штрафа. Требуемые входы Type, Settle, матрица Instruments, и Lambdafun, указатель на функцию, содержащий штрафную функцию
Загрузите данные:
load ukdata20080430Конвертируйте ставки репо в эквивалентные нулевые купонные облигации:
RepoCouponRate = repmat(0,size(RepoRates)); RepoPrice = bndprice(RepoRates, RepoCouponRate, RepoSettle, RepoMaturity);
Агрегируйте данные:
Settle = [RepoSettle;BondSettle];
Maturity = [RepoMaturity;BondMaturity];
CleanPrice = [RepoPrice;BondCleanPrice];
CouponRate = [RepoCouponRate;BondCouponRate];
Instruments = [Settle Maturity CleanPrice CouponRate];
InstrumentPeriod = [repmat(0,6,1);repmat(2,31,1)];
CurveSettle = datenum('30-Apr-2008');
Выберите параметры для Lambdafun:
L = 9.2; S = -1; mu = 1;
Определите Lambdafun функция штрафа:
lambdafun = @(t) exp(L - (L-S)*exp(-t/mu)); t = 0:.1:25; y = lambdafun(t); figure semilogy(t,y); title('Penalty Function for VRP Approach') ylabel('Penalty') xlabel('Time')
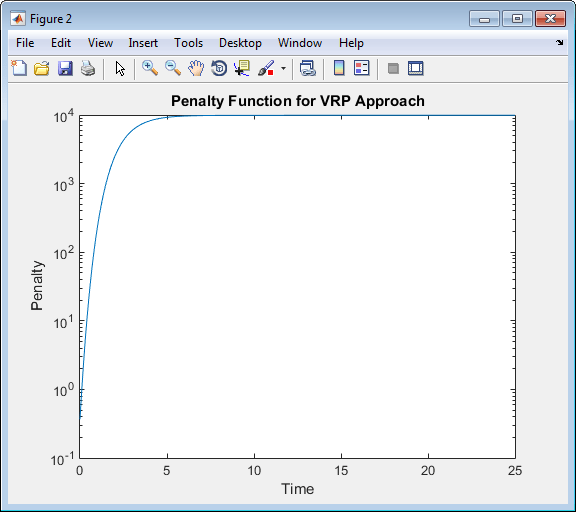
Используйте fitSmoothinSpline метод для подгонки кривой процентной ставки и моделирования Lambdafun функция штрафа:
VRPModel = IRFunctionCurve.fitSmoothingSpline('Forward',CurveSettle,... Instruments,lambdafun,'Compounding',-1, 'InstrumentPeriod',InstrumentPeriod);
Постройте график сглаживания кривой процентной ставки сплайна для форвардных ставок:
PlottingDates = CurveSettle+20:30:CurveSettle+365*25;
TimeToMaturity = yearfrac(CurveSettle,PlottingDates);
VRPForwardRates = getForwardRates(VRPModel, PlottingDates);
plot(TimeToMaturity,VRPForwardRates)
title('Smoothing Spline model of UK instantaneous nominal forward curve')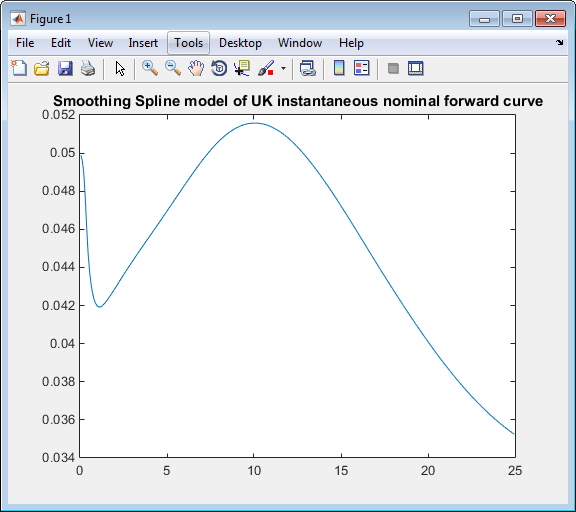
При использовании IRFunctionCurve объект, можно создать пользовательскую функцию аппроксимации с fitFunction способ. Как использовать fitFunction, вы должны задать FunctionHandle. В сложение необходимо также использовать конструктор IRFitOptions для определения IRFitOptionsObj для поддержки InitialGuess для параметров функции кривой.
Следующий пример демонстрирует использование fitFunction с FunctionHandle и IRFitOptionsObj:
Settle = repmat(datenum('30-Apr-2008'),[6 1]); Maturity = [datenum('07-Mar-2009');datenum('07-Mar-2011');... datenum('07-Mar-2013');datenum('07-Sep-2016');... datenum('07-Mar-2025');datenum('07-Mar-2036')]; CleanPrice = [100.1;100.1;100.8;96.6;103.3;96.3]; CouponRate = [0.0400;0.0425;0.0450;0.0400;0.0500;0.0425]; Instruments = [Settle Maturity CleanPrice CouponRate]; CurveSettle = datenum('30-Apr-2008');
Определите FunctionHandle:
functionHandle = @(t,theta) polyval(theta,t);
Определите OptOptions для IRFitOptions:
OptOptions = optimoptions('lsqnonlin','display','iter');
Определите fitFunction:
CustomModel = IRFunctionCurve.fitFunction('Zero', CurveSettle, ... functionHandle,Instruments, IRFitOptions([.05 .05 .05],'FitType','price',... 'OptOptions',OptOptions));
Norm of First-order
Iteration Func-count f(x) step optimality CG-iterations
0 4 38036.7 4.92e+04
1 8 38036.7 10 4.92e+04 0
2 12 38036.7 2.5 4.92e+04 0
3 16 38036.7 0.625 4.92e+04 0
4 20 38036.7 0.15625 4.92e+04 0
5 24 30741.5 0.0390625 1.72e+05 0
6 28 30741.5 0.078125 1.72e+05 0
7 32 30741.5 0.0195312 1.72e+05 0
8 36 28713.6 0.00488281 2.33e+05 0
9 40 20323.3 0.00976562 9.47e+05 0
10 44 20323.3 0.0195312 9.47e+05 0
11 48 20323.3 0.00488281 9.47e+05 0
12 52 20323.3 0.0012207 9.47e+05 0
13 56 19698.8 0.000305176 1.08e+06 0
14 60 17493 0.000610352 7e+06 0
15 64 17493 0.0012207 7e+06 0
16 68 17493 0.000305176 7e+06 0
17 72 15455.1 7.62939e-05 2.25e+07 0
18 76 15455.1 0.000177499 2.25e+07 0
19 80 13317.1 3.8147e-05 3.18e+07 0
20 84 12865.3 7.62939e-05 7.83e+07 0
21 88 11779.8 7.62939e-05 7.58e+06 0
22 92 11747.6 0.000152588 1.45e+05 0
23 96 11720.9 0.000305176 2.33e+05 0
24 100 11667.2 0.000610352 1.48e+05 0
25 104 11558.6 0.0012207 3.55e+05 0
26 108 11335.5 0.00244141 1.57e+05 0
27 112 10863.8 0.00488281 6.36e+05 0
28 116 9797.14 0.00976562 2.53e+05 0
29 120 6882.83 0.0195312 9.18e+05 0
30 124 6882.83 0.0373993 9.18e+05 0
31 128 3218.45 0.00934981 1.96e+06 0
32 132 612.703 0.0186996 3.01e+06 0
33 136 13.0998 0.0253882 3.05e+06 0
34 140 0.0762922 0.00154002 5.05e+04 0
35 144 0.0731652 3.61102e-06 29.9 0
36 148 0.0731652 6.32335e-08 0.063 0
Local minimum possible.
lsqnonlin stopped because the final change in the sum of squares relative to
its initial value is less than the default value of the function tolerance.
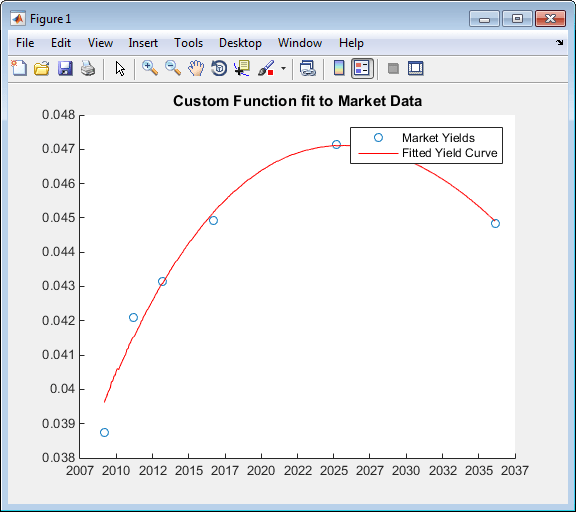
Постройте график пользовательской функции, которая определяется с помощью fitFunction:
Yields = bndyield(CleanPrice,CouponRate,Settle(1),Maturity); scatter(Maturity,Yields); PlottingPoints = min(Maturity):30:max(Maturity); hold on; plot(PlottingPoints, getParYields(CustomModel, PlottingPoints),'r'); datetick legend('Market Yields','Fitted Yield Curve') title('Custom Function fit to Market Data')
IRBootstrapOptions | IRDataCurve | IRFitOptions | IRFunctionCurve