Прогнозирование кредитных потерь для контрагента зависит от трех основных элементов:
Вероятность дефолта (PD)
Экспозиция по умолчанию (EAD), значение инструмента в какое-то будущее время
Потеря по умолчанию (LGD), которое определяется как 1 − Recovery
Если эти величины известны в будущие t времени, ожидаемые потери PD × EAD × LGD. В этом случае можно смоделировать ожидаемый убыток для одного контрагента с помощью биномиального распределения. Сложность возникает, когда вы моделируете портфель этих контрагентов, и вы хотите симулировать их с некоторой корреляцией по умолчанию.
Чтобы симулировать коррелированные значения по умолчанию, модель копула связывает каждый контрагент со случайной переменной, называемой «скрытой» переменной. Эти скрытые переменные коррелируются с помощью некоторого прокси для их кредитоспособности, например, их цена акций. Эти скрытые переменные затем сопоставляются с результатами по умолчанию или не по умолчанию, так что значение по умолчанию происходит с вероятностью PD.
Этот рисунок суммирует подход симуляции копулы.
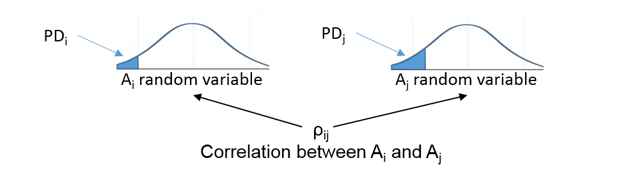
Случайная переменная A i, сопоставленная с i-м контрагентом, с вероятностью попадает в заштрихованную область по умолчанию PDi. Если моделируемое значение падает в этой области, оно интерпретируется как значение по умолчанию. j-й контрагент следует аналогичному шаблону. Если A i и A j случайных переменных сильно коррелируют, они оба, как правило, имеют высокие значения (нет по умолчанию) или оба имеют низкие значения (падение в области по умолчанию). Поэтому существует корреляция по умолчанию.
Для эмитентов M необходимы M (M − 1 )/2 параметров корреляции. Для M = 1000 это около полумиллиона корреляций. Одним из практических изменений подхода является однофакторная модель, которая делает все скрытые переменные зависимыми от одного фактора. Этот фактор Z представляет собой базовое системное качество кредита в экономике. Эта модель также включает случайную идиосинкратическую ошибку.
Это значительно снижает требования к входным данным, потому что теперь нужны только M чувствительности, то есть веса w1, …, wM. Если Z и i являются стандартными нормальными переменными, то A i также является стандартным нормальным.
Расширение однофакторной модели является многофакторной моделью.
Эта модель имеет несколько факторов, каждый из которых связан с некоторым базовым драйвером кредита. Для примера можно иметь факторы для разных областей или стран, или для разных отраслей. Каждая латентная переменная теперь является комбинацией нескольких случайных переменных плюс идиосинкратическая ошибка (эпсилон) снова.
Когда латентные переменные A i обычно распределены, существует Гауссова копула. Общая альтернатива состоит в том, чтобы позволить латентным переменным следовать t распределению, которое приводит к t копуле. t копулы приводят к более тяжелым хвостам, чем гауссовы копулы. Подразумеваемая кредитная корреляция также больше с t копулами. Переключение между этими двумя подходами к копуле может предоставить важную информацию о рисках модели.
Risk Management Toolbox™ поддерживает симуляции дефолтов по кредитам контрагентов и миграций кредитного рейтинга контрагентов.
The creditDefaultCopula объект используется для моделирования и анализа мультифакторных симуляций кредитного дефолта. Эти симуляции предполагают, что вы вычисляли основные входы этой модели самостоятельно. Основными входами для этой модели являются:
PD - Вероятность дефолта
EAD - Воздействие по умолчанию
LGD - Потеря по умолчанию (1 − Recovery)
Weights - Коэффициент и идиосинкратичные веса
FactorCorrelation - Необязательная матрица факторной корреляции для многофакторных моделей
The creditDefaultCopula объект позволяет моделировать значения по умолчанию с помощью многофакторной копулы и возвращать результаты как распределение потерь на уровне портфеля и контрагента. Можно также использовать creditDefaultCopula Целью является расчет нескольких мер риска на уровне портфеля и взносов на риск от отдельных должников. Выходные выходы creditDefaultCopula модель и связанные с ней функции:
Полное моделируемое распределение потерь портфеля по сценариям и потерь по каждому контрагенту по сценариям. Для получения дополнительной информации смотрите creditDefaultCopula свойства объекта и simulate.
Меры риска (VaR, CVaR, EL, Std) с доверительными интервалами. Посмотрите portfolioRisk.
Взносы в риск на контрагента (для EL и CVaR). Посмотрите riskContribution.
Меры риска и связанные доверием диапазоны. Посмотрите confidenceBands.
Подробные данные сценария контрагента для индивидуальных потерь для каждого контрагента. Посмотрите getScenarios.
The creditMigrationCopula позволяет моделировать изменения в кредитном рейтинге для каждого контрагента.
The creditMigrationCopula объект используется для моделирования миграции контрагентского кредита. Эти симуляции предполагают, что вы вычисляли основные входы этой модели самостоятельно. Основными входами для этой модели являются:
migrationValues - Значения позиций контрагента для каждого кредитного рейтинга.
ratings - Текущий кредитный рейтинг для каждого контрагента.
transitionMatrix - Матрица вероятностей перехода кредитного рейтинга.
LGD - Потеря по умолчанию (1 − Recovery)
Weights - Коэффициентные и идиосинкратические веса модели
Можно также использовать creditMigrationCopula Целью является расчет нескольких мер риска на уровне портфеля и взносов на риск от отдельных должников. Выходные выходы creditMigrationCopula модель и связанные с ней функции:
Полное моделируемое распределение значений портфеля. Для получения дополнительной информации смотрите creditMigrationCopula свойства объекта и simulate.
Меры риска (VaR, CVaR, EL, Std) с доверительными интервалами. Посмотрите portfolioRisk.
Взносы в риск на контрагента (для EL и CVaR). Посмотрите riskContribution.
Меры риска и связанные доверием диапазоны. Посмотрите confidenceBands.
Подробные данные сценария контрагента для каждого контрагента. Посмотрите getScenarios.
asrf | creditDefaultCopula | creditMigrationCopula