erfcДополнительная функция ошибок
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
erfc(x) erfc(x,n)
вычисляет дополнительную функцию ошибок.
с erfc(x, 0) = erfc(x) и возвращает повторные интегралы дополнительной функции ошибок. Вызовы erfc(x) и erfc(x, 0) эквивалентны.
erfc задан для всех сложных аргументов x. Для аргументов с плавающей точкой, erfc возвращает результаты с плавающей точкой.
Реализованные точные значения:
erfc(0) = 1, erfc(∞) = 0, erfc(-∞) = 2, erfc(i∞) = 1 - i∞, erfc(-i∞) = 1 + i∞
, erfc(∞,n) = 0, erfc(-∞, n) = ∞
Для всех других аргументов функция ошибок возвращает символьные вызовы функции.
Если численное значение n не целое число или если n < -1, вызов функции erfc(x, n) возвращает ошибку. Функция также принимает символьные значения n.
Если n численное значение, можно использовать expand(erfc(x, n)) применять следующие правила. Смотрите Пример 3.
Повторение
Отражательное правило , где H(n,ix) n- Многочлен Эрмита степени th в точке ix. Смотрите orthpoly::hermite.
Для функционального erfc с аргументами с плавающей точкой большого абсолютного значения могут произойти внутренняя числовая потеря значимости или переполнение. Смотрите Пример 2. Если вызов erfc потеря значимости причин или переполнение, эта функция возвращается:
Результат, усеченный к 0.0 если x большое положительное вещественное число
Результат округлен к 2.0 если x большое отрицательное вещественное число
RD_NAN если x большое комплексное число, и MuPAD® не может аппроксимировать значение функции
MuPAD может упростить выражения, которые содержат функции ошибок и их инверсии. Для действительных значений x, система применяет следующие правила упрощения:
inverf(erf(x)) = inverf(1 - erfc(x)) = inverfc(1 - erf(x)) = inverfc(erfc(x)) = x
inverf(-erf(x)) = inverf(erfc(x) - 1) = inverfc(1 + erf(x)) = inverfc(2 - erfc(x)) = -x
Для любого значения x, система применяет следующие правила упрощения:
inverf(-x) = -inverf(x)
inverfc(2 - x) = -inverfc(x)
erf(inverf(x)) = erfc(inverfc(x)) = x
erf(inverfc(x)) = erfc(inverf(x)) = 1 - x
Когда названо аргументом с плавающей точкой, функции чувствительны к переменной окружения DIGITS, который определяет числовую рабочую точность.
Можно вызвать дополнительную функцию ошибок с точными и символьными аргументами:
erfc(0), erfc(x + 1), erfc(-infinity), erfc(3/2), erfc(sqrt(2))
![]()
erfc(0, n), erfc(x + 1, -1), erfc(-infinity, 5)
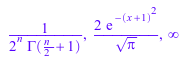
Чтобы аппроксимировать точные результаты числами с плавающей запятой, используйте float:
float(erfc(3/2)), float(erfc(sqrt(2)))
![]()
В качестве альтернативы используйте значение плавающих точек в качестве аргументов:
erfc(-7.2), erfc(2.0 + 3.5*I), erfc(3.0, 4)
![]()
Для больших сложных аргументов может возвратиться дополнительная функция ошибок![]() :
:
erfc(38000.0 + 3801.0*I)
![]()
Для больших аргументов с плавающей точкой с положительными действительными частями, erfc могут возвращаемые значения, усеченные к 0.0:
erfc(27281.1), erfc(27281.2)
![]()
diff, float, limitрасширение, rewrite, series, и другие функции обрабатывают выражения, включающие дополнительную функцию ошибок:
diff(erfc(x, 3), x, x)
![]()
limit(x/(1 + x)*(1 - erfc(x)), x = infinity)
![]()
expand(erfc(x, 3))
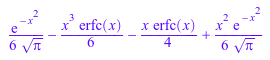
rewrite(erfc(x), erf), rewrite(erfc(x), erfi)
![]()
series(erfc(x), x = infinity, 3)
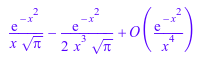
| |
|
Арифметическое выражение, представляющее целое число, больше, чем или равный |
Арифметическое выражение
erferfc, и erfi целые функции.