Фазовая модуляция

Фазовая модуляция - это метод линейной модуляции основной полосы частот, в котором сообщение модулирует фазу сигнала постоянной амплитуды. Toolbox™ связи обеспечивает модуляторы и демодуляторы для этих методов фазовой модуляции:

Фазовая манипуляция (PSK) - двоичная, квадратурная и общая PSK
Дифференциальная фазовая манипуляция (DPSK) - двоичная, квадратурная и общая DPSK
Смещение QPSK (OQPSK)

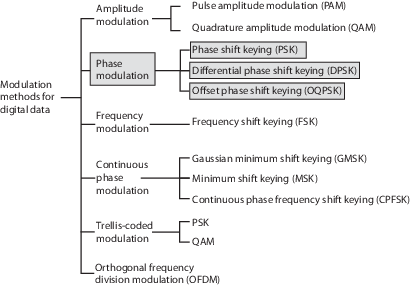
Для модуляции входных данных с помощью этих методов можно использовать функции MATLAB ®, системные объекты или блоки ^Simulink ®.

Схема модуляции	Функции MATLAB	Системные объекты	Блоки симулятора
Двоичный PSK (BPSK)		`comm.BPSKModulator` `comm.BPSKDemodulator`	Базовая полоса модулятора BPSK Базовая полоса демодулятора BPSK
Квадратурный PSK (QPSK)		`comm.QPSKModulator` `comm.QPSKDemodulator`	Основная полоса частот модулятора QPSK Базовая полоса демодулятора QPSK
Общие ПСК	`pskmod` `pskdemod`	`comm.PSKModulator` `comm.PSKDemodulator`	M-PSK модулятор основной полосы частот Базовая полоса демодулятора M-PSK
Дифференциальный BPSK (DBPSK)		`comm.DBPSKModulator` `comm.DBPSKDemodulator`	Модулятор DBPSK, основная полоса частот Базовая полоса демодулятора DBPSK
Дифференциальный QPSK (DQPSK)		`comm.DQPSKModulator` `comm.DQPSKDemodulator`	Базовая полоса модулятора DQPSK Базовая полоса демодулятора DQPSK
Общий DPSK	`dpskmod` `dpskdemod`	`comm.DPSKModulator` `comm.DPSKDemodulator`	M-DPSK модулятор основной полосы частот М-ДПСК демодулятор основной полосы частот
OQPSK		`comm.OQPSKModulator` `comm.OQPSKDemodulator`	Базовая полоса модулятора OQPSK Базовая полоса демодулятора OQPSK

Моделирование полосы частот и полосы пропускания

Communications Toolbox поддерживает методы моделирования полосы частот и полосы пропускания; однако методы фазовой манипуляции поддерживают только моделирование основной полосы частот.

Общая форма сигнала полосы пропускания может быть представлена как

$_{Y1} (t) cos (_{} 2.dfct +_{}_{}$

где _ФК - несущая частота, и θ - начальная фаза сигнала перевозчика. Это уравнение равно действительной части

$[(_{Y1} (t) +_{} jY2 (^{t)}) ej_{}$

При моделировании основной полосы моделируется только выражение в квадратных скобках. Вектор y является выборкой комплексного сигнала

$(_{Y1} (t) +_{} jY2 (^{t}$ ))

BPSK

При двоичной фазовой манипуляции (BPSK) фаза сигнала постоянной амплитуды переключается между двумя значениями, соответствующими двоичному 1 и двоичному 0. Форма сигнала полосы пропускания сигнала BPSK равна

$_{sn} (t) \sqrt{\frac{=_{}}{_{}}} 2EbTbcos_{(}_{} 2.dfct$ + δ n),

где:

_Eb - энергия на бит.
_Tb - длительность бита.
_fc - несущая частота.

В MATLAB представление основной полосы сигнала BPSK равно

$_{sn} (t)^{= e_{}} - iü n =$ cos (øn).

Сигнал BPSK имеет две фазы: 0 и δ.

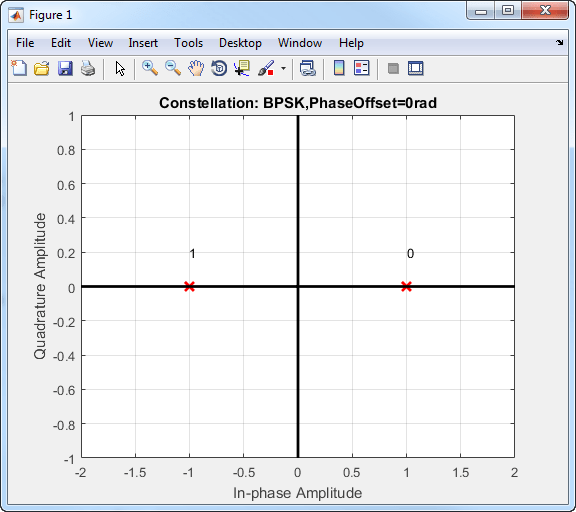
Вероятность битовой ошибки в канале AWGN равна

$_{Pb} = \sqrt{\frac{Q_{(}}{_{}}}$ 2EbN0),

где _N0 - спектральная плотность мощности шума.

QPSK

При квадратурной фазовой манипуляции биты сообщения группируются в 2-битовые символы, которые передаются как одна из четырех фаз сигнала основной полосы постоянной амплитуды. Эта группировка обеспечивает эффективность полосы пропускания, которая в два раза превышает эффективность BPSK. Общий сигнал QPSK выражается как

$_{sn} (t) \sqrt{\frac{=_{}}{_{}}} 2EsTscos_{(} 2.dfct + \frac{(}{} 2n + 1) ¼ 4);$ n∈{0,1,2,3},

где _Es - энергия на символ, а _Ts - длительность символа. Комплексное представление основной полосы сигнала QPSK

$_{sn} (t) = \exp \frac{(jδ}{(} 2n + 14));$ n∈{0,1,2,3}.

На этой диаграмме совокупности QPSK каждая 2-битовая последовательность отображается в одно из четырех возможных состояний. Состояния соответствуют фазам δ/4, 3λ/4, 5λ/4 и 7λ/4.

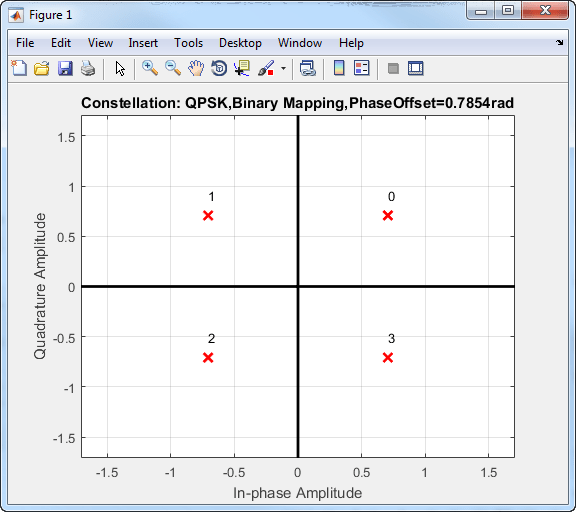
Чтобы улучшить эффективность частоты битовых ошибок, входящие биты могут быть отображены в последовательность, кодированную Серым.

Отображение двоичного в серый

Двоичная последовательность	Последовательность с серым кодом
00	00
01	01
10	11
11	10

Основное преимущество кода Грея заключается в том, что только один из двух битов изменяется при перемещении между соседними точками созвездия. Серые коды могут быть применены к модуляциям более высокого порядка, как показано в этой группе QPSK с серым кодом.

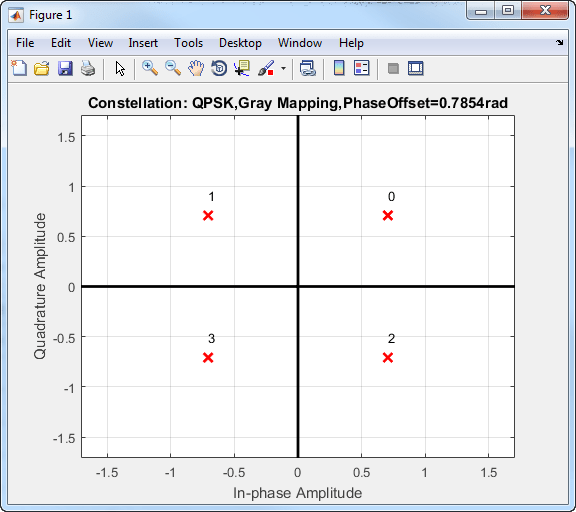
Вероятность битовых ошибок для QPSK в AWGN с серым кодированием равна

$_{Pb} = \sqrt{\frac{Q_{(}}{_{}}}$ 2EbN0),

которое совпадает с выражением для BPSK. В результате QPSK обеспечивает одинаковую производительность с удвоенной эффективностью полосы пропускания.

PSK высшего порядка

В MATLAB можно модулировать и демодулировать совокупности PSK более высокого порядка. Комплексная форма основной полосы для M-ary PSK-сигнала с использованием преобразования символов с естественным двоичным порядком является

$_{sn} (t) = \exp \frac{(jδ}{(} 2n + 1M)); n\in{0,1,$ ..., M − 1}.

Это 8-PSK созвездие использует отображение символов с серым кодированием.

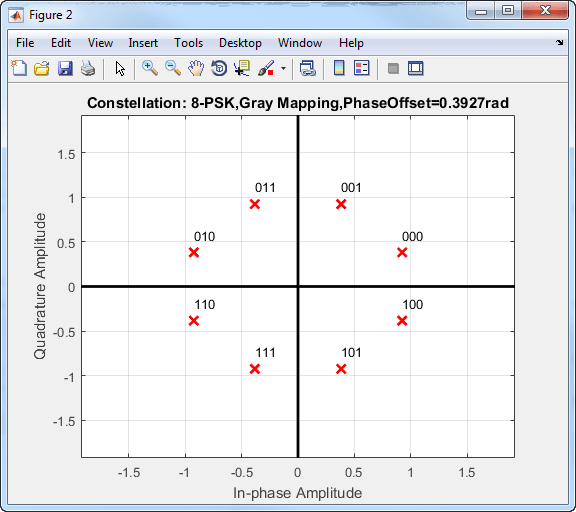
Для порядков модуляции более 4 эффективность частоты битовых ошибок PSK в AWGN ухудшается. На следующем рисунке кривые QPSK и BPSK перекрываются друг с другом.

DPSK

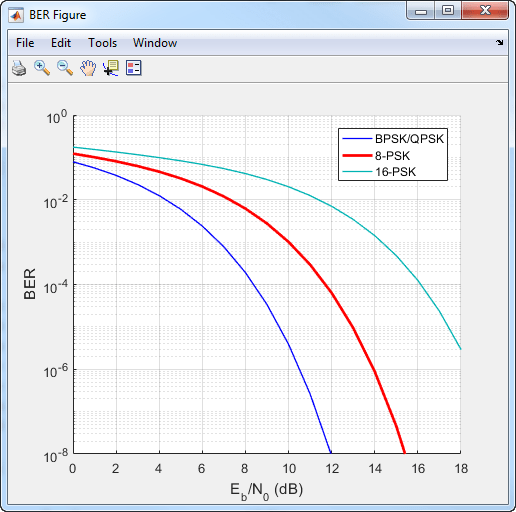
ДФМ является некогерентной формой фазовой манипуляции, которая не требует когерентного опорного сигнала в приемнике. При использовании DPSK разность между последовательными входными символами отображается в конкретную фазу. Например, для двоичного ДФМ (ДБФМ) схема модуляции работает так, что разность между последовательными битами отображается в двоичный 0 или 1. Когда входной бит равен 1, дифференциально кодированный символ остается таким же, как предыдущий символ, в то время как входящий 0 переключает выходной символ.

Недостатком ДФМ является то, что он примерно на 3 дБ менее энергоэффективен, чем когерентный ФМ. Вероятность битовых ошибок для DBPSK в AWGN равна _Pb = 1/2 exp (_Eb/N0 ).

OQPSK

Смещение QPSK аналогично QPSK, за исключением того, что выравнивание по времени синфазного и квадратурного потоков битов различается. В QPSK синфазные и квадратурные потоки битов переходят одновременно. В OQPSK переходы имеют смещение полупериода полусимвола, как показано.

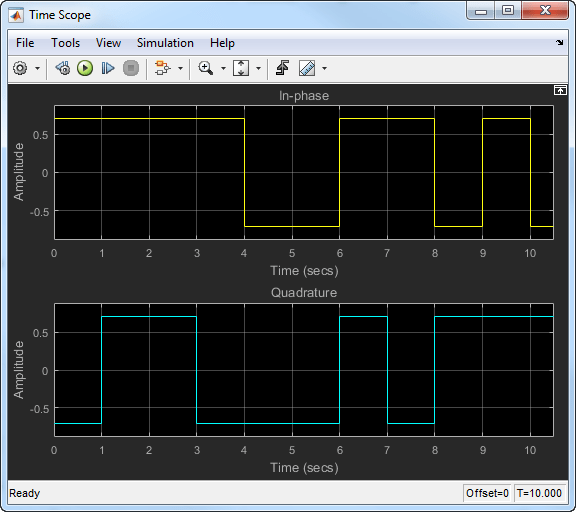
Синфазный и квадратурный сигналы переходят только по границам между символами. Эти переходы происходят с интервалом в 1 секунду, поскольку частота дискретизации составляет 1 Гц. На следующем рисунке показаны синфазные и квадратурные сигналы для сигнала OQPSK.

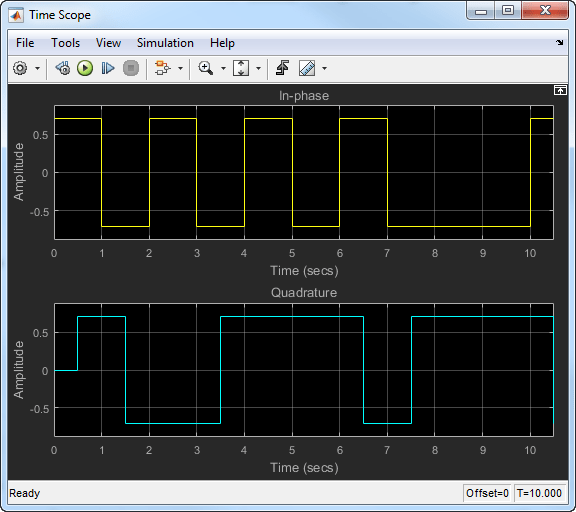
Для OQPSK квадратурный сигнал имеет смещение периода символа 1/2 (0,5 с).

BER для сигнала OQPSK в AWGN идентичен сигналу QPSK. BER:

$_{Pb} = \sqrt{\frac{Q_{(}}{_{}}}$ 2EbN0),

где _Eb - энергия на бит, а _N0 - спектральная плотность мощности шума.

Демодуляция с мягким решением

Все функции демодулятора Communications Toolbox, системные объекты и блоки могут демодулировать двоичные данные с помощью жестких или мягких решений. Доступны два алгоритма мягкого решения: точное логарифмическое отношение правдоподобия (LLR) и приблизительное LLR. Точная LLR обеспечивает наибольшую точность, но медленнее, в то время как приблизительная LLR менее точна, но более эффективна.

Точный алгоритм LLR

Логарифмическое отношение правдоподобия (LLR) является логарифмом отношения вероятностей 0-бита, передаваемого, и 1-бита, передаваемого для принимаемого сигнала. LLR для бита b определяется как:

$L (b) = \frac{\log (Pr (b = 0 |}{r = (x, y)) Pr}$ (b = 1 | r = (x, y)))

Предполагая равную вероятность для всех символов, LLR для канала AWGN может быть выражено как:

$L (b) = \frac{\underset{\log (_{}}{}^{\frac{}{^{}} {\sums\inS0e-1σ2_{(} (}^{x} {- {sx}_{)}}^{2}}}{\underset{(y_{}}{+} -^{\frac{}{{sy}^{)}} {2)_{}}^{} {_{∑s∈S1e−1σ2}}^{(} (}} x$ − sx) 2 + (y − sy) 2))

Переменная	Описание
$r$	Принятый сигнал с координатами (x, y)
$b$	Переданный бит (один из К битов в М-образном символе, предполагая, что все М символов одинаково вероятны)
$_{S0}$	Идеальные символы или точки созвездия с битом 0, в данной позиции бита
$_{S1}$	Идеальные символы или точки созвездия с битом 1, в заданном положении бита
$_{sx}$	Синфазная координата идеального символа или точки созвездия
$_{sy}$	Квадратурная координата идеального символа или точки созвездия
$^{σ2}$	Дисперсия шума сигнала основной полосы частот
$_{}^{σx2}$	Дисперсия шума вдоль синфазной оси
$_{}^{σy2}$	Дисперсия шума по квадратурной оси

Примечание

Шумовая составляющая по синфазной и квадратурной осям принимается независимой и равной мощности, то есть $_{}^{}_{}^{}^{}$

Приблизительный алгоритм LLR

Приблизительное LLR вычисляется с использованием только ближайшей точки созвездия к принятому сигналу с 0 (или 1) в этой позиции бита, а не всех точек созвездия, как сделано в точном LLR. Он определяется в [2] как:

$L (b) \frac{=}{^{−}} \underset{(_{}}{1start2} {{mins∈S0}_{} (}^{(} x − {sx)_{} 2}^{} + \underset{y -_{}}{(} {sy) 2_{)}}^{} {{−mins∈S1}_{} (}^{(} x$ − sx) 2 + (y − sy) 2))

Ссылки

[1] Раппапорт, Теодор С. Беспроводные коммуникации: принципы и практика. Река Верхнее Седло, Нью-Джерси: Прентис Холл, 1996, стр. 238-248.

[2] Витерби, А. Дж. «Интуитивное обоснование и упрощенная реализация декодера MAP для сверточных кодов», IEEE Journal on Selected Areas in Communications. Том 16, № 2, февраль 1998 года, стр. 260-264

Документация