Спецификации модели AR

Модель AR по умолчанию

В этом примере показано использование краткого текста arima(p,D,q) синтаксис для задания модели AR (p) по умолчанию ,

$_{yt} = c_{} +_{} {δ 1yt-1}_{} +_{. . .} +_{}$ δpyt-p + αt.

По умолчанию все параметры в созданном объекте модели имеют неизвестные значения, а инновационное распределение является гауссовым с постоянной дисперсией.

Укажите модель AR (2) по умолчанию :

Mdl = arima(2,0,0)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 0
        Constant: NaN
              AR: {NaN NaN} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

Выходные данные показывают, что созданный объект модели, Mdlимеет NaN значения для всех параметров модели: постоянный член, коэффициенты AR и дисперсия. Можно изменить созданный объект модели с помощью точечной нотации или ввести его (вместе с данными) в estimate.

Модель AR без постоянного термина

Открыть сценарий в реальном времени

В этом примере показано, как задать модель AR (p) с постоянным членом, равным нулю. Используйте синтаксис имя-значение, чтобы указать модель, которая отличается от модели по умолчанию .

Укажите модель AR (2) без постоянного члена,

$_{yt} =_{}_{}_{}_{}_{}$

где инновационное распределение является гауссовым с постоянной дисперсией.

Mdl = arima('ARLags',1:2,'Constant',0)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 0
        Constant: 0
              AR: {NaN NaN} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

ARLags аргумент name-value указывает задержки, соответствующие ненулевым коэффициентам AR. Собственность Constant в созданной модели объект равен 0, как уточняется. Объект модели имеет значения по умолчанию для всех других свойств, включая NaN значения в качестве местозаполнителей для неизвестных параметров: коэффициентов AR и скалярной дисперсии.

Можно изменить созданный объект модели с помощью точечной нотации или ввести его (вместе с данными) в estimate.

Модель AR с несектутивными лагами

Открыть сценарий в реальном времени

В этом примере показано, как задать модель AR (p) с ненулевыми коэффициентами при несектутивных лагах .

Укажите модель AR (4) с ненулевыми коэффициентами AR на лагах 1 и 4 (и без постоянного члена),

$_{yt} = 0,2 +_{0 .}_{}_{}$ 8yt-1-0,1 yt-4 + αt,

где инновационное распределение является гауссовым с постоянной дисперсией.

Mdl = arima('ARLags',[1,4],'Constant',0)

Mdl = 
  arima with properties:

     Description: "ARIMA(4,0,0) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 4
               D: 0
               Q: 0
        Constant: 0
              AR: {NaN NaN} at lags [1 4]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

Выходные данные показывают ненулевые коэффициенты AR на лагах 1 и 4, как указано. Собственность P равно 4, количество предварительных наблюдений, необходимых для инициализации модели AR. Неограниченные параметры равны NaN.

Отображение значения AR:

Mdl.AR

ans=1×4 cell array
    {[NaN]}    {[0]}    {[0]}    {[NaN]}

AR массив ячеек возвращает четыре элемента. Первый и последний элементы (соответствующие лагам 1 и 4) имеют значение NaN, указывая, что эти коэффициенты ненулевые и должны быть оценены или иным образом определены пользователем. arima устанавливает коэффициенты с промежуточными лагами, равными нулю, для поддержания согласованности с индексацией массива ячеек MATLAB ® .

Модель ARMA с известными значениями параметров

Открыть сценарий в реальном времени

В этом примере показано, как указать модель ARMA (p, q) с известными значениями параметров. Такую полностью заданную модель можно использовать в качестве входных данных дляsimulate или forecast.

Укажите модель ARMA (1,1)

$_{yt} = 0,3 +_{}_{} 0,7βyt-1 +_{αt +}$ 0,4αt-1,

где инновационным распределением является t Стьюдента с 8 степенями свободы и постоянной дисперсией 0,15.

tdist = struct('Name','t','DoF',8);
Mdl = arima('Constant',0.3,'AR',0.7,'MA',0.4,...
    'Distribution',tdist,'Variance',0.15)

Mdl = 
  arima with properties:

     Description: "ARIMA(1,0,1) Model (t Distribution)"
    Distribution: Name = "t", DoF = 8
               P: 1
               D: 0
               Q: 1
        Constant: 0.3
              AR: {0.7} at lag [1]
             SAR: {}
              MA: {0.4} at lag [1]
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: 0.15

Указаны все значения параметров, то есть свойство объекта отсутствует NaN-значение.

Модель AR с распределением инноваций

Открыть сценарий в реальном времени

В этом примере показано, как указать модель AR (p) с распределением инноваций Student's .

Укажите модель AR (2) без постоянного члена ,

$_{yt} =_{}_{}_{}_{}_{}$

где нововведения следуют за распределением Стьюдента с неизвестными степенями свободы.

Mdl = arima('Constant',0,'ARLags',1:2,'Distribution','t')

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,0) Model (t Distribution)"
    Distribution: Name = "t", DoF = NaN
               P: 2
               D: 0
               Q: 0
        Constant: 0
              AR: {NaN NaN} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

Значение Distribution является struct массив с полем Name равно 't' и на местах DoF равно NaN. NaN значение указывает, что степени свободы неизвестны и должны быть оценены с помощью estimate или иным образом, указанным пользователем.

Укажите модель AR с помощью приложения Econometric Modeler

В приложении Econometric Modeler можно указать структуру запаздывания, наличие константы и инновационное распределение модели AR (p), выполнив следующие действия. Все указанные коэффициенты неизвестны и поддаются оценке.

В командной строке откройте приложение Econometric Modeler.
```
econometricModeler
```
Можно также открыть приложение из галереи приложений (см. Econometric Modeler).
На панели Временной ряд (Time Series) выберите временной ряд ответа, по которому будет соответствовать модель.
На вкладке Econometric Modeler в разделе Models щелкните AR.
Откроется диалоговое окно Параметры модели AR (AR Model Parameters).
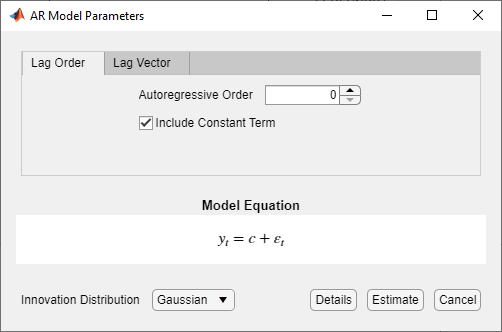
Укажите структуру запаздывания. Чтобы указать модель AR (p), которая включает все задержки AR от 1 до p, используйте вкладку Порядок задержки (Lag Order). Для обеспечения гибкости при определении включения определенных лагов используйте вкладку Вектор лага (Lag Vector). Дополнительные сведения см. в разделе Интерактивное определение многочленов оператора задержки. Независимо от используемой вкладки можно проверить форму модели, проверив уравнение в разделе «Уравнение модели».

Например:

Чтобы указать модель AR (2), которая включает константу, включает первое отставание и имеет распределение гауссовых инноваций, установите авторегрессионный порядок в2.
Чтобы указать модель AR (2), которая включает первое отставание, имеет гауссово распределение, но не включает константу:
1. Задать авторегрессионный порядок как 2.
2. Снимите флажок Включить постоянный термин (Include Constant Term).
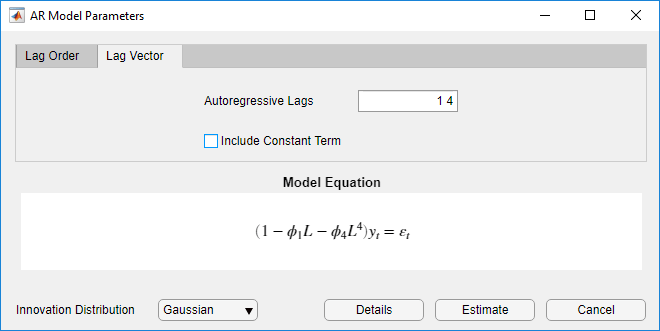
Задание модели AR (4), содержащей несектутивные задержки
$_{yt}_{}_{=ϕ1yt−1}_{}_{+ϕ4yt−4}_{+εt},$
где _αt - серия гауссовых инноваций IID:
1. Перейдите на вкладку Вектор задержки (Lag Vector).
2. Установить авторегрессионные задержки в значение 1 4.
3. Снимите флажок Включить постоянный термин (Include Constant Term).
Чтобы указать модель AR (2), которая включает первое отставание, включает постоянный член и имеет t-распределенные инновации:
1. Установить авторегрессионные задержки в значение 2.
2. Нажмите кнопку Распределение инноваций и выберите t.
Параметр степеней свободы распределения t является неизвестным, но оцениваемым параметром.

После задания модели щелкните Оценка (Estimate), чтобы оценить все неизвестные параметры в модели.

Документация