Идентификация системы - методология построения математических моделей динамических систем с использованием измерений входных и выходных сигналов системы.
Процесс идентификации системы требует от вас:
Измерьте входные и выходные сигналы системы во временной или частотной области.
Выберите структуру модели.
Применение метода оценки для оценки значений для регулируемых параметров в структуре модели-кандидате.
Оцените расчетную модель, чтобы проверить, соответствует ли модель требованиям приложения.
В динамической системе значения выходных сигналов зависят как от мгновенных значений входных сигналов, так и от прошлого поведения системы. Например, автокресло - это динамическая система - форма сиденья (положение посадки) зависит как от текущего веса пассажира (мгновенное значение), так и от того, как долго пассажир ехал в вагоне (прошлое поведение).
Модель - это математическое соотношение между входными и выходными переменными системы. Модели динамических систем обычно описываются дифференциальными или дифференциальными уравнениями, передаточными функциями, уравнениями состояния-пространства и моделями с нулевым коэффициентом усиления полюсов.
Динамические модели можно представлять как в виде непрерывного времени, так и в виде дискретного времени.
Часто используемым примером динамической модели является уравнение движения системы пружина-масса-демпфер. Как показано на следующем рисунке, масса перемещается в ответ на усилие F (t), приложенное к основанию, к которому прикреплена масса. Входом и выходом этой системы являются сила F (t) и смещение y (t) соответственно.
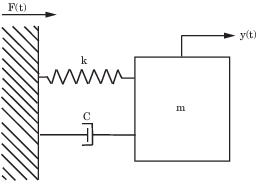
Можно представить ту же физическую систему, что и несколько эквивалентных моделей. Например, можно представить систему масса-пружина-демпфер в непрерывном времени как дифференциальное уравнение второго порядка:
= F (t)
Здесь m - масса, k - постоянная жесткости пружины, а c - коэффициент демпфирования. Решение этого дифференциального уравнения позволяет определить смещение массы y (t), как функцию внешней силы F (t) в любое время t для известных значений констант m, c и k.
Рассмотрим смещение y (t) и скорость (t) dt в качестве переменных состояния:
v (t)]
Предыдущее уравнение движения можно выразить как модель состояния-пространства системы:
t) = Cx (t)
Матрицы A, B и C связаны с константами m, c и k следующим образом:
01 м] C = [10]
Можно также получить модель передаточной функции системы пружина-масса-демпфер, взяв преобразование Лапласа дифференциального уравнения:
ms2 + cs + k)
Здесь s - переменная Лапласа.
Предположим, что можно наблюдать только входные и выходные переменные F (t) и y (t) системы масса-пружина-демпфер в дискретные моменты времени t = nTs, где Ts - фиксированный интервал времени и n = 0, 1, 2,.... Говорят, что переменные отбираются с временем Ts выборки. Затем можно представить соотношение между выборочными переменными ввода-вывода в виде уравнения разности второго порядка, например
2Ts) = bF (t − Ts)
Часто для простоты Ts принимается за одну единицу времени, и уравнение может быть записано как
2) = bF (t − 1)
Здесь a1 и a2 являются параметрами модели. Параметры модели связаны с системными константами m, c и k и временем Ts выборки.
Это уравнение разности показывает динамический характер модели. Значение смещения в момент времени t зависит не только от значения силы F в предыдущий момент времени, но также от значений смещения в предыдущие два момента времени y (t-1) и y (t-2 ).
Это уравнение можно использовать для вычисления смещения в определенное время. Смещение представляется как взвешенная сумма прошлых входных и выходных значений:
1) − a2y (t − 2)
Это уравнение показывает итеративный способ генерации значений выходного сигнала y (t), начиная с начальных условий y (0) и y (1), и измерений входного сигнала F (t). Это вычисление называется моделированием.
Альтернативно, выходное значение в данный момент времени t может быть вычислено с использованием измеренных значений выходного сигнала в предыдущие два момента времени и входного значения в предыдущий момент времени. Это вычисление называется предсказанием. Дополнительные сведения о моделировании и прогнозировании с использованием модели см. в разделах на странице Моделирование и прогнозирование.
Можно также представить дискретно-временное уравнение движения в формах state-space и transfer-function, выполнив преобразования, подобные описанным в примере динамической модели Continuous-Time.
Идентификация системы использует входные и выходные сигналы, измеряемые системой, для оценки значений регулируемых параметров в данной структуре модели. Можно создавать модели, используя входные-выходные сигналы временной области, данные частотной характеристики, сигналы временных рядов и спектры временных рядов.
Для получения хорошей модели системы необходимо иметь измеренные данные, отражающие динамическое поведение системы. Точность модели зависит от качества данных измерений, что, в свою очередь, зависит от экспериментальной конструкции.
Данные временной области состоят из входных и выходных переменных системы, которые записываются с одинаковым интервалом выборки в течение определенного периода времени.
Например, если измерить входную силу F (t) и массовое смещение y (t) системы демпфер-пружина, показанной в разделе Динамические системы и модели, при равномерной частоте дискретизации 10 Гц, будут получены следующие векторы измеренных значений:
(3Ts),..., y (NTs)]
Здесь Ts = 0,1 секунды, а NTs - время последнего измерения.
Если вы хотите построить дискретную модель из этих данных, векторы данных umeas и ymeas и время Ts выборки предоставляют достаточную информацию для создания такой модели.
Если вы хотите построить модель непрерывного времени, вы также должны знать интерсамплярное поведение входных сигналов во время эксперимента. Например, вход может быть кусочно-постоянным (удержание нулевого порядка) или кусочно-линейным (удержание первого порядка) между выборками.
Данные частотной области представляют измерения входных и выходных переменных системы, которые записываются или сохраняются в частотной области. Сигналы частотной области представляют собой преобразования Фурье соответствующих сигналов временной области.
Данные частотной области могут также представлять частотную характеристику системы, представленную набором комплексных значений отклика в заданном диапазоне частот. Частотный отклик описывает выходы на синусоидальные входы. Если входной сигнал представляет собой синусоидальную волну с частотой λ, то выходной сигнал также представляет собой синусоидальную волну с той же частотой, амплитуда которой равна А (λ), умноженной на амплитуду входного сигнала и фазовый сдвиг, равный по отношению к входному сигналу. Частотный отклик равен A (λ) e (iStart( λ)).
В случае системы масса-пружина-демпфер можно получить данные частотной характеристики, используя синусоидальную входную силу и измеряя соответствующий амплитудный коэффициент усиления и фазовый сдвиг характеристики в диапазоне входных частот.
Данные частотной области можно использовать для построения моделей системы как дискретного времени, так и непрерывного времени.
Идентификация системы требует, чтобы данные фиксировали важную динамику системы. Хорошая экспериментальная конструкция обеспечивает измерение правильных переменных с достаточной точностью и длительностью, чтобы зафиксировать динамику, которую требуется моделировать. В общем, ваш эксперимент должен:
Используйте входные данные, которые адекватно возбуждают динамику системы. Например, один шаг редко является достаточно возбуждением.
Измерьте данные достаточно долго, чтобы зафиксировать важные временные константы.
Настройте систему сбора данных, которая имеет хорошее отношение сигнал/шум.
Измерение данных с соответствующими интервалами выборки или частотным разрешением.
Перед построением модели можно проанализировать качество данных с помощью функций и методов, описанных в разделе Анализ данных. Например, можно проанализировать входные спектры, чтобы определить, имеют ли входные сигналы достаточную мощность над полосой пропускания системы. Для получения рекомендаций по анализу и обработке конкретных данных используйте advice.
С помощью инструментов непараметрического анализа на панели инструментов можно также анализировать данные для определения пиковых частот, задержек ввода, важных постоянных времени и индикации нелинейности. Эту информацию можно использовать для настройки структур модели для построения моделей на основе данных. Дополнительные сведения см. в разделе:
Структура модели - это математическая связь между входными и выходными переменными, которая содержит неизвестные параметры. Примерами структур модели являются передаточные функции с регулируемыми полюсами и нулями, уравнения состояния-пространства с неизвестными системными матрицами и нелинейные параметризованные функции.
Следующее уравнение разности представляет простую структуру модели:
= bu (k)
Здесь а и b являются регулируемыми параметрами.
Процесс идентификации системы требует выбора структуры модели и применения методов оценки для определения числовых значений параметров модели.
Для выбора структуры модели можно использовать один из следующих подходов:
Требуется модель, способная воспроизводить измеренные данные и являющаяся максимально простой. Можно попробовать различные математические структуры, доступные на панели инструментов. Такой подход к моделированию называется моделированием в черном ящике.
Для модели требуется определенная структура, которая может быть получена из первых принципов, но не знает числовых значений ее параметров. Структуру модели можно представить как набор уравнений или как систему «состояние-пространство» в MATLAB ® и оценить значения ее параметров по данным. Этот подход известен как моделирование «серого ящика».
Программное обеспечение System Identification Toolbox™ оценивает параметры модели путем минимизации погрешности между выводом модели и измеренным откликом. Выходной ymodel линейной модели задается
ymodel (t) = Гу (t)
Здесь G - передаточная функция.
Чтобы определить G, панель инструментов минимизирует разницу между выходной ymodel (t) модели и измеренной выходной ymeas (t). Критерием минимизации является взвешенная норма погрешности, v (t), где
v (t) = ymeas (t) - ymodel (t).
ymodel (t) является одним из следующих:
Смоделированный отклик (Gu (t) модели для данного входа u (t)
Прогнозируемый отклик модели для данного входного сигнала u (t) и прошлых измерений выходного сигнала (ymeas (t-1), ymeas (t-2),...)
Соответственно, ошибка v (t) называется ошибкой моделирования или ошибкой предсказания. Алгоритмы оценки регулируют параметры в структуре модели G так, чтобы норма этой ошибки была как можно меньше.
Алгоритм оценки можно настроить следующим образом:
Конфигурирование критерия минимизации для фокусировки оценки в требуемом диапазоне частот, например, для того, чтобы сделать больший акцент на более низких частотах и понизить акцент на вкладах шума более высокой частоты. Кроме того, можно настроить критерий для определения предполагаемых потребностей приложения для модели, таких как моделирование или прогнозирование.
Задание параметров оптимизации для алгоритмов итеративной оценки.
Большинство алгоритмов оценки в данном инструментарии являются итеративными. Алгоритм итеративной оценки можно настроить, указав такие опции, как метод оптимизации и максимальное количество итераций.
Дополнительные сведения о настройке алгоритма оценки см. в разделе Параметры настройки функции потери и в разделах оценки конкретных структур модели.
Моделирование в черном ящике полезно, когда вы заинтересованы в подборе данных независимо от определенной математической структуры модели. Панель инструментов предоставляет несколько линейных и нелинейных структур модели черного ящика, которые традиционно были полезны для представления динамических систем. Эти структуры модели различаются по сложности в зависимости от гибкости, необходимой для учета динамики и шума в системе. Можно выбрать одну из этих структур и вычислить ее параметры в соответствии с данными измеренного отклика.
Черное моделирование обычно представляет собой процесс проб и ошибок, в котором оцениваются параметры различных структур и сравниваются результаты. Как правило, переход к более сложным структурам начинается с простой линейной структуры модели. Можно также выбрать структуру модели, поскольку она знакома вам более хорошо или у вас есть особые потребности в приложении.
Простейшие линейные структуры черного ящика требуют наименьшего количества опций для настройки:
Передаточная функция с заданным числом полюсов и нулей
Линейная модель ARX, которая является простейшей полиномиальной моделью ввода-вывода
Модель с пространством состояний, которую можно оценить, указав количество состояний модели
Оценка некоторых из этих структур также использует алгоритмы безразличной оценки, что еще больше снижает сложность.
Структуру модели можно настроить с помощью порядка моделей. Определение порядка модели зависит от типа выбранной модели. Например, при выборе представления передаточной функции порядок модели связан с числом полюсов и нулей. Для представления state-space порядок модели соответствует количеству состояний. В некоторых случаях, например, для линейных структур модели ARX и state-space, можно оценить порядок модели на основе данных.
Если простые структуры модели не создают хороших моделей, можно выбрать более сложные структуры модели, выполнив следующие действия.
Задание более высокого порядка модели для той же линейной структуры модели. Более высокий порядок модели увеличивает гибкость модели для захвата сложных явлений. Однако излишне высокий порядок может сделать модель менее надежной.
Явное моделирование шума путем включения члена He (t), как показано в следующем уравнении.
y (t) = Gu (t) + He (t)
Здесь H моделирует аддитивное возмущение, рассматривая возмущение как выходной сигнал линейной системы, управляемой источником белого шума e (t).
Использование структуры модели, которая явно моделирует аддитивное возмущение, может помочь повысить точность измеряемого компонента G. Кроме того, такая структура модели полезна, когда основной интерес представляет использование модели для прогнозирования будущих значений отклика.
Использование другой линейной структуры модели.
См. раздел Структуры линейной модели.
Использование нелинейной структуры модели.
Нелинейные модели обладают большей гибкостью в захвате сложных явлений, чем линейные модели сходных порядков. См. раздел Нелинейные структуры модели.
В конечном итоге выбирается простейшая структура модели, обеспечивающая наилучшее соответствие измеренным данным. Дополнительные сведения см. в разделе Оценка линейных моделей с помощью быстрого запуска.
Независимо от структуры, выбранной для оценки, модель можно упростить в соответствии с требованиями приложения. Например, можно отделить измеренную динамику (G) от динамики шума (H), чтобы получить более простую модель, которая представляет только соотношение между y и u. Можно также линеаризовать нелинейную модель относительно рабочей точки.
Линейная модель часто достаточна для точного описания динамики системы, и в большинстве случаев рекомендуется сначала попытаться подогнать линейные модели. Если выходные данные линейной модели не воспроизводят надлежащим образом измеренные выходные данные, может потребоваться использовать нелинейную модель.
Можно оценить необходимость использования нелинейной структуры модели, выведя на график отклик системы на входные данные. Если отклики отличаются в зависимости от уровня ввода или знака ввода, попробуйте использовать нелинейную модель. Например, если выходной отклик на входной шаг вверх быстрее, чем отклик на шаг вниз, может потребоваться нелинейная модель.
Перед построением нелинейной модели системы, которая, как известно, является нелинейной, попробуйте преобразовать входные и выходные переменные таким образом, чтобы отношение между преобразованными переменными было линейным. Например, рассмотрим систему, которая имеет ток и напряжение в качестве входных сигналов для погружного нагревателя, и температуру нагретой жидкости в качестве выходного сигнала. Выход зависит от входов через мощность нагревателя, которая равна произведению тока и напряжения. Вместо построения нелинейной модели для этой системы с двумя входами и одним выходом можно создать новую входную переменную, взяв произведение тока и напряжения и построив линейную модель, описывающую взаимосвязь между мощностью и температурой.
Если невозможно определить преобразования переменных, которые дают линейную связь между входными и выходными переменными, можно использовать нелинейные структуры, такие как нелинейные модели ARX или Hammerstein-Wiener. Список поддерживаемых нелинейных структур модели и сведения о том, когда их использовать, см. в разделе Нелинейные структуры модели.
Для оценки линейных и нелинейных моделей различных структур можно использовать приложение или команды System Identification. В большинстве случаев необходимо выбрать структуру модели и оценить параметры модели с помощью одной команды.
Рассмотрим систему масса-пружина-демпфер, описанную в разделе Динамические системы и модели. Если уравнение движения этой системы не известно, для построения модели можно использовать метод моделирования «черный ящик». Например, можно оценить передаточные функции или модели состояния-пространства, указав порядки этих структур модели.
Передаточная функция - отношение многочленов:
f1s + f2s2 +...)
Для системы демпфера масс-пружин эта передаточная функция
cs + k)
которая представляет собой систему без нулей и 2 полюсов.
За дискретное время передаточная функция системы масса-пружина-демпфер может быть
f1z − 1 + f2z − 2)
где порядки модели соответствуют количеству коэффициентов числителя и знаменателя (nb = 1 и nf = 2) и задержка ввода-вывода равна самой низкой степени z-1 в числителе (nk = 1).
За непрерывное время можно построить модель линейной передаточной функции с помощью tfest команда.
m = tfest(data,2,0)
Здесь, data - измеренные данные ввода-вывода, представленные в виде iddata объект, а порядок модели - это набор из числа полюсов (2) и числа нулей (0).
Аналогично, можно построить структуру выходных ошибок модели дискретного времени, используя oe команда.
m = oe(data,[1 2 1])
Порядок моделей составляет [nb nf nk] = [1 2 1]. Обычно вы не знаете заказов модели заранее. Попробуйте несколько значений заказа модели, пока не найдете заказы, которые создают приемлемую модель.
Можно также выбрать структуру «состояние-пространство» для представления системы «масса-пружина-демпфер» и оценки параметров модели с помощью ssest или n4sid команда.
m = ssest(data,2)
Вот, второй аргумент 2 представляет порядок или количество состояний в модели.
При моделировании в черном ящике не нужно уравнение движения для системы - только догадка о порядках моделей.
Дополнительные сведения о построении моделей см. в разделе Шаги по использованию приложения идентификации системы и команд оценки модели.
В некоторых ситуациях структуру модели можно вывести из физических принципов. Например, математическая зависимость между входным усилием и результирующим смещением массы в пружинно-массово-демпферной системе, показанная в разделе Динамические системы и модели, хорошо известна. В форме state-space модель задается
t) = Cx (t)
где x(t) = [y(t);v(t)] - вектор состояния. Коэффициенты A, B и C являются функциями параметров модели:
A = [0 1; -k/m -c/m]
B = [0; 1/м]
C = [1 0]
Здесь вы полностью знаете структуру модели, но не знаете значения ее параметров - m, c и k.
В подходе «серый ящик» данные используются для оценки значений неизвестных параметров структуры модели. Структура модели задается набором дифференциальных или дифференциальных уравнений в MATLAB и предоставляет некоторые начальные предположения для указанных неизвестных параметров.
Как правило, модели «серых ящиков» создаются следующим образом:
Создание структуры модели шаблона.
Конфигурирование параметров модели с начальными значениями и ограничениями (если таковые имеются).
Применение метода оценки к структуре модели и вычисление значений параметров модели.
В следующей таблице представлены способы задания структуры модели «серый ящик».
| Представление структуры «серый ящик» | Подробнее |
|---|---|
Представление структуры модели «состояние-пространство» как структурированной Можно вычислить значения параметров, такие как m, c и k, из матриц A и B. Например, m = 1/B (2) и k = -A (2,1) m. | |
Представление структуры модели «состояние-пространство» как idgrey объект модели. Можно непосредственно оценить значения параметров m, c и k. | Оценка модели «серый ящик» |
После оценки модели можно оценить качество модели следующим образом:
В конечном итоге необходимо оценить качество модели на основе того, соответствует ли модель требованиям приложения. Сведения о других доступных методах анализа модели см. в разделе Анализ модели.
Если удовлетворительная модель не получена, можно итеративно улучшить результаты, попробовав другую структуру модели, изменив настройки алгоритма оценки или выполнив дополнительную обработку данных. Если эти изменения не улучшат результаты, может потребоваться пересмотреть экспериментальную конструкцию и процедуры сбора данных.
Обычно качество модели оценивается путем сравнения отклика модели с измеренным выходным сигналом для одного и того же входного сигнала.
Предположим, что для создания динамических моделей пружинно-массовой демпферной системы используется метод моделирования черного ящика. Можно попробовать различные структуры модели и заказы, например:
model1 = arx(data, [2 1 1]); model2 = n4sid(data, 3)
Можно смоделировать эти модели с определенным вводом и сравнить их отклики с измеренными значениями смещения для того же ввода, что и для реальной системы. На следующем рисунке сравниваются смоделированные и измеренные отклики для ввода шага.
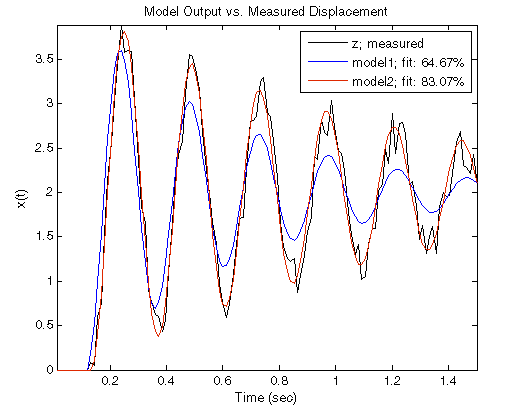
Рисунок показывает, что model2 лучше, чем model1 потому что model2 лучше подходит для данных (65% против 83%).
Процент аппроксимации указывает на соответствие между откликом модели и измеренным выходом: 100 означает идеальную аппроксимацию, а 0 - плохую аппроксимацию (то есть выход модели имеет такую же аппроксимацию к измеренному выходу, как и среднее значение измеренного выхода).
Дополнительные сведения см. в разделах на странице Сравнить выходные данные с измеренными данными (Compare Output with Measured Data).
Программа System Identification Toolbox позволяет выполнять остаточный анализ для оценки качества модели. Остатки представляют часть выходных данных, не объясненных расчетной моделью. Хорошая модель имеет остатки, не связанные с прошлыми входами.
Дополнительные сведения см. в разделах на странице Остаточный анализ.
При оценке параметров модели на основе данных получаются их номинальные значения, которые являются точными в доверительной области. Размер этой области определяется значениями неопределенностей параметров, вычисленных во время оценки. Величина неопределенностей является показателем надежности модели. Большие неопределенности в параметрах могут быть результатом излишне высокого порядка моделей, неадекватных уровней возбуждения во входных данных и плохого отношения сигнал/шум в измеренных данных.
Можно вычислить и визуализировать влияние неопределенностей параметров на отклик модели во временной и частотной областях, используя карты полюсов и нулей, графики реакции Боде и графики ступенчатой реакции. Например, на следующем графике Боде оцененной модели затененные области представляют неопределенность по амплитуде и фазе частотной характеристики модели, вычисленную с использованием неопределенности в параметрах. График показывает, что неопределенность низкая только в диапазоне частот от 5 до 50 рад/с, что указывает на то, что модель надежна только в этом диапазоне частот.
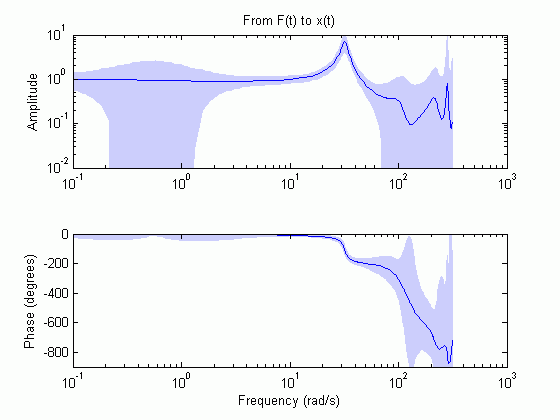
Дополнительные сведения см. в разделе Неопределенность расчетной модели.
Документация System Identification Toolbox предоставляет необходимую информацию для использования данного продукта. Доступны дополнительные ресурсы, которые помогут вам узнать больше о конкретных аспектах теории и приложений идентификации системы.
В следующей книге описаны методы идентификации системы и физического моделирования:
Люнг, Леннарт и Торкель Рад. Моделирование динамических систем. Серия информационных и системных наук Prentice Hall. Энглвуд Клиффс, Нью-Джерси: ПТР Прентис Холл, 1994.
В этих книгах содержится подробная информация о теории и алгоритмах идентификации системы:
Люнг, Леннарт. Идентификация системы: теория для пользователя. Второе издание. Серия информационных и системных наук Prentice Hall. Река Верхнее Седло, Нью-Джерси: PTR Prentice Hall, 1999.
Сёдерстрём, Торстен и Петре Стоика. Идентификация системы. Prentice Hall International Series по проектированию систем и управления. Нью-Йорк: Прентис Холл, 1989.
Сведения о работе с данными частотной области см. в следующей книге:
Пинтелон, Рик и Йохан Шукенс. Идентификация системы. Подход к частотной области. Хобокен, Нью-Джерси: John Wiley & Sons, 2001. https://doi.org/10.1002/0471723134.
Сведения о нелинейной идентификации см. в следующих ссылках:
Шёберг, Йонас, Цинхуа Чжан, Леннарт Льюн, Альберт Бенвенисте, Бернар Делён, Пьер-Ив Глореннец, Хокан Хьялмарссон, и Анатоли Юдицкий. «Нелинейное моделирование черного ящика в идентификации системы: унифицированный обзор». Automatica 31, no. 12 (декабрь 1995): 1691-1724. https://doi.org/10.1016/0005-1098 (95) 00120-8.
Юдицкий, Анатолий, Хокан Хьяльмарссон, Альберт Бенвенисте, Бернард Делён, Леннарт Льюн, Йонас Шёберг, и Цинхуа Чжан. «Нелинейные модели черных ящиков в системной идентификации: математические основы». Automatica 31, No 12 (декабрь 1995): 1725-50. https://doi.org/10.1016/0005-1098 (95) 00119-1.
Чжан, Цинхуа и Альберт Бенвенистэ. «Вейвлет-сети». Сделки IEEE по нейронным сетям 3, № 6 (ноябрь 1992 года): 889-98. https://doi.org/10.1109/72.165591.
Чжан, Цинхуа. «Использование вейвлет-сети в непараметрической оценке». Сделки IEEE по нейронным сетям 8, № 2 (март 1997 года): 227-36. https://doi.org/10.1109/72.557660.
Для получения дополнительной информации о системах и сигналах см. следующую книгу:
Оппенгейм, Алан В. и Алан С. Вилльский, «Сигналы и системы». Река Верхнее Седло, Нью-Джерси: PTR Prentice Hall, 1985.
В следующем учебнике описаны численные методы оценки параметров с использованием минимизации критерия:
Деннис, Дж. Э., младший и Роберт Б. Шнабель. Численные методы для неограниченной оптимизации и нелинейных уравнений. Река Верхнее Седло, Нью-Джерси: PTR Prentice Hall, 1983.