Шина (магическая формула)

Шина с продольным поведением, заданным коэффициентами магической формулы

Библиотека:
Simscape/Трансмиссия/Шины и транспортные средства

Описание

Блок Tire (Magic Formula) моделирует шину с продольным поведением, заданным магической формулой [1], эмпирическим уравнением, основанным на четырех коэффициентах подгонки. Блок может моделировать динамику шин в постоянных или переменных условиях дорожного покрытия.

Продольное направление шины такое же, как и направление ее движения, когда она катится по дорожному покрытию. Этот блок является структурным компонентом, основанным на блоке взаимодействия шин и дорог (Magic Formula).

Для повышения точности модели шины можно задать такие свойства, как податливость шины, инерция и сопротивление качению. Однако эти свойства увеличивают сложность модели шины и могут замедлить моделирование. При моделировании модели в режиме реального времени или при подготовке модели к аппаратному моделированию в цикле (HIL) следует учитывать ее соответствие и инерцию.

Модель шины

Блок Tire (Magic Formula) моделирует шину как жесткую комбинацию колесо-шина в контакте с дорогой и подверженную скольжению. Когда крутящий момент прикладывается к оси колеса, шина толкает на землю (при этом подвергаясь контактному трению) и передает результирующую реакцию как усилие назад на колесо. Это действие толкает колесо вперед или назад. Если включить дополнительное соответствие шины, шина также гибко деформируется под нагрузкой.

На рисунке показаны силы, действующие на шину. Таблица определяет переменные модели шины.

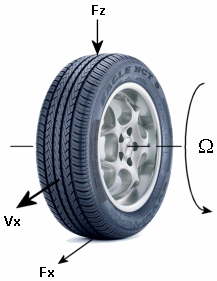
Переменные модели шины

Символ	Описание и единица измерения
_rw	Радиус колеса
_Vx	Продольная скорость ступицы колеса
u	Продольная деформация шины
Ω	Угловая скорость колеса
Ω′	Угловая скорость точки контакта. Если нет продольной деформации шины, то есть если $u =$ 0 $,^{}$ Ω′=Ω.
$_{} {rwΛ}^{}$ ′	Продольная скорость протектора шины
$_{Vsx} =_{} {rwΛ}_{}$ − Vx	Скорость скольжения колеса
${^{}}_{}_{}^{}_{V′sx=rwΩ′−Vx}$	Скорость проскальзывания контакта. Если нет продольной деформации шины, то есть если $u =$ 0 ${,^{}}_{}_{}$ V′sx=Vsx.
$k \frac{=_{}}{_{}}$ Vsx 'Vx \|	Проскальзывание колеса
$^{} \frac{{^{}}_{}}{_{} k'=V'sx'Vx\|}$	Контактная накладная. Если нет продольной деформации шины, то есть если $u =$ 0 $,^{}$ k′=k.
_Vth	Пороговая скорость ступицы колеса
_Fz	Вертикальная нагрузка на шину
_Fx	Продольное усилие, прикладываемое к шине в точке контакта
$_{_{CFx}} {= \frac{(_{}}{}}_{∂Fx∂u}$ ) 0	Продольная жесткость шины при деформации
$_{_{bFx}} {= \frac{(_{}}{\overset{}{}}}_{∂Fx∂u˙}$ ) 0	Продольное демпфирование шины при деформации
_Iw	Инерция колеса-шины, при которой эффективная масса равна $\frac{_{}}{_{}^{Iwrw2}}$
_τdrive	Крутящий момент, прилагаемый осью к колесу

Кинематика и реакция шин

Крен и скольжение

Несклеиваемая шина будет вращаться и преобразовываться как $_{Vx} =_{}$ rwΛ. Однако, когда шины скользят, они реагируют, развивая продольную силу, Fx.

Скорость скольжения колеса составляет $_{Vsx} =_{} {rwΛ}_{}$ − Vx. Проскальзывание колеса $\frac{k_{}}{=_{}}$ Vsx 'Vx |. Для заблокированного скользящего колеса k = − 1. Для идеальной прокатки k = 0.

Проскальзывание на низкой скорости

Для низких скоростей, определяемых $_{}_{} |Vx|\leq|Vth|,$ проскальзывание колеса становится следующим:

$k \frac{=_{}}{{2Vsx}_{(} \frac{_{Vth}^{}}{+_{}}}$ Vx2Vth)

Эта модификация допускает несингулярное, ненулевое скольжение при нулевой скорости колеса. Например, для идеального проскальзывания, то есть в случае нетранслирующей вращающейся шины, $_{Vx} =$ 0, $в то время как \frac{k_{=}}{_{}}$ 2rwStartVth является конечным.

Деформация

Если шина смоделирована с соблюдением требований, она также является гибкой. В этом случае, поскольку шина деформируется, точка контакта шины с дорогой поворачивается с немного отличающейся угловой скоростью, Λ ′, от колеса, Λ, и требует, вместо проскальзывания колеса, точки контакта или проскальзывания контактной накладки . κ'. Блок моделирует деформирующую шину как поступательную пружинную заслонку жесткости, _{_CFx} и демпфирования, _{_bFx}.

Если моделировать шину без соответствия, то есть если $u =$ 0, то продольная деформация шины отсутствует в любое время при моделировании и:

$^{} k′=k$
${^{}}_{}_{V′sx=Vsx}$
$^{} Ω′=Ω$

Динамика шин и колес

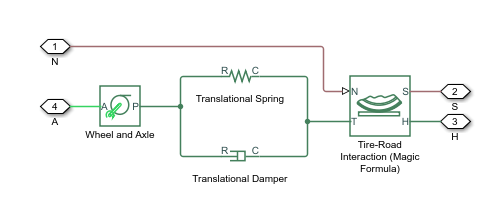
Полная модель шины эквивалентна этой диаграмме компонента Simscape™/Simscape Driveline™. Он моделирует как переходное, так и стационарное поведение и правильно представляет начало и начало остановки. Поступательная пружина и поступательная заслонка эквивалентны жесткости шины _{_CFx} и демпфированию _{_bFx}. Блок взаимодействия шин и дорог (Magic Formula) моделирует продольную силу _Fx на шине как функцию _Fz и k ′ используя магическую формулу, с k ′ в качестве независимой переменной скольжения.

Радиус колеса и оси - это радиус колеса _rw. Значение Масса (Mass) - это эффективная масса, $\frac{_{}}{_{}^{Iwrw2}}$ . Функция f (k ′, Fz) характеристики шины определяет продольное усилие Fx. Вместе с крутящим моментом карданного вала, приложенным к оси колеса, Fx определяет угловое и продольное движение колеса.

Без соответствия шин поступательная пружина и поступательная заслонка опущены, а контактные переменные возвращаются к переменным колес. В этом случае шина эффективно имеет бесконечную жесткость, и порт P колеса и оси соединяется непосредственно с портом T взаимодействия шины и дороги (Magic Formula).

Без инерции шины масса опускается.

Допущения и ограничения

Блок Tire (Magic Formula) принимает только продольное движение и не включает разворот, поворот или боковое движение.
Податливость шины подразумевает задержку во времени реакции шины на силы, действующие на нее. Моделирование временных задержек повышает точность модели, но снижает производительность моделирования. См. раздел Корректировка точности модели.

Порты

Вход

развернуть все

`N` - Нормальная сила
физический сигнал

Порт ввода физического сигнала, связанный с нормальной силой, действующей на шину. Нормальная сила является положительной, если она действует вниз на шину, прижимая ее к дорожному покрытию.

`M` - Коэффициенты магической формулы
физический сигнал | вектор | [B, C, D, E]

Порт ввода физического сигнала, связанный с коэффициентами магической формулы. Предоставьте коэффициенты магической формулы в виде четырехэлементного вектора, указанного в порядке [B, C, D, E].

Зависимости

Порт M открывается только в том случае, если для параметра Main > Parameterize by установлено значение Physical signal Magic Formula coefficients. Дополнительные сведения см. в разделе Зависимости основных параметров.

Продукция

развернуть все

`S` - Проскальзывание
физический сигнал

Порт вывода физического сигнала, связанный с относительным проскальзыванием между шиной и дорогой.

Сохранение

развернуть все

`A` - Ось
механическое вращение

Механическое поворотное отверстие, связанное с осью, на которой сидит шина.

`H` - Концентратор
механический поступательный

Механическое поступательное отверстие, связанное со ступицей колеса, которое передает тягу, создаваемую шиной, оставшейся части транспортного средства.

Параметры

развернуть все

Главный

В таблице показано, как видимость некоторых основных параметров зависит от параметров, выбранных для других параметров. Сведения о прочтении таблицы см. в разделе Зависимости параметров.

Зависимости основных параметров

Главный
Параметризовать по - Выбрать `Peak longitudinal force and corresponding slip`, `Constant Magic Formula coefficients`, `Load-dependent Magic Formula coefficients`, или `Physical signal Magic Formula coefficients`
Максимальное продольное усилие и соответствующее скольжение	Коэффициенты постоянной магической формулы	Зависящие от нагрузки коэффициенты магической формулы	Коэффициенты формулы магии физического сигнала - предоставляет входной порт M физического сигнала для предоставления коэффициентов формулы магии блоку в виде массива элементов в этом порядке [B, C, D, E].
Номинальная вертикальная нагрузка	Коэффициент магической формулы B	Параметр C-коэффициента магической формулы, p_Cx1
Пиковая продольная сила при номинальной нагрузке	Коэффициент магической формулы C	Параметры D-коэффициентов магической формулы, [p_Dx1 p_Dx2]
Проскальзывание при пиковой силе при номинальной нагрузке (в процентах)	Коэффициент магической формулы D	Параметры E-коэффициентов магической формулы, [p_Ex1 p_Ex2 p_Ex3 p_Ex4]
	Коэффициент магической формулы E	Параметры BCD-коэффициента магической формулы, [p_Kx1 p_Kx2 p_Kx3]
		Параметры H-коэффициентов магической формулы, [p_Hx1 p_Hx2]
		Параметры V-коэффициентов магической формулы, [p_Vx1 p_Vx2]

`Parameterize by` - Метод параметризации
`Peak longitudinal force and corresponding slip` (по умолчанию) | `Constant Magic Formula coefficients` | `Load-dependent Magic Formula coefficients` | `Physical signal Magic Formula coefficients`

Модель взаимодействия шины с дорогой Magic Formula.

Для моделирования динамики шин в постоянных условиях дорожного покрытия выберите одну из следующих моделей:

Peak longitudinal force and corresponding slip - Параметризация магической формулы с физическими характеристиками шины.
Constant Magic Formula coefficients - Укажите параметры, определяющие коэффициенты B, C, D и E в виде скаляров с этими значениями по умолчанию.

Коэффициент Значение по умолчанию
B 10
C 1.9
D 1
E 0.97

Коэффициент	Значение по умолчанию
B	`10`
C	`1.9`
D	`1`
E	`0.97`

Load-dependent Magic Formula coefficients - Укажите параметры, определяющие зависящие от нагрузки коэффициенты C, D, E, K, H и V как векторы, по одному для каждого коэффициента, с этими значениями по умолчанию.

Коэффициент	Параметры	Значения по умолчанию
C	p_Cx1	1.685
D	[p_Dx1 p_Dx2]	[ 1.21 –0.037 ]
E	[p_Ex1 p_Ex2 p_Ex3 p_Ex4]	[ 0.344 0.095 –0.02 0 ]
K	[p_Kx1 p_Kx2 p_Kx3]	[ 21.51 –0.163 0.245 ]
H	[p_Hx1 p_Hx2]	[ –0.002 0.002 ]
V	[p_Vx1 p_Vx2]	[ 0 0 ]

Для моделирования динамики шины в переменных условиях дорожного покрытия выберите Physical signal Magic Formula coefficients. Выбор этой модели открывает физический сигнальный порт M. Используйте порт для ввода коэффициентов магической формулы в виде четырехэлементного вектора, заданного в порядке [B, C, D, E].

Зависимости

Каждый параметр метода параметризации предоставляет связанные параметры и скрывает несвязанные параметры. Выбор Physical signal Magic Formula coefficients предоставляет входной порт физического сигнала. Дополнительные сведения см. в разделе Зависимости основных параметров.

`Rated vertical load` - Номинальное усилие нагрузки
`3000` `N` (по умолчанию) | положительный скаляр

Номинальная сила вертикальной нагрузки _Fz0.

Зависимости

Этот параметр отображается только при выборе Peak longitudinal force and corresponding slip метод параметризации. Дополнительные сведения см. в разделе Зависимости основных параметров.

`Peak longitudinal force at rated load` - Максимальное продольное усилие при номинальной нагрузке
`3500` `N` (по умолчанию) | положительный скаляр

Максимальное продольное усилие, _Fx0 на колесо, когда вертикальная нагрузка равна номинальному значению _Fz0.

Зависимости

`Slip at peak force at rated load (percent)` - Процент проскальзывания при максимальной продольной силе и номинальной нагрузке
`10` (по умолчанию) | положительный скаляр

Контактный проскальзывающий элемент/0, выраженный в процентах (%), когда продольная сила равна максимальному значению _Fx0 а вертикальная нагрузка равна номинальному значению _Fz0.

Зависимости

`Magic Formula B coefficient` - Коэффициент постоянной магии формулы B
`10` (по умолчанию) | положительный скаляр

Независимый от нагрузки коэффициент магической формулы B.

Зависимости

Этот параметр отображается только при выборе Constant Magic Formula coefficients метод параметризации. Дополнительные сведения см. в разделе Зависимости основных параметров.

`Magic Formula C coefficient` - Коэффициент постоянной магии формулы C
`1.9` (по умолчанию) | положительный скаляр

Независимый от нагрузки коэффициент магической формулы C.

Зависимости

`Magic Formula D coefficient` - Коэффициент постоянной магии формулы D
`1` (по умолчанию) | положительный скаляр

Независимый от нагрузки коэффициент магической формулы D.

Зависимости

`Magic Formula E coefficient` - Коэффициент постоянной магии формулы E
`0.97` (по умолчанию) | положительный скаляр

Независимый от нагрузки коэффициент магической формулы E.

Зависимости

`Tire nominal vertical load` - Нормальная сила
`4000` `N` (по умолчанию) | положительный скаляр

Номинальное нормальное усилие, _Fz0 на шину.

Зависимости

Этот параметр отображается только при выборе Load-dependent Magic Formula coefficients метод параметризации. Дополнительные сведения см. в разделе Зависимости основных параметров.

`Magic Formula C-coefficient parameter, p_Cx1` - Коэффициент переменной магии формулы C
`1.685` (по умолчанию) | скаляр

Зависящий от нагрузки коэффициент магической формулы C.

Зависимости

`Magic Formula D-coefficient parameters, [p_Dx1 p_Dx2]` - Коэффициент переменной магии формулы D
`[1.21, -.037]` (по умолчанию) | вектор

Зависящий от нагрузки коэффициент магической формулы D.

Зависимости

`Magic Formula E-coefficient parameters, [p_Ex1 p_Ex2 p_Ex3 p_Ex4]` - Коэффициент переменной магической формулы E
`[.344, .095, -.02, 0]` (по умолчанию) | вектор

Зависящий от нагрузки коэффициент магической формулы E.

Зависимости

`Magic Formula BCD-coefficient parameters, [p_Kx1 p_Kx2 p_Kx3]` - Коэффициент переменной магии формулы K
`[21.51, -.163, .245]` (по умолчанию) | вектор

Зависящий от нагрузки коэффициент магической формулы K.

Зависимости

`Magic Formula H-coefficient parameters, [p_Hx1 p_Hx2]` - Коэффициент переменной магии формулы H
`[-.002, .002]` (по умолчанию) | вектор

Зависящий от нагрузки коэффициент магической формулы H.

Зависимости

`Magic Formula V-coefficient parameters, [p_Vx1 p_Vx2]` - Коэффициент переменной магии формулы V
`[0, 0]` (по умолчанию) | вектор

Зависящий от нагрузки коэффициент магической формулы V.

Зависимости

Геометрия

`Rolling radius` - Радиус незагруженного колеса шины
`0.3` `m` (по умолчанию) | положительный скаляр

Радиус разгруженного колеса шины, _изб.

Динамика

В таблице показано, как видимость некоторых параметров Dynamics зависит от параметров, выбранных для других параметров. Сведения о прочтении таблицы см. в разделе Зависимости параметров.

Зависимости параметров Dynamics

Динамика
Соответствие нормативным требованиям - Выберите `No compliance - Suitable for HIL simulation` или `Specify stiffness and damping`
Отсутствие соответствия - подходит для моделирования HIL	Задание жесткости и демпфирования
	Продольная жесткость
	Продольное демпфирование
Инерция - выбор `No Inertia` или `Specify inertia and initial velocity`
Отсутствие инерции	Указать инерцию и начальную скорость
	Инерция шины
	Начальная скорость

`Compliance` - Динамическая модель соответствия
`No compliance - Suitable for HIL simulation` (по умолчанию) | `Specify stiffness and damping`

Модель динамического соответствия шины.

No compliance - Suitable for HIL simulation - Шина моделируется без динамического соответствия.
Specify stiffness and damping Шина смоделирована как жесткая, демпфирующая пружина и деформируется под нагрузкой.

Зависимости

Выбор Specify stiffness and damping способ параметризации, раскрывает параметры жесткости и демпфирования. Дополнительные сведения см. в разделе Зависимости параметров Dynamics.

`Longitudinal stiffness` - Продольная жесткость
`1e6` `N/m` (по умолчанию) | положительный скаляр

Продольная жесткость шины _CFx.

Зависимости

Выбор Specify stiffness and damping для параметра Compliance предоставляет этот параметр. Дополнительные сведения см. в разделе Зависимости параметров Dynamics.

`Longitudinal damping` - Продольное демпфирование
`1000` `N/(m/s)` (по умолчанию) | положительный скаляр

Продольное демпфирование шины _bFx.

Зависимости

`Inertia` - Инерционная модель
`No inertia` (по умолчанию) | `Specify inertia and initial velocity`

Модель инерции вращения шины.

No inertia - Шина моделируется без динамического соответствия.
Specify inertia and initial velocity Шина смоделирована как жесткая, демпфирующая пружина и деформируется под нагрузкой.

Зависимости

Выбор Specify inertia and initial velocity способ параметризации, раскрывает параметры инерции и скорости. Дополнительные сведения см. в разделе Зависимости параметров Dynamics.

`Tire inertia` - Инерция вращения
`1` `kg*m^2` (по умолчанию) | положительный скаляр

Инерция вращения _Iw колесно-шинного узла.

Зависимости

Выбор Specify inertia and initial velocity для параметра Инерция (Inertia) отображает этот параметр. Дополнительные сведения см. в разделе Зависимости параметров Dynamics.

`Initial velocity` - Начальная скорость вращения
`0` `rad/s` (по умолчанию) | скаляр

Исходная угловая скорость, Λ (0), шины.

Зависимости

Сопротивление качению

В таблице показано, как видимость некоторых параметров зависит от параметров, выбранных для других параметров. Сведения о прочтении таблицы см. в разделе Зависимости параметров.

Зависимости параметров сопротивления качению

Сопротивление качению
Сопротивление качению - выбор `Off` или `On`
Прочь	На
	Модель сопротивления - выбор `Constant coefficient` или `Pressure and velocity dependent`
	Постоянный коэффициент	Давление и скорость зависят
	Постоянный коэффициент	Давление в шинах
		Альфа
		Бета
		Коэффициент А
		Коэффициент B
		Коэффициент C
	Порог скорости

`Rolling resistance` - Вариант сопротивления качению
`Off` (по умолчанию) | `On`

Варианты моделирования сопротивления качению:

Off - Пренебречь сопротивлением качению.
On - Включить сопротивление качению.

Зависимости

Выбор On раскрывает параметры сопротивления качению. Дополнительные сведения см. в разделе Зависимости параметров сопротивления качению.

`Resistance model` - Модель сопротивления качению
`Constant coefficient` (по умолчанию) | `Pressure and velocity dependent`

Модель сопротивления качению шины.

Constant coefficient - Пренебречь сопротивлением качению.
Pressure and velocity dependent - Включить сопротивление качению.

Зависимости

Каждая опция модели сопротивления предоставляет связанные параметры. Дополнительные сведения см. в разделе Зависимости параметров сопротивления качению.

`Constant coefficient` - Константа пропорциональности
`0.015` (по умолчанию) | положительный скаляр

Коэффициент, устанавливающий пропорциональность между нормальной силой и силой сопротивления качению. Параметр должен быть больше нуля.

Зависимости

Выбор On для параметра сопротивления качению и Constant coefficient для параметра модели сопротивления представляет этот параметр. Дополнительные сведения см. в разделе Зависимости параметров сопротивления качению.

`Tire pressure` - Давление в шинах
`250e3` `Pa` (по умолчанию) | положительный скаляр

Давление накачки шины. Параметр должен быть больше нуля.

Зависимости

Выбор On для параметра сопротивления качению и Pressure and velocity dependent для параметра модели сопротивления представляет этот параметр. Дополнительные сведения см. в разделе Зависимости параметров сопротивления качению.

`Alpha` - Показатель уравнения давления в шинах
`-0.003` (по умолчанию) | скаляр

Показатель давления в шине в уравнении модели.

Зависимости

`Beta` - экспонента уравнения нормальной силы
`0.97` (по умолчанию) | скаляр

Экспонента уравнения модели нормальной силы.

Зависимости

`Coefficient A` - Независимый от скорости компонент силы A
`84e-4` (по умолчанию)

Независимый от скорости компонент силы в уравнении модели. Параметр должен быть больше нуля.

Зависимости

`Coefficient B` - Зависящая от скорости составляющая силы B
`6.2e-4` `s/m` (по умолчанию) | положительный скаляр

Зависящая от скорости составляющая силы в уравнении модели. Параметр должен быть больше нуля.

Зависимости

`Coefficient C` - Зависящая от скорости составляющая силы C
`1.6e-4` `s^2/m^2` (по умолчанию) | положительный скаляр

Компонент силы, который зависит от квадрата члена скорости в уравнении модели. Параметр должен быть больше нуля.

Зависимости

`Velocity threshold` - Порог скорости ступицы колеса для математической модели скольжения
`0.001` `m/s` (по умолчанию) | положительный скаляр

Скорость, при которой полная сила сопротивления качению передается на ступицу качения. Параметр обеспечивает непрерывность усилия при изменении направления скорости, что повышает численную стабильность моделирования. Параметр должен быть больше нуля.

Зависимости

Выбор On для параметра сопротивления качению этот параметр отображается. Дополнительные сведения см. в разделе Зависимости параметров сопротивления качению.

Расширенный

`Velocity threshold` - Порог скорости ступицы колеса для математической модели скольжения
`0.1` `m/s` (по умолчанию) | положительный скаляр

Скорость ступицы колеса _Vth, ниже которой изменяется расчет скольжения, чтобы избежать сингулярного изменения при нулевой скорости. Должно быть положительно.

Примеры модели

Дифференциал ограниченного проскальзывания с муфтами

Сравнение поведения разомкнутого дифференциала и дифференциала с ограниченным проскальзыванием с пакетами сцепления. Дифференциал ограниченного проскальзывания моделируется с использованием компонентов из библиотеки Gears и библиотеки Clutches в Simscape™ Driveline™. Скольжение колеса ограничено сцеплениями, которые входят в зацепление, когда крутящий момент, приложенный к входу дифференциала, превышает порог. Муфты блокируют дифференциал так, чтобы выходные валы дифференциала вращались с одинаковой скоростью.

Дифференциал Торсена

Сравнение поведения разомкнутого дифференциала и дифференциала с ограниченным проскальзыванием Торсена. Дифференциал Торсена моделируется с использованием компонентов из библиотеки зубчатых колес в Simscape™ Driveline™. Проскальзывание ограничено в дифференциале Торсена, поскольку в нём используются невозвратные червячные передачи, которые моделируются компонентами Sun-Planet Worm Gear. Результатом является более высокий крутящий момент, прилагаемый к колесу с большей тягой, и идентичные скорости для левой и правой осей.

Транспортное средство с коробкой передач с двойным сцеплением

Транспортное средство с пятиступенчатой автоматической коробкой передач с двойным сцеплением. Контроллер трансмиссии преобразует отклонение педали в требуемый крутящий момент. Этот требуемый крутящий момент затем передается на управление двигателем. Отклонение педали и скорость транспортного средства также используются контроллером трансмиссии для определения того, когда должны происходить переключения передач. Переключения передач осуществляются через две муфты, при этом давление одной муфты увеличивается, когда давление другой муфты снижается. Предварительный выбор передачи с помощью собачьих муфт гарантирует, что правильная передача будет полностью выбрана до включения постоянной муфты.

Транспортное средство с четырехступенчатой трансмиссией

Комплектное транспортное средство с Simscape™ Driveline™ компонентами, включая двигатель, трансмиссию, четырехступенчатую трансмиссию, шины и продольную динамику транспортного средства. Контроллер трансмиссии реализован как конечный автомат в Stateflow ®, выбирая передачу на основе дроссельной заслонки и скорости транспортного средства.

Транспортное средство с полным приводом

Полноприводное транспортное средство, начинающееся с покоя и поднимающееся с наклоном на 15 градусов. Первоначально транспортное средство катится назад до тех пор, пока двигатель не создаст достаточный крутящий момент для противодействия наклону. Динамика соответствия шин может быть видна, когда транспортное средство начинает ускоряться. Вариант модели, выбранный для всех шин, может быть установлен в модели шин Simple, Friction Parameterized или Magic Formula с использованием гиперссылок в модели.

Подробнее

развернуть все

Моделирование в режиме реального времени и аппаратное моделирование

Для оптимальной производительности моделирования задайте для параметра Dynamics > Compliance значение No compliance - Suitable for HIL simulation.

Ссылки

[1] Pacejka, H.B. Tire and Vehicle Dynamics. Elsevier Science, 2005.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™

См. также

Шина (с параметризацией трения) | Шина (простая) | Взаимодействие шин и дорог (магическая формула)

Темы

Представлен в R2011a

Документация

Шина (магическая формула)

Описание

Модель шины

Кинематика и реакция шин

Динамика шин и колес

Допущения и ограничения

Порты

Вход

N - Нормальная сила физический сигнал

M - Коэффициенты магической формулы физический сигнал | вектор | [B, C, D, E]

Зависимости

Продукция

S - Проскальзывание физический сигнал

Сохранение

A - Ось механическое вращение

H - Концентратор механический поступательный

Параметры

Главный

Parameterize by - Метод параметризации Peak longitudinal force and corresponding slip (по умолчанию) | Constant Magic Formula coefficients | Load-dependent Magic Formula coefficients | Physical signal Magic Formula coefficients

Зависимости

Rated vertical load - Номинальное усилие нагрузки 3000 N (по умолчанию) | положительный скаляр

Зависимости

Peak longitudinal force at rated load - Максимальное продольное усилие при номинальной нагрузке 3500 N (по умолчанию) | положительный скаляр

Зависимости

Slip at peak force at rated load (percent) - Процент проскальзывания при максимальной продольной силе и номинальной нагрузке 10 (по умолчанию) | положительный скаляр

Зависимости

Magic Formula B coefficient - Коэффициент постоянной магии формулы B 10 (по умолчанию) | положительный скаляр

Зависимости

Magic Formula C coefficient - Коэффициент постоянной магии формулы C 1.9 (по умолчанию) | положительный скаляр

Зависимости

Magic Formula D coefficient - Коэффициент постоянной магии формулы D 1 (по умолчанию) | положительный скаляр

Зависимости

Magic Formula E coefficient - Коэффициент постоянной магии формулы E 0.97 (по умолчанию) | положительный скаляр

Зависимости

Tire nominal vertical load - Нормальная сила 4000 N (по умолчанию) | положительный скаляр

Зависимости

Magic Formula C-coefficient parameter, p_Cx1 - Коэффициент переменной магии формулы C 1.685 (по умолчанию) | скаляр

Зависимости

Magic Formula D-coefficient parameters, [p_Dx1 p_Dx2] - Коэффициент переменной магии формулы D [1.21, -.037] (по умолчанию) | вектор

Зависимости

Magic Formula E-coefficient parameters, [p_Ex1 p_Ex2 p_Ex3 p_Ex4] - Коэффициент переменной магической формулы E [.344, .095, -.02, 0] (по умолчанию) | вектор

Зависимости

Magic Formula BCD-coefficient parameters, [p_Kx1 p_Kx2 p_Kx3] - Коэффициент переменной магии формулы K [21.51, -.163, .245] (по умолчанию) | вектор

Зависимости

Magic Formula H-coefficient parameters, [p_Hx1 p_Hx2] - Коэффициент переменной магии формулы H [-.002, .002] (по умолчанию) | вектор

Зависимости

Magic Formula V-coefficient parameters, [p_Vx1 p_Vx2] - Коэффициент переменной магии формулы V [0, 0] (по умолчанию) | вектор

Зависимости

Геометрия

Rolling radius - Радиус незагруженного колеса шины 0.3 m (по умолчанию) | положительный скаляр

Динамика

Compliance - Динамическая модель соответствия No compliance - Suitable for HIL simulation (по умолчанию) | Specify stiffness and damping

Зависимости

Longitudinal stiffness - Продольная жесткость 1e6 N/m (по умолчанию) | положительный скаляр

Зависимости

Longitudinal damping - Продольное демпфирование 1000 N/(m/s) (по умолчанию) | положительный скаляр

Зависимости

Inertia - Инерционная модель No inertia (по умолчанию) | Specify inertia and initial velocity

Зависимости

Tire inertia - Инерция вращения 1 kg*m^2 (по умолчанию) | положительный скаляр

Зависимости

Initial velocity - Начальная скорость вращения 0 rad/s (по умолчанию) | скаляр

Зависимости

Сопротивление качению

Rolling resistance - Вариант сопротивления качению Off (по умолчанию) | On

Зависимости

Resistance model - Модель сопротивления качению Constant coefficient (по умолчанию) | Pressure and velocity dependent

Зависимости

Constant coefficient - Константа пропорциональности 0.015 (по умолчанию) | положительный скаляр

Зависимости

Tire pressure - Давление в шинах 250e3 Pa (по умолчанию) | положительный скаляр

Зависимости

Alpha - Показатель уравнения давления в шинах -0.003 (по умолчанию) | скаляр

Зависимости

Beta - экспонента уравнения нормальной силы 0.97 (по умолчанию) | скаляр

Зависимости

Coefficient A - Независимый от скорости компонент силы A 84e-4 (по умолчанию)

Зависимости

Coefficient B - Зависящая от скорости составляющая силы B 6.2e-4 s/m (по умолчанию) | положительный скаляр

`N` - Нормальная сила
физический сигнал

`M` - Коэффициенты магической формулы
физический сигнал | вектор | [B, C, D, E]

`S` - Проскальзывание
физический сигнал

`A` - Ось
механическое вращение

`H` - Концентратор
механический поступательный

`Parameterize by` - Метод параметризации
`Peak longitudinal force and corresponding slip` (по умолчанию) | `Constant Magic Formula coefficients` | `Load-dependent Magic Formula coefficients` | `Physical signal Magic Formula coefficients`

`Rated vertical load` - Номинальное усилие нагрузки
`3000` `N` (по умолчанию) | положительный скаляр

`Peak longitudinal force at rated load` - Максимальное продольное усилие при номинальной нагрузке
`3500` `N` (по умолчанию) | положительный скаляр

`Slip at peak force at rated load (percent)` - Процент проскальзывания при максимальной продольной силе и номинальной нагрузке
`10` (по умолчанию) | положительный скаляр

`Magic Formula B coefficient` - Коэффициент постоянной магии формулы B
`10` (по умолчанию) | положительный скаляр

`Magic Formula C coefficient` - Коэффициент постоянной магии формулы C
`1.9` (по умолчанию) | положительный скаляр

`Magic Formula D coefficient` - Коэффициент постоянной магии формулы D
`1` (по умолчанию) | положительный скаляр

`Magic Formula E coefficient` - Коэффициент постоянной магии формулы E
`0.97` (по умолчанию) | положительный скаляр

`Tire nominal vertical load` - Нормальная сила
`4000` `N` (по умолчанию) | положительный скаляр

`Magic Formula C-coefficient parameter, p_Cx1` - Коэффициент переменной магии формулы C
`1.685` (по умолчанию) | скаляр

`Magic Formula D-coefficient parameters, [p_Dx1 p_Dx2]` - Коэффициент переменной магии формулы D
`[1.21, -.037]` (по умолчанию) | вектор

`Magic Formula E-coefficient parameters, [p_Ex1 p_Ex2 p_Ex3 p_Ex4]` - Коэффициент переменной магической формулы E
`[.344, .095, -.02, 0]` (по умолчанию) | вектор

`Magic Formula BCD-coefficient parameters, [p_Kx1 p_Kx2 p_Kx3]` - Коэффициент переменной магии формулы K
`[21.51, -.163, .245]` (по умолчанию) | вектор

`Magic Formula H-coefficient parameters, [p_Hx1 p_Hx2]` - Коэффициент переменной магии формулы H
`[-.002, .002]` (по умолчанию) | вектор

`Magic Formula V-coefficient parameters, [p_Vx1 p_Vx2]` - Коэффициент переменной магии формулы V
`[0, 0]` (по умолчанию) | вектор

`Rolling radius` - Радиус незагруженного колеса шины
`0.3` `m` (по умолчанию) | положительный скаляр

`Compliance` - Динамическая модель соответствия
`No compliance - Suitable for HIL simulation` (по умолчанию) | `Specify stiffness and damping`

`Longitudinal stiffness` - Продольная жесткость
`1e6` `N/m` (по умолчанию) | положительный скаляр

`Longitudinal damping` - Продольное демпфирование
`1000` `N/(m/s)` (по умолчанию) | положительный скаляр

`Inertia` - Инерционная модель
`No inertia` (по умолчанию) | `Specify inertia and initial velocity`

`Tire inertia` - Инерция вращения
`1` `kg*m^2` (по умолчанию) | положительный скаляр

`Initial velocity` - Начальная скорость вращения
`0` `rad/s` (по умолчанию) | скаляр

`Rolling resistance` - Вариант сопротивления качению
`Off` (по умолчанию) | `On`

`Resistance model` - Модель сопротивления качению
`Constant coefficient` (по умолчанию) | `Pressure and velocity dependent`

`Constant coefficient` - Константа пропорциональности
`0.015` (по умолчанию) | положительный скаляр

`Tire pressure` - Давление в шинах
`250e3` `Pa` (по умолчанию) | положительный скаляр

`Alpha` - Показатель уравнения давления в шинах
`-0.003` (по умолчанию) | скаляр

`Beta` - экспонента уравнения нормальной силы
`0.97` (по умолчанию) | скаляр

`Coefficient A` - Независимый от скорости компонент силы A
`84e-4` (по умолчанию)

`Coefficient B` - Зависящая от скорости составляющая силы B
`6.2e-4` `s/m` (по умолчанию) | положительный скаляр

`Coefficient C` - Зависящая от скорости составляющая силы C
`1.6e-4` `s^2/m^2` (по умолчанию) | положительный скаляр

`Velocity threshold` - Порог скорости ступицы колеса для математической модели скольжения
`0.001` `m/s` (по умолчанию) | положительный скаляр

`Velocity threshold` - Порог скорости ступицы колеса для математической модели скольжения
`0.1` `m/s` (по умолчанию) | положительный скаляр

Создание кода C/C + +
Создайте код C и C++ с помощью Simulink ® Coder™