6DOF ECEF (Quaternion)

Реализуйте кватернионное представление уравнений движения с шестью степенями свободы в координатах ECEF

Библиотека:
Аэрокосмический Уравнения Движения/ 6DOF

Описание

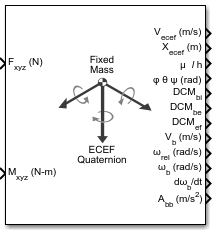
Блок 6DOF ECEF (Quaternion) Реализуйте кватернионное представление уравнений движения с шестью степенями свободы в координатах Earth-fixed (ECEF) с центром Земли. В нем рассматривается вращение координатной системы координат ECEF (_{XECEF, YECEF, ZECEF}) вокруг системы координат ECI (_{XECI, YECI, ZECI}). Источником координатной системы координат ECEF является центр Земли. Для получения дополнительной информации о координатной системе координат ECEF см. «Алгоритмы».

Ограничения

Эта реализация принимает, что приложенные силы действуют в центре тяжести тела, и что масса и инерция постоянны.
Эта реализация генерирует геодезическую широту, которая лежит между ± 90 степенями, и долготу, которая лежит между ± 180 степенями. Кроме того, высота MSL приблизительная.
Земля принята эллипсоидальной. Путем установки уплощения на 0,0 может быть достигнута сферическая планета. Прецессией, нутацией и полярным движением Земли пренебрегают. Небесная долгота Гринвича - среднее сидереальное время Гринвича (GMST) и обеспечивает грубое приближение к сидерическому времени.
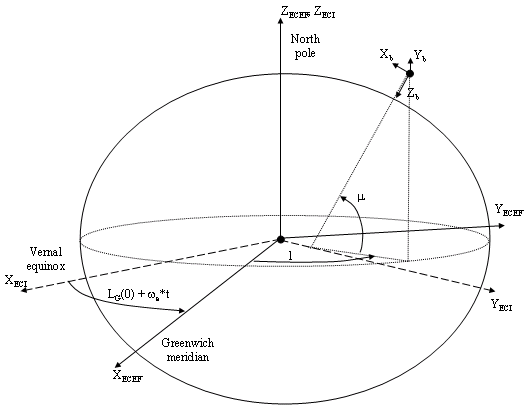
Реализация системы координат ECEF предполагает, что источник находится в центре планеты, ось x пересекает меридиан Гринвича и экватор, ось z является средней осью вращения планеты, положительной к северу, а ось y завершает правую систему.
Реализация системы координат ECI принимает, что источник находится в центре планеты, x -ось является продолжением линии от центра Земли к весеннему равноденствию, z -ось указывает в направлении северного полюса средней экваториальной плоскости, положительный на север, и ось y завершает правую систему.

Порты

Вход

расширить все

`_Fxyz` - Приложенные силы
трехэлементный вектор

Приложенные силы, заданные как трехэлементный вектор.

Типы данных: double

`_Mxyz` - Приложенные моменты
трехэлементный вектор

Приложенные моменты, заданные как трехэлементный вектор.

Типы данных: double

`_LG(0)` - Начальная небесная долгота Гринвича
скаляр

Гринвичский меридиан начальный угол небесной долготы, заданный как скаляр.

Зависимости

Чтобы включить этот порт, установите Celestial longitude of Greenwich равным External.

Типы данных: double

Выход

расширить все

`_Vecef` - Скорость тела относительно системы координат ECEF,
трехэлементный вектор

Скорость тела относительно системы координат ECEF, выраженная в системе координат ECEF, возвращается как трехэлементный вектор.

Типы данных: double

`_Xecef` - Положение в системе координат ECEF
трехэлементный вектор

Положение в опорной системе координат ECEF, возвращаемое как трехэлементный вектор.

Типы данных: double

`μ l h` - Положение в геодезической широте, долготе и высоте
трехэлементный вектор | M-by-3 массив

Положение в геодезической широте, долготе и высоте, в степенях, возвращается в виде трехэлементного вектора или M-by-3 массива, в выбранных модулях длины, соответственно.

Типы данных: double

`φ θ Ψ (rad)` - Углы поворота тела
трехэлементный вектор

Углы поворота тела [крен, тангаж, рыскание], возвращаемые в виде трехэлементного вектора, в радианах. Углы поворота Эйлера являются углами между телом и системами координат NED.

Типы данных: double

`_DCMbi` - Преобразование координат из осей ECI
Матрица 3 на 3

Преобразование координат из осей ECI в фиксированные по телу оси, возвращаемое как матрица 3 на 3.

Типы данных: double

`_DCMbe` - Преобразование координат из осей NED
Матрица 3 на 3

Преобразование координат из осей NED в фиксированные по телу оси, возвращаемое как матрица 3 на 3.

Типы данных: double

`_DCMef` - Преобразование координат из осей ECEF
Матрица 3 на 3

Преобразование координат из осей ECEF в оси NED, возвращаемое как матрица 3 на 3.

Типы данных: double

`_Vb` - Скорость тела относительно системы координат ECEF
трехэлементный вектор

Скорость тела относительно системы координат ECEF, возвращаемая как трехэлементный вектор.

Типы данных: double

`_ωrel` - Относительные угловые скорости тела относительно система координат
трехэлементный вектор

Относительные угловые скорости тела относительно NED системы координат, выраженные в каркасе кузова и возвращенные как трехэлементный вектор, в радианах в секунду.

Типы данных: double

`_ωb` - Угловые скорости тела относительно системы координат ECI
трехэлементный вектор

Угловые скорости тела относительно системы координат ECI, выраженные в каркасе кузова и возвращенные как трехэлементный вектор, в радианах в секунду.

Типы данных: double

`_dωb/dt` - Угловые ускорения корпуса относительно системы координат ECI
трехэлементный вектор

Угловые ускорения тела относительно системы координат ECI, выраженные в каркасе кузова и возвращенные как трехэлементный вектор, в радианах в секунду за секунду.

Типы данных: double

`_Abb` - Ускорения в неподвижных осях тела
трехэлементный вектор

Ускорения тела относительно координатной системы координат ECEF, возвращенные как трехэлементный вектор.

Типы данных: double

`_{Ab ecef}` - Ускорения в неподвижных осях тела
трехэлементный вектор

Ускорения в фиксированных по телу осях относительно системы координат ECEF, возвращенные как трехэлементный вектор.

Зависимости

Чтобы включить эту точку, Include inertial acceleration.

Типы данных: double

Параметры

расширить все

Главный

`Units` - Входные и выходные модули
`Metric (MKS)` (по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

Входной и выходной модули, заданные как Metric (MKS), English (Velocity in ft/s), или English (Velocity in kts).

Модули	Силы	Момент	Ускорение	Скорость	Положение	Масса	Инерция
`Metric (MKS)`	Ньютон	Ньютон-метр	Метры в секунду за секунду	Метры в секунду	Метры	Килограмм	Килограмм-метр в квадрате
`English (Velocity in ft/s)`	Фунт	Фут-фунт	Футы в секунду за секунду	Футы в секунду	Ноги	Слизняк	Slug foot quared
`English (Velocity in kts)`	Фунт	Фут-фунт	Футы в секунду за секунду	Узлы	Ноги	Слизняк	Slug foot quared

Программное использование

Параметры блоков: units

Тип: Вектор символов

Значения: Metric (MKS) | English (Velocity in ft/s) | English (Velocity in kts)

По умолчанию: Metric (MKS)

`Mass type` - Тип массы
`Fixed` (по умолчанию) | `Simple Variable` | `Custom Variable`

Выберите тип массы для использования:

Тип массы	Описание	По умолчанию для
`Fixed`	Масса постоянна на протяжении всей симуляции.	6DOF (Euler Angles) 6DOF (Quaternion) 6DOF Wind (Wind Angles) 6DOF Wind (Quaternion) 6DOF ECEF (Quaternion)
`Simple Variable`	Масса и инерция изменяются линейно как функция от массовой скорости.	Simple Variable Mass 6DOF (Euler Angles) Simple Variable Mass 6DOF (Quaternion) Simple Variable Mass 6DOF Wind (Wind Angles) Simple Variable Mass 6DOF Wind (Quaternion) Simple Variable Mass 6DOF ECEF (Quaternion)
`Custom Variable`	Изменения массы и инерции настраиваются.	Custom Variable Mass 6DOF (Euler Angles) Custom Variable Mass 6DOF (Quaternion) Custom Variable Mass 6DOF Wind (Wind Angles) Custom Variable Mass 6DOF Wind (Quaternion) Custom Variable Mass 6DOF ECEF (Quaternion)

The Fixed выбор соответствует описанным выше уравнениям движения.

Программное использование

Параметры блоков: mtype

Тип: Вектор символов

Значения: Fixed | Simple Variable | Custom Variable

По умолчанию: 'Simple Variable'

`Initial position in geodetic latitude, longitude and altitude [mu,l,h]` - Начальное расположение самолета
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальное расположение самолета в геодезической системе координат, заданное в виде трехэлементного вектора. Значения широты и долготы могут быть любым значением. Однако значения широты + 90 и -90 могут вернуть неожиданные значения из-за особенности на полюсах .

Программное использование

Параметры блоков: xg_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial velocity in body axes [U,v,w]` - Скорость в осях тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальная скорость в осях тела, заданная как трехэлементный вектор, в фиксированной в теле координатной системе координат.

Программное использование

Параметры блоков: Vm_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial Euler orientation [roll, pitch, yaw]` - Начальная ориентация Эйлера
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальные углы ориентации Эйлера [крен, тангаж, рыскание], заданные как трехэлементный вектор, в радианах. Углы поворота Эйлера являются углами между телом и северо-восточными-нисходящими (NED) системами координат.

Программное использование

Параметры блоков: eul_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial body rotation rates [p,q,r]` - Начальное вращение тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальные угловые скорости тела фиксированные относительно система координат, заданные как трехэлементный вектор, в радианах в секунду.

Программное использование

Параметры блоков: pm_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial mass` - Начальная масса
`1.0` (по умолчанию) | скаляром

Начальная масса твёрдого тела, заданная как двойной скаляр.

Программное использование

Параметры блоков: mass_0

Тип: Вектор символов

Значения: '1.0' | двойной скаляр

По умолчанию: '1.0'

`Inertia` - Инерция
`eye(3)` (по умолчанию) | скаляром

Инерция тела, заданная как двойной скаляр.

Зависимости

Чтобы включить этот параметр, установите Mass type равным Fixed.

Программное использование

Параметры блоков: inertia

Тип: Вектор символов

Значения: eye(3) | двойной скаляр

По умолчанию: eye(3)

`Include inertial acceleration` - Включите порт инерционного ускорения
`off` (по умолчанию) | `on`

Установите этот флажок, чтобы добавить инерционный порт ускорения.

Зависимости

Чтобы включить _Abe порт, выберите этот параметр.

Программное использование

Параметры блоков: abi_flag

Тип: Вектор символов

Значения: 'off' | 'on'

По умолчанию: off

Планета

`Planet model` - Модель планеты
`Earth (WGS84)` (по умолчанию) | `Custom`

Модель планеты для использования, Custom или Earth (WGS84).

Программное использование

Параметры блоков: ptype

Тип: Вектор символов

Значения: 'Earth (WGS84)' | 'Custom'

По умолчанию: 'Earth (WGS84)'

`Equatorial radius of planet` - Радиус планеты на экваторе
`6378137` (по умолчанию) | скаляром

Радиус планеты на ее экваторе, заданный как двойной скаляр, в тех же модулях измерения, что и требуемые модули для положения ECEF.

Зависимости

Чтобы включить этот параметр, установите Модель Планеты на Custom.

Программное использование

Параметры блоков: R

Тип: Вектор символов

Значения: двойной скаляр

По умолчанию: '6378137'

`Flattening` - Сплющивание планеты
`1/298.257223563` (по умолчанию) | скаляром

Уплощение планеты, заданное как двойной скаляр.

Зависимости

Чтобы включить этот параметр, установите Модель Планеты на Custom.

Программное использование

Параметры блоков: F

Тип: Вектор символов

Значения: двойной скаляр

По умолчанию: '1/298.257223563'

`Rotational rate` - Скорость вращения
`7292115e-11` (по умолчанию) | скаляром

Скорость вращения планеты, заданная как скаляр, в рад/с.

Зависимости

Чтобы включить этот параметр, установите Модель Планеты на Custom.

Программное использование

Параметры блоков: w_E

Тип: Вектор символов

Значения: двойной скаляр

По умолчанию: '7292115e-11'

`Celestial longitude of Greenwich source` - Источник исходной небесной долготы Гринвичского меридиана
`Internal` (по умолчанию) | `External`

Источник Гринвичской меридианской начальной небесной долготы, указанный как:

`Internal`	Используйте значение небесной долготы от Celestial longitude of Greenwich.
`External`	Используйте внешний вход для значения небесной долготы.

Зависимости

Установка этого параметра на External включает порт _LG(0).

Программное использование

Параметры блоков: angle_in

Тип: Вектор символов

Значения: 'Internal' | 'External'

По умолчанию: 'Internal'

`Celestial longitude of Greenwich [deg]` - Начальный угол
`0` (по умолчанию) | скаляром

Начальный угол между меридианом Гринвича и x-осью системы координат ECI, заданный как двойной скаляр.

Зависимости

Чтобы включить этот параметр, установите Celestial longitude of Greenwich source равным Internal.

Программное использование

Параметры блоков: LG0

Тип: Вектор символов

Значения: двойной скаляр

По умолчанию: '0'

Атрибуты состояния

Присвойте уникальное имя каждому состоянию. Можно использовать имена состояний вместо блока путей во время линеаризации.

Чтобы назначить имя одному состоянию, введите уникальное имя между кавычками, например 'velocity'.
Чтобы назначить имена нескольким состояниям, введите разделенный списками , разделенными запятыми, окруженный скобками, например {'a', 'b', 'c'}. Каждое имя должно быть уникальным.
Если параметр пуст (' '), имя не присвоено.
Имена состояний применяются только к выбранному блоку с параметром name.
Количество состояний должно разделяться равномерно между количеством имен состояний.
Можно задать меньше имен, чем состояний, но нельзя задать больше имен, чем состояний.
Для примера можно задать два имени в системе с четырьмя состояниями. Первое имя относится к первым двум состояниям, а второе - к последним двум состояниям.
Назначение имен состояний с переменной в MATLAB^® рабочая область, введите переменную без кавычек. Переменная может быть вектором символов, массивом ячеек или структурой.

`Quaternion vector: e.g., {'qr', 'qi', 'qj', 'qk'}` - Имя векторного состояния Кватерниона
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Имена состояний векторов кватерниона, заданные как разделенный списками , разделенными запятыми, окруженный скобками.

Программное использование

Параметры блоков: quat_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`Body rotation rates: e.g., {'p', 'q', 'r'}` - Имена состояний вращения тела
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Имена состояний скорости вращения тела, заданный разделенный списками , разделенными запятыми, окруженный скобками.

Программное использование

Параметры блоков: pm_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`Velocity: e.g., {'U', 'v', 'w'}` - имя состояния скорости
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Имена состояний скорости, заданные как разделенный списками , разделенными запятыми, окруженный скобками.

Программное использование

Параметры блоков: Vm_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`ECEF position: e.g., {'Xecef', 'Yecef', 'Zecef'}` - имя положения ECEF
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Названия состояния положения ECEF, заданные как список , разделенный запятыми, окруженная скобками.

Программное использование

Параметры блоков: posECEF_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`Inertial position: e.g., {'Xeci', 'Yeci', 'Zeci'}` - Имена состояний инерционной позиции
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Имена состояний инерционного положения, заданные как разделенный списками , разделенными запятыми, окруженный скобками.

Значение по умолчанию ''.

Программное использование

Параметры блоков: posECI_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`Celestial longitude of Greenwich: e.g., 'LG'` - имя состояния небесной долготы
`''` (по умолчанию) | вектор символов

Небесная долгота имени состояния Гринвича, заданная в виде вектора символов.

Программное использование

Параметры блоков: LG_statename

Тип: Вектор символов

Значения: '' | скаляр

По умолчанию: ''

Алгоритмы

Источником координатной системы координат ECEF является центр Земли. В сложение, тело интереса принято твердым, предположение, которое исключает необходимость рассматривать силы, действующие между отдельными элементами массы. Представление вращения системы координат ECEF из системы координат ECI упрощается, чтобы рассматривать только постоянное вращение эллипсоидной Земли (в e), включая начальную небесную долготу (_LG (0)). Это превосходное приближение позволяет пренебрегать силами, обусловленными комплексным движением Земли относительно «неподвижных звёзд».

Поступательное движение координатной системы координат ECEF приведено ниже, где приложенные силы [_{Fx Fy Fz}]^T находятся в каркасе кузова, и масса m тела принята постоянной.

${\bar{F}}_{b} = [\begin{matrix} F_{x} \\ F_{y} \\ F_{z} \end{matrix}] = m ({\dot{\bar{V}}}_{b} + {\bar{ω}}_{b} \times {\bar{V}}_{b} + D C M_{b f} {\bar{ω}}_{e} \times {\bar{V}}_{b} + D C M_{b f} ({\bar{ω}}_{e} \times ({\bar{ω}}_{e} \times {\bar{X}}_{f})))$

где изменение положения в ECEF ${\dot{\bar{x}}}_{f}$ вычисляется

${\dot{\bar{x}}}_{f} = D C M_{f b} {\bar{V}}_{b}$

и скорость тела относительно системы координат ECEF, выраженная в каркасе кузова $({\bar{V}}_{b})$ , угловые скорости тела относительно системы координат ECI, выраженные в каркасе кузова $({\bar{ω}}_{b})$ . Скорость вращения Земли $({\bar{ω}}_{e})$ , и относительные угловые скорости тела относительно северо-восточной-вниз (NED) системы координат, выраженные в каркасе кузова $({\bar{ω}}_{r e l})$ , определяются как

$\begin{array}{l} {\bar{V}}_{b} = [\begin{matrix} u \\ v \\ w \end{matrix}], {\bar{ω}}_{r e l} = [\begin{matrix} p \\ q \\ r \end{matrix}], {\bar{ω}}_{e} = [\begin{matrix} 0 \\ 0 \\ ω_{e} \end{matrix}], {\bar{ω}}_{b} = {\bar{ω}}_{r e l} + D C M_{b f} {\bar{ω}}_{e} + D C M_{b e} {\bar{ω}}_{n e d} \\ {\bar{ω}}_{n e d} = [\begin{matrix} \dot{l} \cos μ \\ - \dot{μ} \\ - \dot{l} \sin μ \end{matrix}] = [\begin{matrix} V_{E} / (N + h) \\ - V_{N} / (M + h) \\ - V_{E} • \tan μ / (N + h) \end{matrix}] \end{array}$

Динамика вращения тела, заданная в неподвижной системе координат тела, приведена ниже, где приложенные моменты [L M N]^T, и тензор инерции I относительно origin O.

$\begin{array}{l} A_{b b} = [\begin{matrix} {\dot{u}}_{b} \\ {\dot{v}}_{b} \\ {\dot{ω}}_{b} \end{matrix}] = \frac{1}{m} {\bar{F}}_{b} - [{\bar{ω}}_{b} \times {\bar{V}}_{b} + D C M_{b f} {\bar{ω}}_{e} \times {\bar{V}}_{b} + D C M_{b f} ({\bar{ω}}_{e} \times ({\bar{ω}}_{e} \times {\bar{X}}_{f}))] \\ A_{b} _{e c e f} = \frac{F_{b}}{m} \\ {\bar{M}}_{b} = [\begin{matrix} L \\ M \\ N \end{matrix}] = I {\dot{\bar{ω}}}_{b} + {\bar{ω}}_{b} \times (I {\bar{ω}}_{b}) \\ I = [\begin{matrix} I_{x x} & - I_{x y} & - I_{x z} \\ - I_{y x} & I_{y y} & - I_{y z} \\ - I_{z x} & - I_{z y} & I_{z z} \end{matrix}] \end{array}$

Интегрирование скорости изменения вектора кватерниона приведено ниже.

$[\begin{matrix} {\dot{q}}_{0} \\ {\dot{q}}_{1} \\ {\dot{q}}_{2} \\ {\dot{q}}_{3} \end{matrix}] = - \frac{1}{2} [\begin{matrix} 0 & ω_{b} (1) & ω_{b} (2) & ω_{b} (3) \\ - ω_{b} (1) & 0 & - ω_{b} (3) & ω_{b} (2) \\ - ω_{b} (2) & ω_{b} (3) & 0 & - ω_{b} (1) \\ - ω_{b} (3) & - ω_{b} (2) & ω_{b} (1) & 0 \end{matrix}] [\begin{matrix} q_{0} \\ q_{1} \\ q_{2} \\ q_{3} \end{matrix}]$

Аэрокосмическая Blockset™ использует кватернионы, которые заданы с помощью скалярно-первого соглашения.

Ссылки

[1] Стивенс, Брайан и Фрэнк Льюис. Aircraft Control and Simulation, 2nd ed. Hoboken, NJ: John Wiley & Sons, 2003.

[2] McFarland, Richard E. «Стандартная кинематическая модель для симуляции рейса в НАСА-Эймс». CR-2497 НАСА.

[3] «Дополнение к Всемирной геодезической системе министерства обороны 1984 года Технический доклад: Часть I - Методы, техники и данные, используемые в разработке WGS84». DMA- TR8350.2-A.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Введенный в R2006a

Документация

6DOF ECEF (Quaternion)

Описание

Ограничения

Порты

Вход

Fxyz - Приложенные силы трехэлементный вектор

Mxyz - Приложенные моменты трехэлементный вектор

LG(0) - Начальная небесная долгота Гринвича скаляр

Зависимости

Выход

Vecef - Скорость тела относительно системы координат ECEF, трехэлементный вектор

Xecef - Положение в системе координат ECEF трехэлементный вектор

μ l h - Положение в геодезической широте, долготе и высоте трехэлементный вектор | M-by-3 массив

φ θ Ψ (rad) - Углы поворота тела трехэлементный вектор

DCMbi - Преобразование координат из осей ECI Матрица 3 на 3

DCMbe - Преобразование координат из осей NED Матрица 3 на 3

DCMef - Преобразование координат из осей ECEF Матрица 3 на 3

Vb - Скорость тела относительно системы координат ECEF трехэлементный вектор

ωrel - Относительные угловые скорости тела относительно система координат трехэлементный вектор

ωb - Угловые скорости тела относительно системы координат ECI трехэлементный вектор

dωb/dt - Угловые ускорения корпуса относительно системы координат ECI трехэлементный вектор

Abb - Ускорения в неподвижных осях тела трехэлементный вектор

Ab ecef - Ускорения в неподвижных осях тела трехэлементный вектор

Зависимости

Параметры

Главный

Units - Входные и выходные модули Metric (MKS) (по умолчанию) | English (Velocity in ft/s) | English (Velocity in kts)

Программное использование

Mass type - Тип массы Fixed (по умолчанию) | Simple Variable | Custom Variable

Программное использование

Initial position in geodetic latitude, longitude and altitude [mu,l,h] - Начальное расположение самолета [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial velocity in body axes [U,v,w] - Скорость в осях тела [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial Euler orientation [roll, pitch, yaw] - Начальная ориентация Эйлера [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial body rotation rates [p,q,r] - Начальное вращение тела [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial mass - Начальная масса 1.0 (по умолчанию) | скаляром

Программное использование

Inertia - Инерция eye(3) (по умолчанию) | скаляром

Зависимости

Программное использование

Include inertial acceleration - Включите порт инерционного ускорения off (по умолчанию) | on

Зависимости

Программное использование

Планета

Planet model - Модель планеты Earth (WGS84) (по умолчанию) | Custom

Программное использование

Equatorial radius of planet - Радиус планеты на экваторе 6378137 (по умолчанию) | скаляром

Зависимости

Программное использование

Flattening - Сплющивание планеты 1/298.257223563 (по умолчанию) | скаляром

Зависимости

Программное использование

Rotational rate - Скорость вращения 7292115e-11 (по умолчанию) | скаляром

Зависимости

Программное использование

Celestial longitude of Greenwich source - Источник исходной небесной долготы Гринвичского меридиана Internal (по умолчанию) | External

Зависимости

Программное использование

Celestial longitude of Greenwich [deg] - Начальный угол 0 (по умолчанию) | скаляром

Зависимости

Программное использование

Атрибуты состояния

Quaternion vector: e.g., {'qr', 'qi', 'qj', 'qk'} - Имя векторного состояния Кватерниона '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Body rotation rates: e.g., {'p', 'q', 'r'} - Имена состояний вращения тела '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Velocity: e.g., {'U', 'v', 'w'} - имя состояния скорости '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

ECEF position: e.g., {'Xecef', 'Yecef', 'Zecef'} - имя положения ECEF '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Inertial position: e.g., {'Xeci', 'Yeci', 'Zeci'} - Имена состояний инерционной позиции '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Celestial longitude of Greenwich: e.g., 'LG' - имя состояния небесной долготы '' (по умолчанию) | вектор символов

Программное использование

Алгоритмы

Ссылки

`_Fxyz` - Приложенные силы
трехэлементный вектор

`_Mxyz` - Приложенные моменты
трехэлементный вектор

`_LG(0)` - Начальная небесная долгота Гринвича
скаляр

`_Vecef` - Скорость тела относительно системы координат ECEF,
трехэлементный вектор

`_Xecef` - Положение в системе координат ECEF
трехэлементный вектор

`μ l h` - Положение в геодезической широте, долготе и высоте
трехэлементный вектор | M-by-3 массив

`φ θ Ψ (rad)` - Углы поворота тела
трехэлементный вектор

`_DCMbi` - Преобразование координат из осей ECI
Матрица 3 на 3

`_DCMbe` - Преобразование координат из осей NED
Матрица 3 на 3

`_DCMef` - Преобразование координат из осей ECEF
Матрица 3 на 3

`_Vb` - Скорость тела относительно системы координат ECEF
трехэлементный вектор

`_ωrel` - Относительные угловые скорости тела относительно система координат
трехэлементный вектор

`_ωb` - Угловые скорости тела относительно системы координат ECI
трехэлементный вектор

`_dωb/dt` - Угловые ускорения корпуса относительно системы координат ECI
трехэлементный вектор

`_Abb` - Ускорения в неподвижных осях тела
трехэлементный вектор

`_{Ab ecef}` - Ускорения в неподвижных осях тела
трехэлементный вектор

`Units` - Входные и выходные модули
`Metric (MKS)` (по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

`Mass type` - Тип массы
`Fixed` (по умолчанию) | `Simple Variable` | `Custom Variable`

`Initial position in geodetic latitude, longitude and altitude [mu,l,h]` - Начальное расположение самолета
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial velocity in body axes [U,v,w]` - Скорость в осях тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial Euler orientation [roll, pitch, yaw]` - Начальная ориентация Эйлера
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial body rotation rates [p,q,r]` - Начальное вращение тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial mass` - Начальная масса
`1.0` (по умолчанию) | скаляром

`Inertia` - Инерция
`eye(3)` (по умолчанию) | скаляром

`Include inertial acceleration` - Включите порт инерционного ускорения
`off` (по умолчанию) | `on`

`Planet model` - Модель планеты
`Earth (WGS84)` (по умолчанию) | `Custom`

`Equatorial radius of planet` - Радиус планеты на экваторе
`6378137` (по умолчанию) | скаляром

`Flattening` - Сплющивание планеты
`1/298.257223563` (по умолчанию) | скаляром

`Rotational rate` - Скорость вращения
`7292115e-11` (по умолчанию) | скаляром

`Celestial longitude of Greenwich source` - Источник исходной небесной долготы Гринвичского меридиана
`Internal` (по умолчанию) | `External`

`Celestial longitude of Greenwich [deg]` - Начальный угол
`0` (по умолчанию) | скаляром

`Quaternion vector: e.g., {'qr', 'qi', 'qj', 'qk'}` - Имя векторного состояния Кватерниона
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`Body rotation rates: e.g., {'p', 'q', 'r'}` - Имена состояний вращения тела
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`Velocity: e.g., {'U', 'v', 'w'}` - имя состояния скорости
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`ECEF position: e.g., {'Xecef', 'Yecef', 'Zecef'}` - имя положения ECEF
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`Inertial position: e.g., {'Xeci', 'Yeci', 'Zeci'}` - Имена состояний инерционной позиции
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`Celestial longitude of Greenwich: e.g., 'LG'` - имя состояния небесной долготы
`''` (по умолчанию) | вектор символов

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®