6DOF (Euler Angles)

Реализуйте представление угла Эйлера уравнений движения с шестью степенями свободы

Библиотека:
Аэрокосмический Уравнения Движения/ 6DOF

Описание

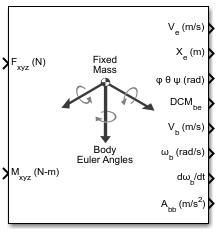
Блок 6DOF (Euler Angles) реализует представление угла Эйлера уравнений движения с шестью степенями свободы, принимая во внимание вращение неподвижной координатной системы координат (_{Xb, Yb, Zb}) вокруг плоской системы отсчета Земли (_{Xe, Ye, Ze}). Для получения дополнительной информации об этих ссылочных точках см. «Алгоритмы».

Ограничения

Блок принимает, что приложенные силы действуют в центре тяжести тела, и что масса и инерция постоянны.

Порты

Вход

расширить все

`_Fxyz(N)` - Приложенные силы
трехэлементный вектор

Приложенные силы, заданные как трехэлементный вектор.

Типы данных: double

`_Mxyz(N-m)` - Приложенные моменты
трехэлементный вектор

Приложенные моменты, заданные как трехэлементный вектор.

Типы данных: double

Выход

расширить все

`_Ve` - Скорость в плоской системе отсчета Земли
трехэлементный вектор

Скорость в плоской земной системе координат, возвращенная как трехэлементный вектор.

Типы данных: double

`_Xe` - Положение в плоской системе отсчета Земли
трехэлементный вектор

Положение в плоской системе координат Земли, возвращаемое как трехэлементный вектор.

Типы данных: double

`φ θ ψ (rad)` - углы поворота Эйлера
трехэлементный вектор

Углы поворота Эйлера [крен, тангаж, рыскание], возвращаемые в виде трехэлементного вектора, в радианах.

Типы данных: double

`_DCMbe` - Преобразование координат
Матрица 3 на 3

Координатное преобразование от плоских осей Земли к фиксированным осям тела, возвращаемое как матрица 3 на 3.

Типы данных: double

`_Vb` - Скорость в неподвижной системе координат тела
трехэлементный вектор

Скорость в фиксированной по телу системе координат, возвращаемая как трехэлементный вектор.

Типы данных: double

`_{ωb (rad/s)}` - Угловые скорости в фиксированных осях тела
трехэлементный вектор

Угловые скорости в фиксированных осях тела, возвращаемые как трехэлементный вектор, в радианах в секунду.

Типы данных: double

`_dωb/dt` - Угловое ускорение
трехэлементный вектор

Угловые ускорения в фиксированных по телу осях, возвращаемые как трехэлементный вектор, в радианах в секунду за секунду.

Типы данных: double

`_Abb` - Ускорения в неподвижных осях тела
трехэлементный вектор

Ускорения в неподвижных осях тела относительно каркаса кузова, возвращаемые как трехэлементный вектор.

Типы данных: double

`_Abe` - Ускорения относительно инерционной системы координат
трехэлементный вектор

Ускорения в фиксированных по телу осях относительно инерционной системы координат (плоская Земля), возвращаемые как трехэлементный вектор. Обычно вы соединяете этот сигнал с акселерометром.

Зависимости

Этот порт появляется только при установке флажка Include inertial acceleration.

Типы данных: double

Параметры

расширить все

Главный

`Units` - Входные и выходные модули
`Metric (MKS)` (по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

Входной и выходной модули, заданные как Metric (MKS), English (Velocity in ft/s), или English (Velocity in kts).

Модули	Силы	Момент	Ускорение	Скорость	Положение	Масса	Инерция
`Metric (MKS)`	Ньютон	Ньютон-метр	Метры в секунду за секунду	Метры в секунду	Метры	Килограмм	Килограмм-метр в квадрате
`English (Velocity in ft/s)`	Фунт	Фут-фунт	Футы в секунду за секунду	Футы в секунду	Ноги	Слизняк	Slug foot quared
`English (Velocity in kts)`	Фунт	Фут-фунт	Футы в секунду за секунду	Узлы	Ноги	Слизняк	Slug foot quared

Программное использование

Параметры блоков: units

Тип: Вектор символов

Значения: Metric (MKS) | English (Velocity in ft/s) | English (Velocity in kts)

По умолчанию: Metric (MKS)

`Mass Type` - Тип массы
`Fixed` (по умолчанию) | `Simple Variable` | `Custom Variable`

Тип массы, заданный согласно следующей таблице.

Тип массы	Описание	По умолчанию для
`Fixed`	Масса постоянна на протяжении всей симуляции.	6DOF (Euler Angles) 6DOF (Quaternion) 6DOF Wind (Wind Angles) 6DOF Wind (Quaternion) 6DOF ECEF (Quaternion)
`Simple Variable`	Масса и инерция изменяются линейно как функция от массовой скорости.	Simple Variable Mass 6DOF (Euler Angles) Simple Variable Mass 6DOF (Quaternion) Simple Variable Mass 6DOF Wind (Wind Angles) Simple Variable Mass 6DOF Wind (Quaternion) Simple Variable Mass 6DOF ECEF (Quaternion)
`Custom Variable`	Изменения массы и инерции настраиваются.	Custom Variable Mass 6DOF (Euler Angles) Custom Variable Mass 6DOF (Quaternion) Custom Variable Mass 6DOF Wind (Wind Angles) Custom Variable Mass 6DOF Wind (Quaternion) Custom Variable Mass 6DOF ECEF (Quaternion)

The Simple Variable выбор соответствует описанным выше уравнениям движения.

Программное использование

Параметры блоков: mtype

Тип: Вектор символов

Значения: Fixed | Simple Variable | Custom Variable

По умолчанию: Simple Variable

`Representation` - Уравнения представления движения
`Euler Angles` (по умолчанию) | `Quaternion`

Уравнения представления движения, заданные согласно следующей таблице.

Представление	Описание
`Euler Angles`	Используйте углы Эйлера в уравнениях движения.
`Quaternion`	Используйте кватернионы в уравнениях движения.

The Quaternion выбор соответствует уравнениям движения в Алгоритмах.

Программное использование

Параметры блоков: rep

Тип: Вектор символов

Значения: Euler Angles | Quaternion

По умолчанию: 'Euler Angles'

`Initial position in inertial axes [Xe,Ye,Ze]` - Положение в инерционных осях
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальное расположение тела в плоской земной системе координат, заданное как трехэлементный вектор.

Программное использование

Параметры блоков: xme_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial velocity in body axes [U,v,w]` - Скорость в осях тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальная скорость в осях тела, заданная как трехэлементный вектор, в фиксированной в теле координатной системе координат.

Программное использование

Параметры блоков: Vm_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial Euler orientation [roll, pitch, yaw]` - Начальная ориентация Эйлера
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальные углы ориентации Эйлера [крен, тангаж, рыскание], заданные как трехэлементный вектор, в радианах. Углы поворота Эйлера являются углами между телом и северо-восточными-нисходящими (NED) системами координат.

Программное использование

Параметры блоков: eul_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial body rotation rates [p,q,r]` - Начальное вращение тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

Начальные угловые скорости тела фиксированные относительно система координат, заданные как трехэлементный вектор, в радианах в секунду.

Программное использование

Параметры блоков: pm_0

Тип: Вектор символов

Значения: '[0 0 0]' | трехэлементный вектор

По умолчанию: '[0 0 0]'

`Initial mass` - Начальная масса
`1.0` (по умолчанию) | скаляром

Начальная масса твёрдого тела, заданная как двойной скаляр.

Программное использование

Параметры блоков: mass_0

Тип: Вектор символов

Значения: '1.0' | двойной скаляр

По умолчанию: '1.0'

`Inertia` - Инерция
`eye(3)` (по умолчанию) | скаляром

Инерция тела, заданная как двойной скаляр.

Зависимости

Чтобы включить этот параметр, установите Mass type равным Fixed.

Программное использование

Параметры блоков: inertia

Тип: Вектор символов

Значения: eye(3) | двойной скаляр

По умолчанию: eye(3)

`Include inertial acceleration` - Включите порт инерционного ускорения
`off` (по умолчанию) | `on`

Установите этот флажок, чтобы добавить инерционный порт ускорения.

Зависимости

Чтобы включить _Abe порт, выберите этот параметр.

Программное использование

Параметры блоков: abi_flag

Тип: Вектор символов

Значения: 'off' | 'on'

По умолчанию: off

Атрибуты состояния

Присвойте уникальное имя каждому состоянию. Можно использовать имена состояний вместо блока путей во время линеаризации.

Чтобы назначить имя одному состоянию, введите уникальное имя между кавычками, например 'velocity'.
Чтобы назначить имена нескольким состояниям, введите список с разделителем запятыми, окруженный скобками, например {'a', 'b', 'c'}. Каждое имя должно быть уникальным.
Если параметр пуст (' '), присвоение имен не происходит.
Имена состояний применяются только к выбранному блоку с параметром name.
Количество состояний должно разделяться равномерно между количеством имен состояний.
Можно задать меньше имен, чем состояний, но нельзя задать больше имен, чем состояний.
Для примера можно задать два имени в системе с четырьмя состояниями. Первое имя относится к первым двум состояниям, а второе - к последним двум состояниям.
Назначение имен состояний с переменной в MATLAB^® рабочая область, введите переменную без кавычек. Переменная может быть вектором символов, массивом ячеек или структурой.

`Position: e.g., {'Xe', 'Ye', 'Ze'}` - имя состояния положения
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Позиционные имена состояний, заданные как разделенный списками , разделенными запятыми, окруженный скобками.

Программное использование

Параметры блоков: xme_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`Velocity: e.g., {'U', 'v', 'w'}` - имя состояния скорости
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Имена состояний скорости, заданные как разделенный списками , разделенными запятыми, окруженный скобками.

Программное использование

Параметры блоков: Vm_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`Euler rotation angles: e.g., {'phi', 'theta', 'psi'}` - имя состояния вращения Эйлера
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Имена состояний угла поворота Эйлера, заданные как разделенный списками , разделенными запятыми, окруженный скобками.

Программное использование

Параметры блоков: eul_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

`Body rotation rates: e.g., {'p', 'q', 'r'}` - Имена состояний вращения тела
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Имена состояний скорости вращения тела, заданный разделенный списками , разделенными запятыми, окруженный скобками.

Программное использование

Параметры блоков: pm_statename

Тип: Вектор символов

Значения: '' | разделенный запятыми список, окруженный скобками

По умолчанию: ''

Алгоритмы

Блок 6DOF (Euler Angles) использует эти концепции систем координат.

Источником координатной системы координат тела является центр тяжести тела, и тело принято твердым, что исключает необходимость рассматривать силы, действующие между отдельными элементами массы.
Плоская система координат Земли считается инерционной, отличное приближение, которое позволяет пренебрегать силами, обусловленными движением Земли относительно «неподвижных звёзд».
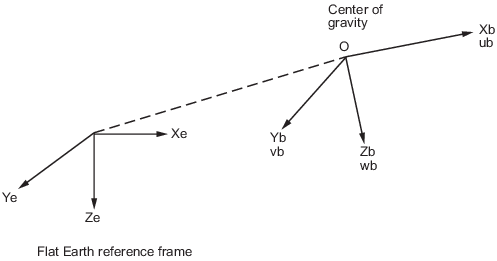
Поступательное движение неподвижной координатной системы координат, где приложенные силы [_{Fx Fy Fz}]^T находятся в фиксированной по телу системе координат, и масса m тела принята постоянной.
$\begin{array}{l} {\bar{F}}_{b} = [\begin{matrix} F_{x} \\ F_{y} \\ F_{z} \end{matrix}] = m ({\dot{\bar{V}}}_{b} + \bar{ω} \times {\bar{V}}_{b}) \\ A_{b b} = [\begin{matrix} {\dot{u}}_{b} \\ {\dot{v}}_{b} \\ {\dot{w}}_{b} \end{matrix}] = \frac{1}{m} {\bar{F}}_{b} - \bar{ω} \times {\bar{V}}_{b} \\ A_{b e} = \frac{1}{m} F_{b} \\ {\bar{V}}_{b} = [\begin{matrix} u_{b} \\ v_{b} \\ w_{b} \end{matrix}], \bar{ω} = [\begin{matrix} p \\ q \\ r \end{matrix}] \end{array}$
Динамика вращения неподвижной системы координат, где приложенные моменты [L M N]^T, и тензор инерции I относительно origin O.
$\begin{array}{l} {\bar{M}}_{B} = [\begin{matrix} L \\ M \\ N \end{matrix}] = I \dot{\bar{ω}} + \bar{ω} \times (I \bar{ω}) \\ I = [\begin{matrix} I_{x x} & - I_{x y} & - I_{x z} \\ - I_{y x} & I_{y y} & - I_{y z} \\ - I_{z x} & - I_{z y} & I_{z z} \end{matrix}] \end{array}$
Отношение между вектором скорости вращения с фиксированным телом, [p q r]^Tи скорость изменения углов Эйлера, $[\begin{matrix} \dot{ϕ} & \dot{θ} & \dot{ψ} \end{matrix}]^{T}$ , определяются путем разрешения скоростей Эйлера в фиксированную в теле координатную систему координат.
$[\begin{matrix} p \\ q \\ r \end{matrix}] = [\begin{matrix} \dot{ϕ} \\ 0 \\ 0 \end{matrix}] + [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos ϕ & \sin ϕ \\ 0 & - \sin ϕ & \cos ϕ \end{matrix}] [\begin{matrix} 0 \\ \dot{θ} \\ 0 \end{matrix}] + [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos ϕ & \sin ϕ \\ 0 & - \sin ϕ & \cos ϕ \end{matrix}] [\begin{matrix} \cos θ & 0 & - \sin θ \\ 0 & 1 & 0 \\ \sin θ & 0 & \cos θ \end{matrix}] [\begin{matrix} 0 \\ 0 \\ \dot{ψ} \end{matrix}] \equiv J^{- 1} [\begin{matrix} \dot{ϕ} \\ \dot{θ} \\ \dot{ψ} \end{matrix}]$
Инвертирование J затем дает необходимую зависимость, чтобы определить вектор скорости Эйлера.
$[\begin{matrix} \dot{ϕ} \\ \dot{θ} \\ \dot{ψ} \end{matrix}] = J [\begin{matrix} p \\ q \\ r \end{matrix}] = [\begin{matrix} 1 & (\sin ϕ \tan θ) & (\cos ϕ \tan θ) \\ 0 & \cos ϕ & - \sin ϕ \\ 0 & \frac{\sin ϕ}{\cos θ} & \frac{\cos ϕ}{\cos θ} \end{matrix}] [\begin{matrix} p \\ q \\ r \end{matrix}]$

Ссылки

[1] Стивенс, Брайан и Фрэнк Льюис, Aircraft Control and Simulation. Hoboken, NJ: Second Edition, John Wiley & Sons, 2003.

[2] Zipfel, Peter H., Моделирование и симуляция аэрокосмической Динамики аппарата. Reston, Va: Second Edition, AIAA Education Series, 2007.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Темы

Сведения о аэрокосмических системах координат

Введенный в R2006a

Документация

6DOF (Euler Angles)

Описание

Ограничения

Порты

Вход

Fxyz(N) - Приложенные силы трехэлементный вектор

Mxyz(N-m) - Приложенные моменты трехэлементный вектор

Выход

Ve - Скорость в плоской системе отсчета Земли трехэлементный вектор

Xe - Положение в плоской системе отсчета Земли трехэлементный вектор

φ θ ψ (rad) - углы поворота Эйлера трехэлементный вектор

DCMbe - Преобразование координат Матрица 3 на 3

Vb - Скорость в неподвижной системе координат тела трехэлементный вектор

ωb (rad/s) - Угловые скорости в фиксированных осях тела трехэлементный вектор

dωb/dt - Угловое ускорение трехэлементный вектор

Abb - Ускорения в неподвижных осях тела трехэлементный вектор

Abe - Ускорения относительно инерционной системы координат трехэлементный вектор

Зависимости

Параметры

Главный

Units - Входные и выходные модули Metric (MKS) (по умолчанию) | English (Velocity in ft/s) | English (Velocity in kts)

Программное использование

Mass Type - Тип массы Fixed (по умолчанию) | Simple Variable | Custom Variable

Программное использование

Representation - Уравнения представления движения Euler Angles (по умолчанию) | Quaternion

Программное использование

Initial position in inertial axes [Xe,Ye,Ze] - Положение в инерционных осях [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial velocity in body axes [U,v,w] - Скорость в осях тела [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial Euler orientation [roll, pitch, yaw] - Начальная ориентация Эйлера [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial body rotation rates [p,q,r] - Начальное вращение тела [0 0 0] (по умолчанию) | трехэлементный вектор

Программное использование

Initial mass - Начальная масса 1.0 (по умолчанию) | скаляром

Программное использование

Inertia - Инерция eye(3) (по умолчанию) | скаляром

Зависимости

Программное использование

Include inertial acceleration - Включите порт инерционного ускорения off (по умолчанию) | on

Зависимости

Программное использование

Атрибуты состояния

Position: e.g., {'Xe', 'Ye', 'Ze'} - имя состояния положения '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Velocity: e.g., {'U', 'v', 'w'} - имя состояния скорости '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Euler rotation angles: e.g., {'phi', 'theta', 'psi'} - имя состояния вращения Эйлера '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Body rotation rates: e.g., {'p', 'q', 'r'} - Имена состояний вращения тела '' (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Программное использование

Алгоритмы

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Темы

Документация Aerospace Blockset

Поддержка

`_Fxyz(N)` - Приложенные силы
трехэлементный вектор

`_Mxyz(N-m)` - Приложенные моменты
трехэлементный вектор

`_Ve` - Скорость в плоской системе отсчета Земли
трехэлементный вектор

`_Xe` - Положение в плоской системе отсчета Земли
трехэлементный вектор

`φ θ ψ (rad)` - углы поворота Эйлера
трехэлементный вектор

`_DCMbe` - Преобразование координат
Матрица 3 на 3

`_Vb` - Скорость в неподвижной системе координат тела
трехэлементный вектор

`_{ωb (rad/s)}` - Угловые скорости в фиксированных осях тела
трехэлементный вектор

`_dωb/dt` - Угловое ускорение
трехэлементный вектор

`_Abb` - Ускорения в неподвижных осях тела
трехэлементный вектор

`_Abe` - Ускорения относительно инерционной системы координат
трехэлементный вектор

`Units` - Входные и выходные модули
`Metric (MKS)` (по умолчанию) | `English (Velocity in ft/s)` | `English (Velocity in kts)`

`Mass Type` - Тип массы
`Fixed` (по умолчанию) | `Simple Variable` | `Custom Variable`

`Representation` - Уравнения представления движения
`Euler Angles` (по умолчанию) | `Quaternion`

`Initial position in inertial axes [Xe,Ye,Ze]` - Положение в инерционных осях
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial velocity in body axes [U,v,w]` - Скорость в осях тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial Euler orientation [roll, pitch, yaw]` - Начальная ориентация Эйлера
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial body rotation rates [p,q,r]` - Начальное вращение тела
`[0 0 0]` (по умолчанию) | трехэлементный вектор

`Initial mass` - Начальная масса
`1.0` (по умолчанию) | скаляром

`Inertia` - Инерция
`eye(3)` (по умолчанию) | скаляром

`Include inertial acceleration` - Включите порт инерционного ускорения
`off` (по умолчанию) | `on`

`Position: e.g., {'Xe', 'Ye', 'Ze'}` - имя состояния положения
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`Velocity: e.g., {'U', 'v', 'w'}` - имя состояния скорости
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`Euler rotation angles: e.g., {'phi', 'theta', 'psi'}` - имя состояния вращения Эйлера
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

`Body rotation rates: e.g., {'p', 'q', 'r'}` - Имена состояний вращения тела
`''` (по умолчанию) | разделенный списками , разделенными запятыми, окруженный скобками

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®