graphconncomp

Найдите сильно или слабо связанные компоненты в графике

Синтаксис

[S, C] = graphconncomp(G) [S, C] = graphconncomp(G, ...'Directed', DirectedValue, ...) [S, C] = graphconncomp(G, ...'Weak', WeakValue, ...)

Аргументы

`G`	N-на-N разреженная матрица, которая представляет график. Ненулевые значения в матричных `G` указать наличие ребра.
`DirectedValue`	Свойство, которое указывает, направлен ли график или не направлен. Введите `false` для неориентированного графа. Это приводит к игнорированию верхнего треугольника разреженной матрицы. По умолчанию это `true`. Алгоритм на основе DFS вычисляет подключенные компоненты. Сложность во времени `O(N+E)`, где `N` и `E` являются числом узлов и кромками соответственно.
`WeakValue`	Свойство, которое указывает, находить ли слабо соединенные компоненты или сильно соединенные компоненты. Слабо связанный компонент является максимальной группой узлов, которые взаимно достижимы путем нарушения краевых направлений. Задайте `WeakValue` на `true` для поиска слабо связанных компонентов. По умолчанию это `false`, который находит сильно связанные компоненты. Состояние этого параметра не влияет на неориентированные графы, потому что слабо и сильно связанные компоненты одинаковы в неориентированных графах. Сложность во времени `O(N+E)`, где `N` и `E` являются числом узлов и кромками соответственно.

Описание

Совет

Для получения вводной информации о функциях теории графиков, см. «Функции теории графиков».

[S, C] = graphconncomp(G) находит сильно связанные компоненты графика, представленные матрицей G использование алгоритма Тарьяна. Сильно связанный компонент является максимальной группой узлов, которые взаимно достижимы, не нарушая краевых направлений. Входные G является N-на-N разреженной матрицей, которая представляет график. Ненулевые значения в матричных G указать наличие ребра.

Количество найденных компонентов возвращается в S, и C - вектор, указывающий, к какому компоненту принадлежит каждый узел.

Алгоритм Тарьяна имеет временную сложность O(N+E), где N и E являются числом узлов и кромками соответственно.

[S, C] = graphconncomp (G... 'PropertyName', PropertyValue, ...) вызывает graphconncomp с необязательными свойствами, которые используют пары имя/значение свойства. Можно задать одно или несколько свойств в любом порядке. Каждый PropertyName должны быть заключены в одинарные кавычки и нечувствительны к регистру. Эти имена свойства/пары значения свойств следующие:

[S, C] = graphconncomp(G, ...'Directed', DirectedValue, ...) указывает, направлен ли график или не направлен. Задайте directedValue на false для неориентированного графа. Это приводит к игнорированию верхнего треугольника разреженной матрицы. По умолчанию это true. Алгоритм на основе DFS вычисляет подключенные компоненты. Сложность во времени O(N+E), где N и E являются числом узлов и кромками соответственно.

[S, C] = graphconncomp(G, ...'Weak', WeakValue, ...) указывает, нужно ли находить слабо соединенные компоненты или сильно соединенные компоненты. Слабо связанный компонент является максимальной группой узлов, которые взаимно достижимы путем нарушения краевых направлений. Задайте WeakValue на true для поиска слабо связанных компонентов. По умолчанию это false, который находит сильно связанные компоненты. Состояние этого параметра не влияет на неориентированные графы, потому что слабо и сильно связанные компоненты одинаковы в неориентированных графах. Сложность во времени O(N+E), где N и E являются числом узлов и кромками соответственно.

Примечание

По определению, один узел может быть тесно связанным компонентом.

Примечание

Ориентированный ациклический график (DAG) не может иметь каких-либо сильно связанных компонентов, больше единицы.

Примеры

Создайте и просмотрите ориентированный график с 10 узлами и 17 ребрами.

DG = sparse([1 1 1 2 2 3 3 4 5 6 7 7 8 9 9  9 9], ...
           [2 6 8 3 1 4 2 5 4 7 6 4 9 8 10 5 3],true,10,10)

DG =

   (2,1)        1
   (1,2)        1
   (3,2)        1
   (2,3)        1
   (9,3)        1
   (3,4)        1
   (5,4)        1
   (7,4)        1
   (4,5)        1
   (9,5)        1
   (1,6)        1
   (7,6)        1
   (6,7)        1
   (1,8)        1
   (9,8)        1
   (8,9)        1
   (9,10)       1

h = view(biograph(DG));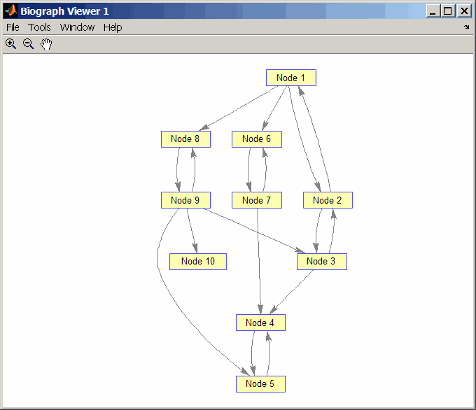

Найдите количество сильно связанных компонентов в ориентированном графе и определите, к какому компоненту принадлежит каждый из 10 узлов.
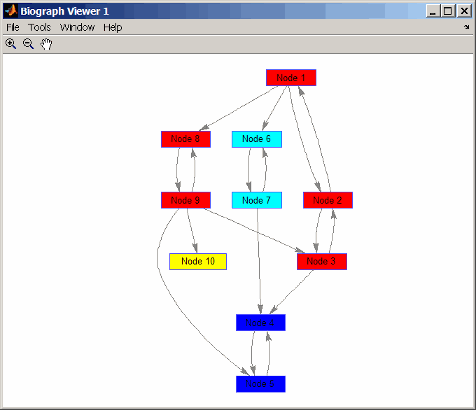
```
[S,C] = graphconncomp(DG)

S =

     4


C =

     4     4     4     1     1     2     2     4     4     3
```
Окрашивайте узлы для каждого компонента другим цветом.
```
colors = jet(S);
for i = 1:numel(h.nodes)
  h.Nodes(i).Color = colors(C(i),:);
end
```

Ссылки

[1] Тарьян, Р.Э., (1972). Глубина первого поиска и алгоритмы линейного графика. SIAM Journal on Computing 1 (2), 146-160.

[2] Sedgewick, R., (2002). Алгоритмы в C++, Алгоритмы графика части 5 (Эддисон-Уэсли).

[3] Siek, J.G., Lee, L-Q, and Lumsdaine, A. (2002). Руководство пользователя библиотеки График (Upper Saddle River, NJ: Pearson Education).

См. также

Документация