graphtraverse

График Траверса путем следования за смежными узлами

Синтаксис

[disc, pred, closed] = graphtraverse(G, S) [...] = graphtraverse(G, S, ...'Depth', DepthValue, ...) [...] = graphtraverse(G, S, ...'Directed', DirectedValue, ...) [...] = graphtraverse(G, S, ...'Method', MethodValue, ...)

Аргументы

`G`	N-на-N разреженная матрица, которая представляет ориентированный граф. Ненулевые значения в матричных `G` указать наличие ребра.
`S`	Целое число, которое указывает исходный узел в графике `G`.
`DepthValue`	Целое число, которое указывает узел в графике `G` , задающий глубину поиска. По умолчанию это `Inf` (бесконечность).
`DirectedValue`	Свойство, которое указывает, `G` ли графиков направлен или неориентирован. Введите `false` для неориентированного графа. Это приводит к игнорированию верхнего треугольника разреженной матрицы. По умолчанию это `true`.
`MethodValue`	Вектор символов, которая задает алгоритм, используемый для прохождения графика. Варианты: `'BFS'` - Широта - первый поиск. Сложность во времени `O(N+E)`, где `N` и `E` являются числом узлов и кромками соответственно. `'DFS'` - Алгоритм по умолчанию. Поиск глубины - первый. Сложность во времени `O(N+E)`, где `N` и `E` являются числом узлов и кромками соответственно.

Описание

Совет

Для получения вводной информации о функциях теории графиков, см. «Функции теории графиков».

[disc, pred, closed] = graphtraverse(G, S) идёт по графику G начиная с узла, обозначенного целым числом S. G является N-на-N разреженной матрицей, которая представляет ориентированный граф. Ненулевые значения в матричных G указать наличие ребра. disc является вектором индексов узлов в том порядке, в котором они обнаружены. pred является вектором индексов предшествующих узлов (перечисленных в порядке индексов узлов) получившегося покрывающего дерева. closed является вектором индексов узлов в том порядке, в котором они закрыты.

[...] = графтравра (G, S ... 'PropertyName', PropertyValue, ...) вызывает graphtraverse с необязательными свойствами, которые используют пары имя/значение свойства. Можно задать одно или несколько свойств в любом порядке. Каждый PropertyName должны быть заключены в одинарные кавычки и нечувствительны к регистру. Эти имена свойства/пары значения свойств следующие:

[...] = graphtraverse(G, S, ...'Depth', DepthValue, ...) задает глубину поиска. DepthValue - целое число, указывающее узел в графике G. По умолчанию это Inf (бесконечность).

[...] = graphtraverse(G, S, ...'Directed', DirectedValue, ...) указывает, направлен ли график или не направлен. Задайте DirectedValue на false для неориентированного графа. Это приводит к игнорированию верхнего треугольника разреженной матрицы. По умолчанию это true.

[...] = graphtraverse(G, S, ...'Method', MethodValue, ...) позволяет вам задать алгоритм, используемый для прохождения графика. Варианты:

'BFS' - Широта - первый поиск. Сложность во времени O(N+E), где N и E являются числом узлов и кромками соответственно.
'DFS' - Алгоритм по умолчанию. Поиск глубины - первый. Сложность во времени O(N+E), где N и E являются числом узлов и кромками соответственно.

Примеры

Создайте ориентированный граф с 10 узлами и 12 ребрами.

DG = sparse([1 2 3 4 5 5 5 6 7 8 8 9],...
              [2 4 1 5 3 6 7 9 8 1 10 2],true,10,10)

DG =

   (3,1)        1
   (8,1)        1
   (1,2)        1
   (9,2)        1
   (5,3)        1
   (2,4)        1
   (4,5)        1
   (5,6)        1
   (5,7)        1
   (7,8)        1
   (6,9)        1
   (8,10)       1

h = view(biograph(DG))
Biograph object with 10 nodes and 12 edges.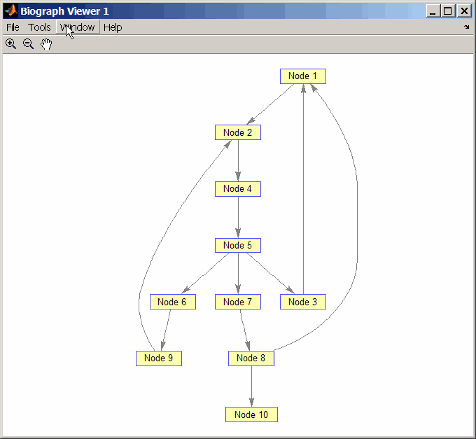

Пройдите по графику, чтобы найти порядок обнаружения первого поиска глубины (DFS), начиная с узла 4.
```
order = graphtraverse(DG,4)

order =

     4     5     3     1     2     6     9     7     8    10
```

Пометьте узлы порядком обнаружения DFS.

for i = 1:10
    h.Nodes(order(i)).Label =...
			sprintf('%s:%d',h.Nodes(order(i)).ID,i);
end
h.ShowTextInNodes = 'label'
dolayout(h)

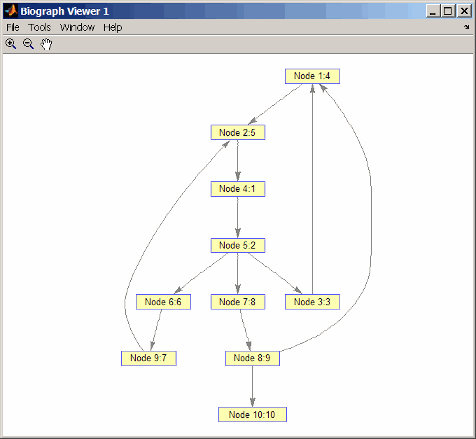
Пройдите по графику, чтобы найти порядок обнаружения первого поиска ширины (BFS), начиная с узла 4.
```
order = graphtraverse(DG,4,'Method','BFS')

order =

     4     5     3     6     7     1     9     8     2    10
```

Пометьте узлы порядком обнаружения BFS.

for i = 1:10
    h.Nodes(order(i)).Label =...
			sprintf('%s:%d',h.Nodes(order(i)).ID,i);
end
h.ShowTextInNodes = 'label'
dolayout(h)

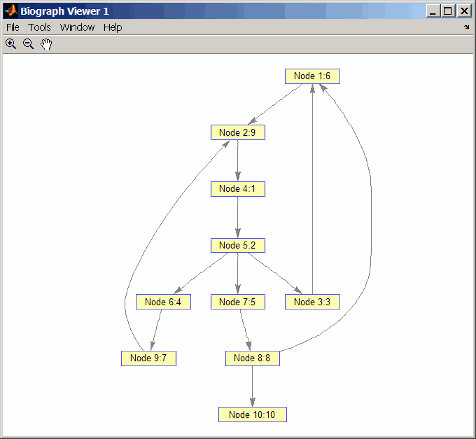
Поиск и цветовые узлы, которые близки (в пределах двух ребер) узлу 4.

node_idxs = graphtraverse(DG,4,'depth',2)

node_idxs =

     4     5     3     6     7

set(h.nodes(node_idxs),'Color',[1 0 0])

Ссылки

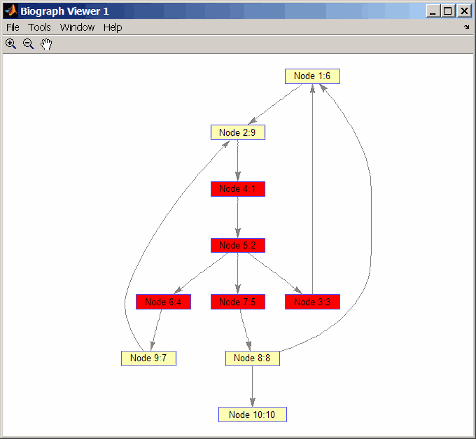
[1] Sedgewick, R., (2002). Алгоритмы в C++, Алгоритмы графика части 5 (Эддисон-Уэсли).

[2] Siek, J.G., Lee, L-Q, and Lumsdaine, A. (2002). Руководство пользователя библиотеки График (Upper Saddle River, NJ: Pearson Education).

См. также

Введенный в R2006b

Документация