graphisomorphism

Найдите изоморфизм между двумя графиками

Синтаксис

[Isomorphic, Map] = graphisomorphism(G1, G2) [Isomorphic, Map] = graphisomorphism(G1, G2,'Directed', DirectedValue)

Аргументы

`G1`	N-на-N разреженная матрица, которая представляет направленный или неориентированный граф. Ненулевые значения в матричных `G1` указать наличие ребра.
`G2`	N-на-N разреженная матрица, которая представляет направленный или неориентированный граф. `G2` должны быть такими же (направленными или неориентированными), как `G1`.
`DirectedValue`	Свойство, которое указывает, направлены ли графики или не направлены. Введите `false` когда оба `G1` и `G2` являются неориентированными графами. В этом случае верхние треугольники разреженных матриц `G1` и `G2` игнорируются. По умолчанию это `true`, что означает, что оба графиков направлены.

Описание

Совет

Для получения вводной информации о функциях теории графиков, см. «Функции теории графиков».

[Isomorphic, Map] = graphisomorphism(G1, G2) возвращает логический 1 (true) в Isomorphic если G1 и G2 являются изоморфными графиками и логическими 0 (false) в противном случае. Изоморфизм графика является отображением узлов в графике с 1 по 1 G1 и узлы в графике G2 таким образом, что смежности сохраняются. G1 и G2 являются обеими N-на-N разреженными матрицами, которые представляют ориентированные или неориентированные графы. Возвращаемое значение Isomorphic является логическим. Когда Isomorphic является true, Map - вектор-строка, содержащая индексы узлов, которые сопоставлены с G2 на G1 для одного возможного изоморфизма. Когда Isomorphic является false, Map пуст. Наихудшая временная сложность O(N!), где N является число узлов.

[Isomorphic, Map] = graphisomorphism(G1, G2,'Directed', DirectedValue) указывает, направлены ли графики или не направлены. Задайте DirectedValue на false когда оба G1 и G2 являются неориентированными графами. В этом случае верхние треугольники разреженных матриц G1 и G2 игнорируются. По умолчанию это true, что означает, что оба графиков направлены.

Примеры

Создайте и просмотрите ориентированный график с 8 узлами и 11 ребрами.

m('ABCDEFGH') = [1 2 3 4 5 6 7 8];
g1 = sparse(m('ABDCDCGEFFG'),m('BCBDGEEFHGH'),true,8,8)

g1 =

   (1,2)        1
   (4,2)        1
   (2,3)        1
   (3,4)        1
   (3,5)        1
   (7,5)        1
   (5,6)        1
   (4,7)        1
   (6,7)        1
   (6,8)        1
   (7,8)        1

view(biograph(g1,'ABCDEFGH'))

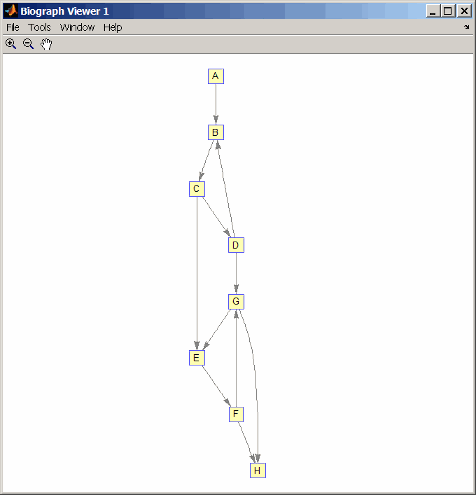
Установите случайный вектор сочетания, а затем создайте и просмотрите новый перестановочный график.
```
p = randperm(8)
 
p =

     7     8     2     3     6     4     1     5

g2 = g1(p,p);
view(biograph(g2,'12345678'))
```
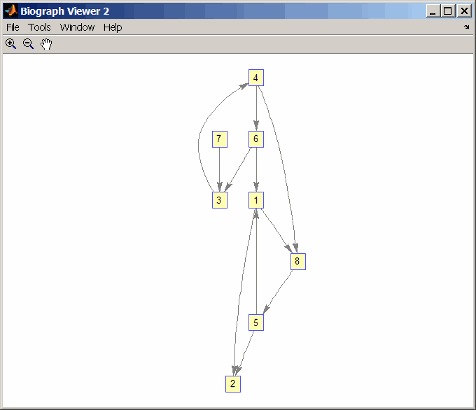
Проверьте, являются ли эти два графиков изоморфными.
```
[F,Map] = graphisomorphism(g2,g1)

F =

     1


Map =

     7     8     2     3     6     4     1     5
```
Обратите внимание, что Map Вектор-строка, содержащий индексы узлов, которые сопоставлены с g2 на g1 является таким же, как вектор сочетания, созданный вами на шаге 2.
Измените направление ребра D-G в первом графике, а затем снова проверьте на изоморфность.
```
g1(m('DG'),m('GD')) = g1(m('GD'),m('DG'));
view(biograph(g1,'ABCDEFGH'))
```
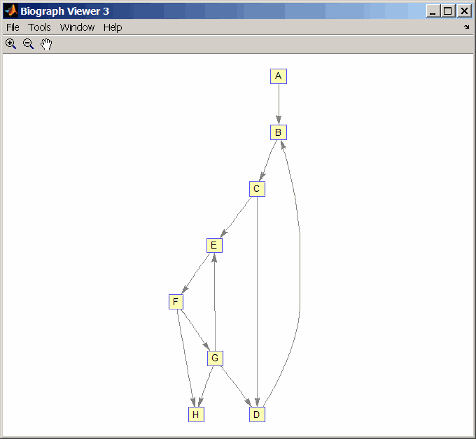
```
[F,M] = graphisomorphism(g2,g1)

F =

     0


M =

     []
```
Преобразуйте графики в неориентированные графы, а затем проверяйте на изоморфность.
```
[F,M] = graphisomorphism(g2+g2',g1+g1','directed',false)

F =

     1


M =

     7     8     2     3     6     4     1     5
```

Ссылки

[1] Фортин, С. (1996). Задача изоморфизма графика. Технический отчет, 96-20, департамент компьютерных наук, Университет Альберты, Эдомонтон, Альберта, Канада.

[2] McKay, B.D. (1981). Практический изоморфизм графика. Конгресс-нумерация 30, 45-87.

[3] Siek, J.G., Lee, L-Q, and Lumsdaine, A. (2002). Руководство пользователя библиотеки График (Upper Saddle River, NJ: Pearson Education).

См. также

Введенный в R2006b

Документация