Первым шагом в многомерном анализе временных рядов является получение, просмотр и предварительная обработка данных. В этом разделе описывается следующее:
Как загрузить экономические данные в MATLAB®
Соответствующие типы данных и структуры для многомерных функций анализа временных рядов
Общие характеристики данных временных рядов, которые могут потребовать преобразования набора перед продолжением анализа
Как разбить ваши данные на предварительные выборки, оценки и прогнозы.
Два основных типа многомерных данных временных рядов:
Данные отклика - Наблюдения из n-D многомерных временных рядов откликов y t (см. Типы стационарных многомерных временных моделей).
Экзогенные данные - Наблюдения из m-D многомерных временных рядов xt предикторов. Каждая переменная в экзогенных данных по умолчанию появляется во всех уравнениях отклика.
Прежде чем задавать любой набор данных как вход в Econometrics Toolbox™ функции, форматируйте данные соответствующим образом. Используйте стандартные команды MATLAB или обработайте данные с помощью программы для электронных таблиц, программы базы данных, PERL или другого инструмента.
Можно получить исторические данные временных рядов из нескольких свободно доступных источников, таких как База экономических данных Федерального резерва Сент-Луиса (известная как FRED®): https://research.stlouisfed.org/fred2/. Если у вас есть лицензия Datafeed Toolbox™, можно использовать функции тулбокса для доступа к данным из различных источников.
Файл Data_USEconModel поставляется с Econometrics Toolbox. Он содержит временные ряды от FRED.
Загрузите данные в Рабочее пространство MATLAB.
load Data_USEconModelПеременные в рабочей области включают:
Data, матрица 249 на 14, содержащая 14 макроэкономических временных рядов.
DataTableмассив расписания MATLAB 249 на 14, содержащий данные с временной меткой.
datesвектор с 249 элементами, содержащий серийные номера дат MATLAB, представляющие даты дискретизации. Серийный номер даты - это количество дней с 1 января 0000 года. (Эта «дата» не является реальной датой, но удобна для проведения вычислений даты. Для получения дополнительной информации см. Форматы дат в Руководстве пользователя Financial Toolbox™.)
DescriptionСимвольный массив, содержащая описание ряда данных и ключ к меткам для каждой серии.
series, массив ячеек меток 1 на 14 для временных рядов.
DataTable содержит те же данные, что и Data. Однако, как и таблица, расписание позволяет вам использовать запись через точку для доступа к переменной. Для примера, DataTable.UNRATE задает временные ряды уровня безработицы. Все расписания содержат переменную Time, который является datetime вектор временных меток наблюдения. Для получения дополнительной информации смотрите Создание Timetables и Представление дат и времени в MATLAB. Можно также работать с серийными номерами дат MATLAB, хранящимися в dates.
Отображение первого и последнего времени дискретизации и имен переменных при помощи DataTable.
firstperiod = DataTable.Time(1)
firstperiod = datetime
Q1-47
lastperiod = DataTable.Time(end)
lastperiod = datetime
Q1-09
seriesnames = DataTable.Properties.VariableNames
seriesnames = 1x14 cell
Columns 1 through 6
{'COE'} {'CPIAUCSL'} {'FEDFUNDS'} {'GCE'} {'GDP'} {'GDPDEF'}
Columns 7 through 12
{'GPDI'} {'GS10'} {'HOANBS'} {'M1SL'} {'M2SL'} {'PCEC'}
Columns 13 through 14
{'TB3MS'} {'UNRATE'}
Эта таблица описывает переменные в DataTable.
| Переменная FRED | Описание |
|---|---|
COE | Выплачена компенсация работникам в миллиарды долларов |
CPIAUCSL
| Индекс потребительских цен (ИПЦ) |
FEDFUNDS | Эффективная ставка федеральных средств |
GCE | Расходы правительства на потребление и инвестиции в миллиарды долларов |
GDP | Валовой внутренний продукт (ВВП) |
GDPDEF | Валовой внутренний продукт в млрд. долл. США |
GPDI | Валовые частные внутренние инвестиции в миллиарды долларов |
GS10 | Десятилетнее выражение казначейских облигаций |
HOANBS | Некоммерческий индекс рабочего времени в бизнес-секторе |
M1SL | M1 денежная масса (узкие деньги) |
M2SL | M2 денежная масса (большие деньги) |
PCEC | Расходы на личное потребление в миллиарды долларов |
TB3MS | Трехмесячный казначейский счет выражения |
UNRATE | Уровень безработицы |
Рассмотрим изучение динамики ВВП, ИПЦ и уровня безработицы, и предположим, что государственные расходы на потребление являются экзогенной переменной. Создайте массивы для данных отклика и предиктора. Отображение последних наблюдений в каждом массиве.
Y = DataTable{:,["CPIAUCSL" "UNRATE" "GDP"]};
x = DataTable.GCE;
lastobsresponse = Y(end,:)lastobsresponse = 1×3
104 ×
0.0213 0.0008 1.4090
lastobspredictor = x(end)
lastobspredictor = 2.8833e+03
Y и x представляют один путь наблюдений и соответствующим образом форматированы для передачи в многомерные функции объекта модели. Информация о временной метке не применяется к массивам, потому что анализы предполагают, что время дискретизации распределено равномерно.
Обычно вы загружаете наборы данных отклика и предиктора в Рабочее пространство MATLAB в виде числовых массивов, таблиц MATLAB или расписаний MATLAB. Однако многомерные функции временных рядов объекта принимают только 2-D или 3-D числовых массивов, и вы должны задать данные отклика и предиктора как отдельные входы.
Тип переменной и контекст задачи определяют формат данных, которые вы поставляете. Для любого массива, содержащего многомерные данные временных рядов:
Строка t массива содержит наблюдения всех переменных в t времени.
Столбец j массива содержит все наблюдения переменных j. MATLAB обрабатывает каждую переменную в массиве как отдельную.
Матрица данных указывает один путь расчета. Чтобы создать переменную, представляющую один путь длины T данных отклика, поместите данные в T -by n матрицу Y:
Y = y j,t, который является t наблюдения переменной отклика j. Один путь данных, созданных из переменных-предикторов или других переменных, имеет сходную форму.(t, j)
Можно задать один путь наблюдений как вход для всех многомерных функций объекта модели, которые принимают данные. Примеры ситуаций, в которых вы поставляете один путь, включают:
Подгонка данных отклика и предиктора к модели VARX. Вы предоставляете как путь данных отклика, так и путь данных предиктора, см. estimate.
Инициализируйте модель VEC с путем предварительной выборки данных для прогнозирования или симуляции путей (см. forecast или simulate).
Получите один путь ответа от фильтрации пути инноваций через модель VAR (см. filter).
Сгенерируйте условные прогнозы из модели VAR, задав путь будущих данных отклика (см. forecast).
3-D числовой массив указывает несколько независимых путей расчета данных. Можно создать T -by- n -by- p массив Y, представляющий p пути расчета данных отклика, путем сложения единичных путей откликов (матриц) вдоль третьей размерности.

Y = y j, t, k, что является t наблюдения переменной отклика j от пути k, k = 1,..., p. Все пути должны иметь одинаковые шаги расчета, и переменные среди путей должны соответствовать. Для получения дополнительной информации см. Раздел «Многомерные массивы»(t, j, k)
Можно задать массив из нескольких путей откликов или инноваций в качестве входов для нескольких многомерных функций объекта модели, которые принимают данные. Примеры ситуаций, в которых вы поставляете несколько путей, включают:
Инициализируйте модель VEC с несколькими путями предварительных образцов данных для прогнозирования или симуляции нескольких путей. Каждый заданный путь может представлять различные начальные условия, из которых функции генерируют прогнозы или симуляции.
Получите несколько путей отклика от фильтрации нескольких путей инноваций через модель VAR. Этот процесс является альтернативным способом моделирования нескольких путей отклика.
Сгенерируйте несколько условных путей прогноза из модели VAR, учитывая несколько путей будущих данных отклика.
estimate не поддерживает спецификацию нескольких путей ответных данных.
Все многомерные функции объекта модели, которые берут экзогенные данные как вход, принимают матрицу X, представляющую один путь наблюдений. MATLAB включает все экзогенные переменные в регрессионый компонент каждого уравнения отклика. Для модели VAR (p) уравнения отклика:
Чтобы сконфигурировать регрессионные компоненты уравнений отклика, работайте с матрицей коэффициента регрессии (сохраненной в Beta свойство объекта модели), а не данные. Для получения дополнительной информации см. «Создание модели VAR» и «Выбор экзогенных переменных для уравнений отклика».
Многомерные функции объекта модели не поддерживают несколько путей данных предиктора. Однако, если вы задаете путь данных предиктора и нескольких путей отклика или данных инноваций, функция связывает одни и те же данные предиктора со всеми путями. Для примера, если вы моделируете пути ответов из модели VARX и задаете несколько путей значений предварительного образца, simulate применяет те же экзогенные данные к каждому сгенерированному пути отклика.
Ваши данные могут иметь характеристики, которые нарушают допущения модели. Например, у вас могут быть данные с экспоненциальным ростом или данные из нескольких источников с различными периодичностями. В таких случаях предварительно обработайте или преобразуйте данные в приемлемую форму для анализа.
Осмотрите данные по отсутствующим значениям, которые обозначены NaNs. По умолчанию функции объекта используют списковое удаление, чтобы удалить наблюдения, содержащие по крайней мере одно отсутствующее значение. Если хотя бы один ответ или переменная предиктора имеет отсутствующее значение для временной точки (строки), MATLAB удаляет все наблюдения за это время (вся строка матриц отклика и данных предиктора). Такое удаление может иметь последствия для временной основы и эффективного размера выборки. Поэтому перед началом анализа необходимо изучить и устранить любые отсутствующие значения.
Для данных из нескольких источников необходимо решить, как синхронизировать данные. Синхронизация данных может включать агрегирование или дезагрегацию данных, а последняя может создавать шаблоны отсутствующих значений. Вы можете обратиться к этим типам индуцированных отсутствующих значений путем ввода предыдущих значений (то есть отсутствующее значение не изменяется по сравнению с его предыдущим значением) или путем интерполяции их из соседних значений.
Если временные ряды являются переменными в расписании, то можно синхронизировать данные при помощи synchronize.
Для временных рядов, демонстрирующих экспоненциальный рост, можно предварительно обработать данные, взяв логарифм растущего ряда. В некоторых случаях необходимо применить первое различие результата (см. price2ret). Для получения дополнительной информации о стабилизации временных рядов, смотрите Unit Root Nonstationarity. Например, см. Пример модели VAR.
Примечание
Если применить первое различие ряда, полученный ряд на одно наблюдение короче, чем исходный ряд. Если вы применяете первое различие только некоторых временных рядов в наборе данных, обрезайте другой ряд так, чтобы все имели одинаковую длину, или дополните дифференцированный ряд начальными значениями.
Когда вы подбираете модель временных рядов к данным, отстающие члены в модели требуют инициализации, обычно с наблюдениями в начале выборки. Кроме того, чтобы измерить качество прогнозов из модели, вы должны удержать данные в конце выборки из оценки. Поэтому перед анализом данных разбейте временную основу на трёх последовательных несвязанных интервалов:
Три временные основы для многомерных моделей вектора авторегрессии (VAR) и вектора коррекции ошибок (VEC) являются предварительной выборкой, оценочным и прогнозным периодами.
Период предварительной выборки - содержит данные, используемые для инициализации отстающих значений в модели. И модели VAR (p), и модели VEC (p-1) требуют периода предварительного образца, содержащего по крайней мере p многомерных наблюдений. Например, если Вы планируете соответствовать модели VAR (4), условное ожидаемое значение <reservedrangesplaceholder19> <reservedrangesplaceholder18>, учитывая его историю, содержит <reservedrangesplaceholder17> <reservedrangesplaceholder16> - 1, <reservedrangesplaceholder15> <reservedrangesplaceholder14> - 2, <reservedrangesplaceholder13> <reservedrangesplaceholder12> - 3, и <reservedrangesplaceholder11> <reservedrangesplaceholder10> - 4. Условное ожидаемое значение y 5 является функцией y 1, y 2, y 3 и y 4. Поэтому вклад вероятности y 5 требует y 1- y 4, что подразумевает, что данных для вклада вероятности y 1- y 4 не существует. В этом случае оценка модели требует периода предварительного образца, по меньшей мере, четырех временных точек.
Период оценки - содержит наблюдения, к которым модель явно подходит. Количество наблюдений в выборке оценки effective sample size. Для идентифицируемости параметра эффективным размером выборки должно быть, по крайней мере, количество оцениваемых параметров.
Период прогноза - дополнительный период, в течение которого генерируются прогнозы, известный как forecast horizon. Этот раздел содержит данные holdout для валидации предсказуемости модели.
Предположим y t является рядом 2-D отклика и x t является 1-D экзогенным рядом. Считайте подбор кривой VARX (<reservedrangesplaceholder4>) моделью <reservedrangesplaceholder3> <reservedrangesplaceholder2> к данным ответа в матрице <reservedrangesplaceholder1>-by-2 Y и экзогенные данные в векторе T -by-1 x. Кроме того, вы хотите, чтобы прогнозируемый горизонт имел K длины (то есть вы хотите продержаться K наблюдениях в конце выборки, чтобы сравнить с прогнозами из подобранной модели). Этот рисунок показывает разбиения основы времени для оценки модели.
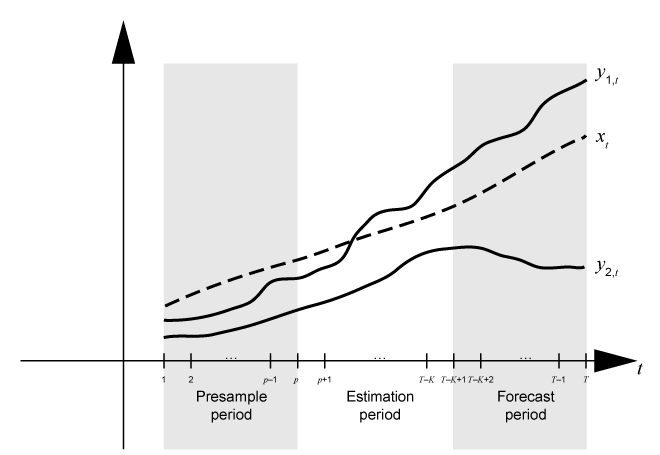
Этот рисунок показывает фрагменты из массивов, которые соответствуют входным параметрам из estimate функция.
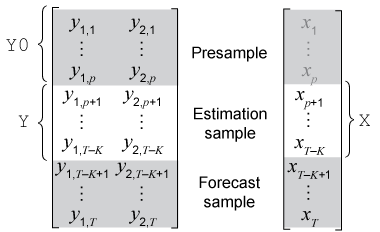
Y - необходимый вход для определения данных отклика, к которым подходит модель.
Y0 является необязательным аргументом пары "имя-значение" для определения предварительных данных отклика. Y0 должно иметь не менее p строк. Чтобы инициализировать модель, estimate использует только последние наблюдения p Y0 ((end - .p + 1): конец,:)
X является необязательным аргументом пары "имя-значение" для определения экзогенных данных для линейного регрессионого компонента. По умолчанию, estimate исключает из модели регрессионный компонент независимо от значения коэффициента регрессии Beta от arima шаблон модели для оценки.
Если вы не задаете 'Y0', estimate удаляет наблюдения с 1 по p из Y чтобы инициализировать модель, а затем подгоняет модель к остальным данным Y (. То есть, (p + 1): конец,:)estimate выводит периоды предварительной выборки и оценки из Y. Хотя estimate извлекает предварительную выборку из Y по умолчанию можно извлечь предварительную выборку из данных и указать его с помощью Y0 аргумент пары "имя-значение", который гарантирует, что estimate инициализирует и подбирает модель к вашим спецификациям.
Если вы задаете 'X':
estimate синхронизирует X и Y относительно последнего наблюдения в массивах (T - K на предыдущем рисунке) и применяет только необходимое количество наблюдений к регрессионному компоненту. Это действие подразумевает, что X может иметь больше строк, которые Y.
Если вы также задаете 'Y0', estimate использует только последние экзогенные наблюдения, необходимые для подгонки модели (наблюдения J + 1 до T - K на предыдущем рисунке). estimate игнорирует предварительные экзогенные данные.
Если вы планируете подтвердить прогнозирующую степень подобранной модели, необходимо извлечь прогнозную выборку из набора данных перед оценкой.
Рассмотрите подбор кривой модели VAR (4) к данным и переменным в Load Multivariate Economic Data и сохранение последних 2 лет данных, чтобы подтвердить прогнозирующую степень подобранной модели .
Загрузите данные. Создайте расписание, содержащее переменные предиктора и отклика
load Data_USEconModel responsenames = ["CPIAUCSL" "UNRATE" "GDP"]; predictorname = "GCE"; TT = DataTable(:,[responsenames predictorname]);
Идентифицируйте все строки в расписании, содержащем по крайней мере одно отсутствующее наблюдение (NaN).
whichmissing = ismissing(TT); idxvar = sum(whichmissing) > 0; hasmissing = TT.Properties.VariableNames(idxvar)
hasmissing = 1x1 cell array
{'UNRATE'}
wheremissing = find(whichmissing(:,idxvar) > 0)
wheremissing = 4×1
1
2
3
4
Уровень безработицы пропускает первый год данных в выборке.
Удалите наблюдения (строки) с начальными отсутствующими значениями из данных.
TT = rmmissing(TT);
rmmissing использует listwise deletion, чтобы удалить все строки из входного расписания, содержащего по крайней мере одно отсутствующее наблюдение.
Модель VAR (4) требует 4 предварительных ответов, а прогнозная выборка требует 2 лет (8 четвертей) данных. Разделите данные отклика на предварительно выбранные, оценочные и прогнозные переменные выборки. Разделите данные предиктора на переменные выборки оценки и прогноза (предварительный образец данных предиктора не рассматривается как оценка).
p = 4; % Num. presample observations fh = 8; % Forecast horizon T = size(TT,1); % Total sample size eT = T - p - fh; % Effective sample size idxpre = 1:p; idxest = (p + 1):(T - fh); idxfor = (T - fh + 1):T; Y0 = TT{idxpre,responsenames}; % Presample responses YF = TT{idxfor,responsenames}; % Forecast sample responses Y = TT{idxest,responsenames}; % Estimation sample responses xf = TT{idxfor,predictorname}; x = TT{idxest,predictorname};
При оценке модели используйте estimate, задайте varm шаблон модели, представляющий модель VAR (4) и данные отклика выборки оценки Y в качестве входов. Задайте предварительные данные отклика Y0 для инициализации модели с помощью 'Y0' аргумент пары "имя-значение" и задайте данные предиктора выборки оценки x при помощи 'X' аргумент пары "имя-значение". Y и x синхронизируются наборы данных, в то время как Y0 происходит в течение предыдущих четырех периодов, прежде чем начинается выборка оценки.
После оценки можно спрогнозировать модель с помощью forecast путем определения предполагаемого объекта модели VARX (4), возвращенного estimate, горизонт прогноза fh, и оценка выборочных данных отклика Y чтобы инициализировать модель для прогнозирования. Задайте прогнозные выборочные данные предиктора xf для компонента регрессии модели при помощи 'X' аргумент пары "имя-значение". Определите прогнозирующую степень модели оценки путем сравнения прогнозов с данными отклика выборки прогноза YF.