Чтобы создать полностью заданную задачу оптимизации портфеля средних дисперсий, создайте экземпляр Portfolio объект, использующий Portfolio. Для получения информации о рабочем процессе при использовании Portfolio объекты, см. раздел Рабочий процесс объекта портфеля.
Использование Portfolio чтобы создать образец объекта Portfolio класс. Можно использовать Portfolio несколькими способами. Чтобы настроить задачу оптимизации портфеля в Portfolio объект, самый простой синтаксис:
p = Portfolio;
Portfolio объект, p, таким образом, что все свойства объекта пусты. The Portfolio объект также принимает наборы аргументов пары "имя-значение" аргументов для свойств и их значений. The Portfolio объект принимает входы для общественной собственности с общим синтаксисом:
p = Portfolio('property1', value1, 'property2', value2, ... );Если a Portfolio объект уже существует, синтаксис разрешает первый (и только первый аргумент) из Portfolio быть существующим объектом с последующими аргументами пары "имя-значение" для свойств, которые будут добавлены или изменены. Для примера, учитывая существующее Portfolio объект в pОбщий синтаксис:
p = Portfolio(p, 'property1', value1, 'property2', value2, ... );
Входные параметры не зависят от регистра, но должны быть полностью заданы. Кроме сложения, несколько свойств могут быть заданы с помощью альтернативных имен аргумента (см. Ярлыки для Имен свойства). The Portfolio объект обнаруживает размерности задачи из входов и, после того, как набор, последующие входы могут подвергаться различным скалярным или матричным операциям расширения, которые упрощают общий процесс для формирования задачи. В сложение a Portfolio объект является объектом значения, так что, данный портфель pследующий код создает два объекта, p и q, которые являются различными:
q = Portfolio(p, ...)
Оптимизация портфеля средних дисперсий полностью задана с помощью Portfolio объект, если эти два условия удовлетворены:
Моменты возвратов активов должны быть заданы таким образом, чтобы свойство AssetMean содержит действительный конечный вектор средних значений возвратов активов и свойства AssetCovar содержит действительную симметричную положительно-полуопределенную матрицу для ковариации возвратов активов.
Первое условие удовлетворяется установкой свойств, связанных с моментами возвратов активов.
Набор допустимых портфелей должен быть непустым компактным набором, где компактный набор закрыт и ограничен.
Второе условие удовлетворяет обширному набору свойств, которые определяют различные типы ограничений, чтобы сформировать набор допустимых портфелей. Поскольку такие наборы должны быть ограничены, могут быть наложены явные или неявные ограничения, и несколько функций, таких как estimateBounds, предоставить способы, чтобы убедиться, что ваша проблема правильно сформулирована.
Хотя общие условия достаточности для оптимизации портфеля средних дисперсий выходят за эти два условия, Portfolio объект, реализованный в Financial Toolbox™, неявно обрабатывает все эти дополнительные условия. Для получения дополнительной информации о модели Марковица для оптимизации портфеля со средними дисперсиями, смотрите Оптимизация портфеля.
Если вы создаете Portfolio объект, pбез входных параметров можно отобразить его с помощью disp:
p = Portfolio; disp(p)
Portfolio with properties:
BuyCost: []
SellCost: []
RiskFreeRate: []
AssetMean: []
AssetCovar: []
TrackingError: []
TrackingPort: []
Turnover: []
BuyTurnover: []
SellTurnover: []
Name: []
NumAssets: []
AssetList: []
InitPort: []
AInequality: []
bInequality: []
AEquality: []
bEquality: []
LowerBound: []
UpperBound: []
LowerBudget: []
UpperBudget: []
GroupMatrix: []
LowerGroup: []
UpperGroup: []
GroupA: []
GroupB: []
LowerRatio: []
UpperRatio: []
MinNumAssets: []
MaxNumAssets: []
BoundType: [] Перечисленные подходы обеспечивают способ настроить задачу оптимизации портфеля с Portfolio объект. The set функции предлагают дополнительные способы задать и изменить наборы свойств в Portfolio объект.
Можно использовать Portfolio объект, чтобы непосредственно настроить «стандартную» задачу оптимизации портфеля, учитывая среднее значение и ковариацию возвратов активов в переменных m и C:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio('assetmean', m, 'assetcovar', C, ...
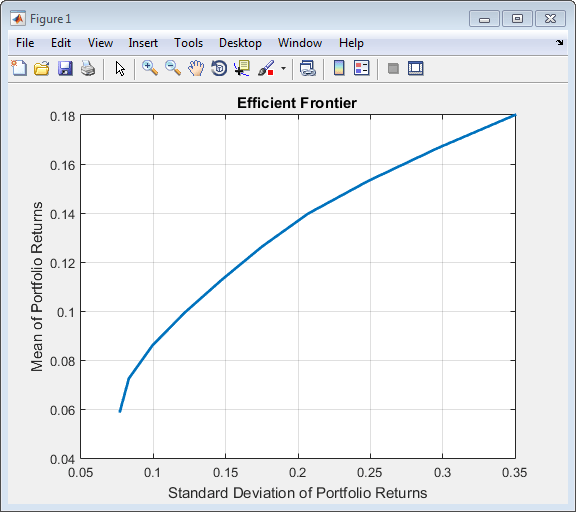
'lowerbudget', 1, 'upperbudget', 1, 'lowerbound', 0);LowerBound значение свойства подвергается скалярному расширению, так как AssetMean и AssetCovar обеспечивают размерности задачи.Вы можете использовать запись через точку с функцией plotFrontier.
p.plotFrontier
Альтернативный способ выполнить ту же задачу настройки «стандартной» задачи оптимизации портфеля, учитывая среднее значение и ковариацию возвратов активов в переменных m и C (что также иллюстрирует, что имена аргумента не зависят от регистра):
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p = Portfolio(p, 'assetmean', m, 'assetcovar', C);
p = Portfolio(p, 'lowerbudget', 1, 'upperbudget', 1);
p = Portfolio(p, 'lowerbound', 0);
plotFrontier(p)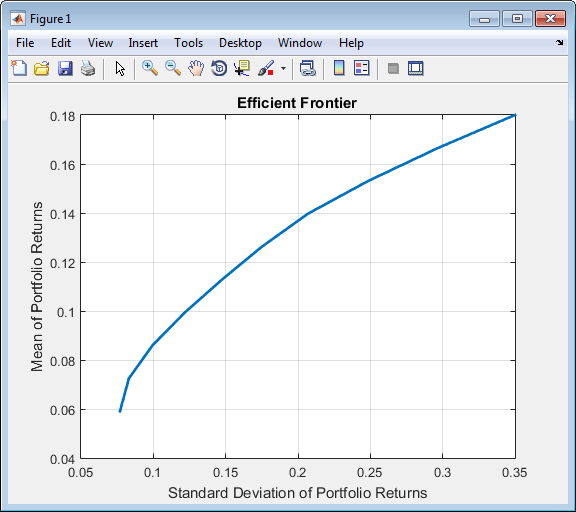
Этот способ работает, потому что вызовы в Portfolio находятся в этом конкретном порядке. В этом случае вызов для инициализации AssetMean и AssetCovar предоставляет размерности для задачи. Если бы вы сделали этот шаг последним, вам пришлось бы явно измерить LowerBound свойство следующим образом:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p = Portfolio(p, 'LowerBound', zeros(size(m)));
p = Portfolio(p, 'LowerBudget', 1, 'UpperBudget', 1);
p = Portfolio(p, 'AssetMean', m, 'AssetCovar', C);
plotFrontier(p)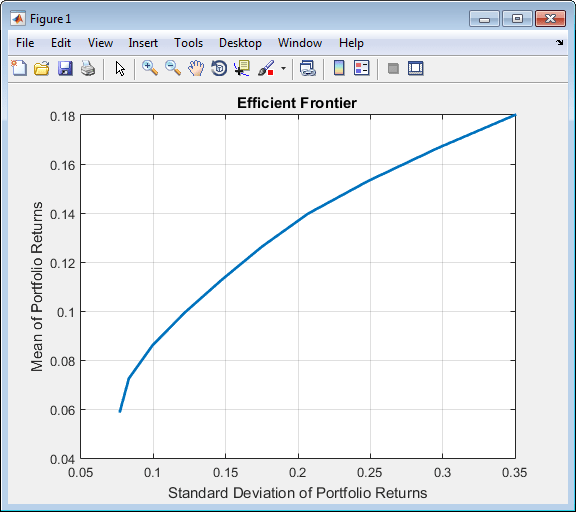
Если вы не указали размер LowerBound но вместо этого введите скалярный аргумент, Portfolio объект принимает, что вы определяете проблему с одним активом и вызывает ошибку при вызове установки моментов с четырьмя активами.
The Portfolio объект имеет более короткие имена аргумента, которые заменяют более длинные имена аргумента, сопоставленные с конкретными свойствами Portfolio объект. Для примера, а не вводите 'assetcovar', а Portfolio объект принимает имя без учета регистра 'covar' для установки AssetCovar свойство в Portfolio объект. Каждое более короткое имя аргумента соответствует одному свойству в Portfolio объект. Единственным исключением является имя альтернативного аргумента 'budget', что означает оба LowerBudget и UpperBudget свойства. Когда 'budget' используется, затем LowerBudget и UpperBudget свойства заданы в том же значении, чтобы сформировать ограничение бюджета равенства.
Ярлыки для имен свойства
Имя аргумента ярлыка | Эквивалентный аргумент/имя свойства |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для примера этот вызов Portfolio использует эти ярлыки для свойств и эквивалентно предыдущим примерам:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio('mean', m, 'covar', C, 'budget', 1, 'lb', 0);
plotFrontier(p)
Несмотря на то, что не рекомендуемый, вы можете задать свойства непосредственно, однако на ваших входах не выполняется проверка ошибок:
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p.NumAssets = numel(m);
p.AssetMean = m;
p.AssetCovar = C;
p.LowerBudget = 1;
p.UpperBudget = 1;
p.LowerBound = zeros(size(m));
plotFrontier(p)