portoptЭтот пример изображает эффективную границу гипотетического портфеля из трех активов. Он иллюстрирует, как задать ожидаемые возвраты, стандартные отклонения и корреляции портфеля активов, как преобразовать стандартные отклонения и корреляции в ковариационную матрицу и как вычислить и построить эффективный рубеж из возвратов и ковариаций. Пример также иллюстрирует, как случайным образом сгенерировать набор весов портфеля и как добавить случайные портфели к существующему графику для сравнения с эффективной границей.
Во-первых, задайте ожидаемые возвраты, стандартные отклонения и матрицу корреляции для гипотетического портфеля из трех активов.
Returns = [0.1 0.15 0.12];
STDs = [0.2 0.25 0.18];
Correlations = [ 1 0.3 0.4
0.3 1 0.3
0.4 0.3 1 ];
Преобразуйте стандартные отклонения и корреляционную матрицу в дисперсионно-ковариационную матрицу с функцией corr2cov.
Covariances = corr2cov(STDs, Correlations);
Оцените и постройте график эффективной границы в 20 точках вдоль границы, используя функцию portopt и ожидаемые возвраты и соответствующая ковариационная матрица. Хотя на активы в портфеле могут быть наложены довольно сложные ограничения, для простоты примите ограничения по умолчанию и масштабируйте общее значение портфеля до 1 и ограничьте веса положительными (без коротких продаж).
Примечание
portopt был частично удален и больше не будет принимать ConSet или varargin аргументы. Использование Portfolio вместо этого объект для решения портфельных задач, которые больше, чем долгосрочный, полностью вложенный портфель. Дополнительные сведения о рабочем процессе при использовании объектов Portfolio см. в разделе Рабочий процесс объекта портфеля. Для получения дополнительной информации о миграции portopt код для Portfolio, см. Перенос портфеля на объект портфеля.
portopt(Returns, Covariances, 20)
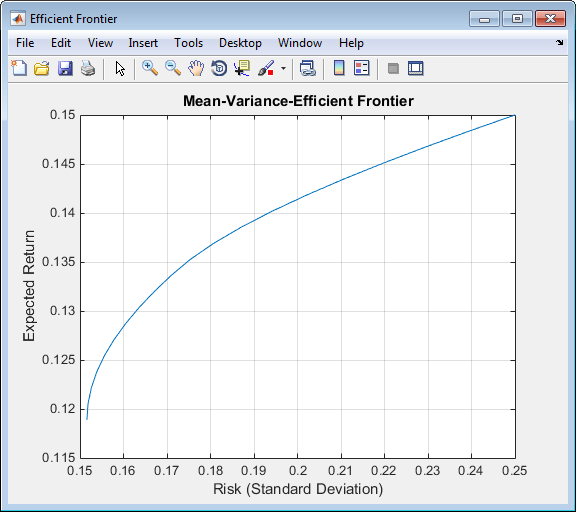
Теперь, когда отображается эффективная граница, случайным образом сгенерируйте веса основных средств для 1000 портфелей, начиная с MATLAB® начальное состояние.
rng('default')
Weights = rand(1000, 3);Предыдущая строка кода генерирует три столбца равномерно распределенных случайных весов, но не гарантирует, что они равны 1. Следующий сегмент кода нормализует веса каждого портфеля так, чтобы общая сумма трех весов представляла собой действительный портфель.
Total = sum(Weights, 2); % Add the weights Total = Total(:,ones(3,1)); % Make size-compatible matrix Weights = Weights./Total; % Normalize so sum = 1
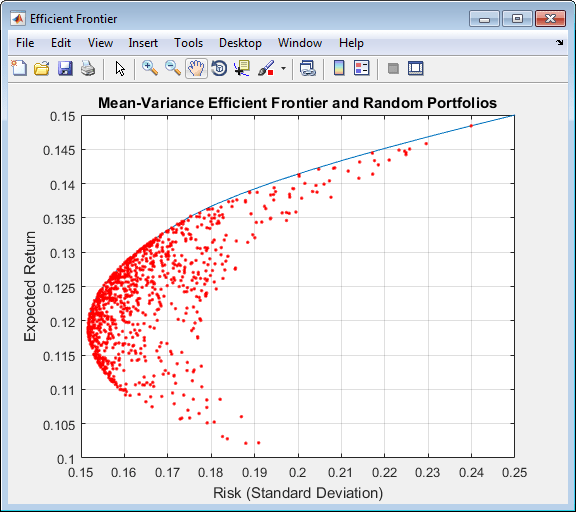
Учитывая созданные 1000 случайных портфелей, вычислите ожидаемый возврат и риск каждого портфеля, связанный с весами.
[PortRisk, PortReturn] = portstats(Returns, Covariances, ...
Weights);
Наконец, сохраните текущий график и постройте график возвратов и рисков каждого портфеля поверх существующей эффективной границы для сравнения. После графического изображения аннотируйте график заголовком и верните график к статусу удержания по умолчанию (любые последующие графики будут удалять существующие данные). Эффективная граница появляется синим цветом, в то время как 1000 случайных портфелей появляются как набор красных точек на или ниже границы.
hold on plot (PortRisk, PortReturn, '.r') title('Mean-Variance Efficient Frontier and Random Portfolios') hold off
blsdelta | blsgamma | blsprice | blsvega | bndconvy | bnddury | bndkrdur | bndprice | corr2cov | portopt | zbtprice | zero2disc | zero2fwd