Exponenta Banner

bdtprice

Цены на инструменты из дерева процентных ставок Black-Derman-Toy

Свернуть все на странице

Синтаксис

[Price,PriceTree] = bdtprice(BDTTree,InstSet)
[Price,PriceTree] = bdtprice(___,Options)

Описание

пример

[Price,PriceTree] = bdtprice(BDTTree,InstSet) вычисляет бесплатные арбитражные цены на инструменты с помощью дерева процентных ставок, созданного с bdttree. Все инструменты, содержащиеся в переменной финансового инструмента, InstSet, оценены.

bdtprice обрабатывает типы инструментов: 'Bond', 'CashFlow', 'OptBond', 'OptEmBond', 'OptFloat', 'OptEmFloat', 'Fixed', 'Float', 'Cap', 'Floor', 'RangeFloat', 'Swap'. Посмотрите instadd для создания определенных типов.

пример

[Price,PriceTree] = bdtprice(___,Options) добавляет необязательный входной параметр для Options.

Примеры

свернуть все

Загрузите дерево BDT и инструменты из файла данных deriv.mat для ценообразования прописной буквы и облигационных инструментов, содержащихся в наборе приборов. 

load deriv.mat; 
BDTSubSet = instselect(BDTInstSet,'Type', {'Bond', 'Cap'});

instdisp(BDTSubSet)
instdisp(BDTSubSet)
Index Type CouponRate Settle         Maturity       Period Basis EndMonthRule IssueDate FirstCouponDate LastCouponDate StartDate Face Name     Quantity
1     Bond 0.1        01-Jan-2000    01-Jan-2003    1      NaN   NaN          NaN       NaN             NaN            NaN       NaN  10% Bond 100     
2     Bond 0.1        01-Jan-2000    01-Jan-2004    2      NaN   NaN          NaN       NaN             NaN            NaN       NaN  10% Bond  50     
 
Index Type Strike Settle         Maturity       CapReset Basis Principal Name    Quantity
3     Cap  0.15   01-Jan-2000    01-Jan-2004    1        NaN   NaN       15% Cap 30

Оцените облигацию и прописную букву.

[Price, PriceTree] = bdtprice(BDTTree, BDTSubSet)
Warning: Not all cash flows are aligned with the tree. Result will be approximated. 
> In checktree at 289
  In bdtprice at 85 

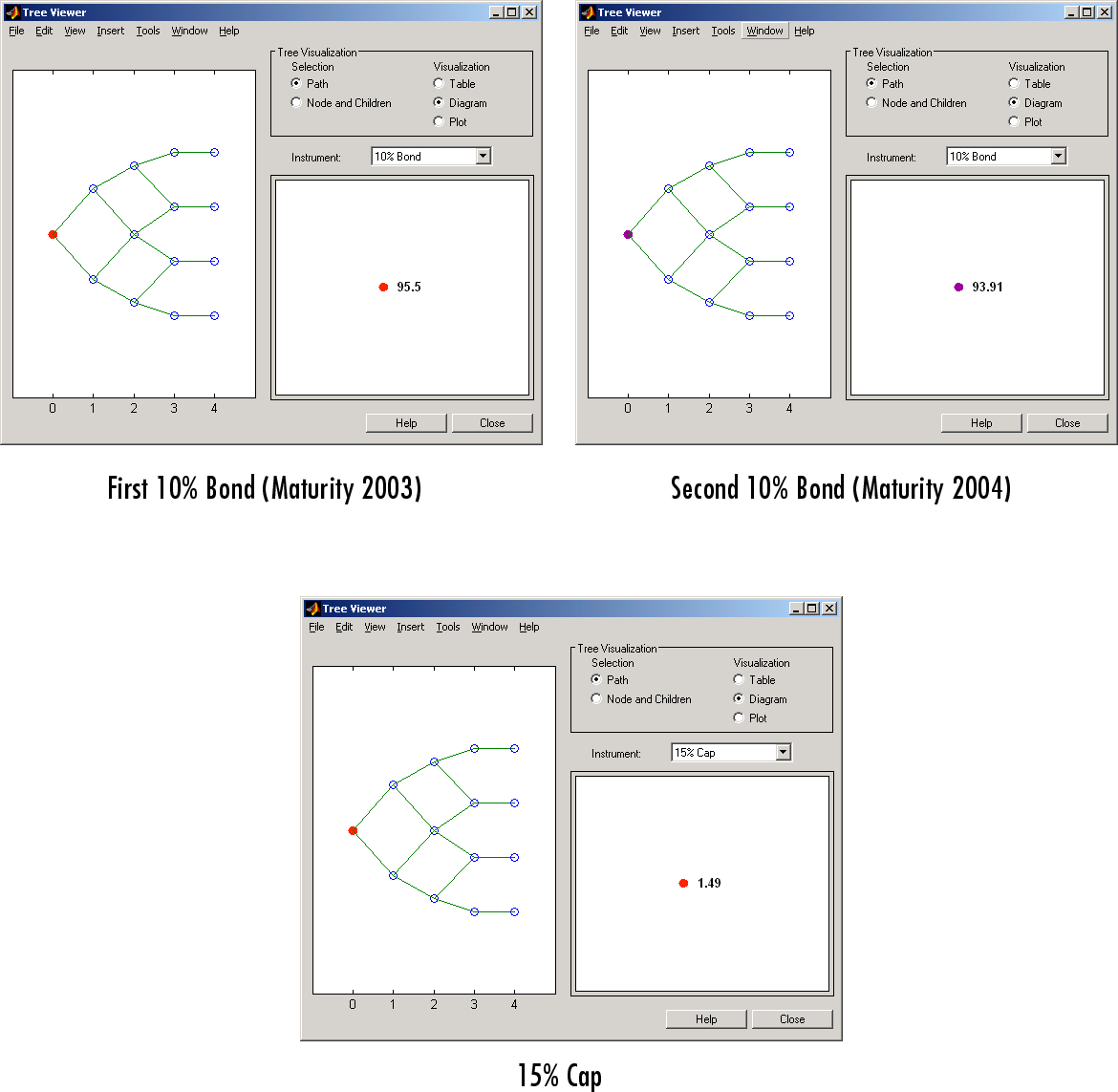
Price =

   95.5030
   93.9079
    1.4375


PriceTree = 

    FinObj: 'BDTPriceTree'
     PTree: {[3x1 double]  [3x2 double]  [3x3 double]  [3x4 double]  [3x4 double]}
    AITree: {[3x1 double]  [3x2 double]  [3x3 double]  [3x4 double]  [3x4 double]}
      tObs: [0 1 2 3 4]

Вы можете использовать treeviewer функция, чтобы увидеть цены этих трех инструментов вдоль дерева цен.

Открыть Live Script

Оценить следующие многоступенчатые купонные облигации используя следующие данные: 

Rates = [0.035; 0.042147; 0.047345; 0.052707];
ValuationDate = 'Jan-1-2010';
StartDates = ValuationDate;
EndDates = {'Jan-1-2011'; 'Jan-1-2012'; 'Jan-1-2013'; 'Jan-1-2014'};
Compounding = 1;

% Create RateSpec
RS = intenvset('ValuationDate', ValuationDate, 'StartDates', StartDates,...
'EndDates', EndDates,'Rates', Rates, 'Compounding', Compounding);

% Create a portfolio of stepped coupon bonds with different maturities
Settle = '01-Jan-2010';
Maturity = {'01-Jan-2011';'01-Jan-2012';'01-Jan-2013';'01-Jan-2014'};
CouponRate = {{'01-Jan-2011' .042;'01-Jan-2012' .05; '01-Jan-2013' .06; '01-Jan-2014' .07}};

% Display the instrument portfolio 
ISet = instbond(CouponRate, Settle, Maturity, 1);
instdisp(ISet)
Index Type CouponRate Settle         Maturity       Period Basis EndMonthRule IssueDate FirstCouponDate LastCouponDate StartDate Face
1     Bond [Cell]     01-Jan-2010    01-Jan-2011    1      0     1            NaN       NaN             NaN            NaN       100 
2     Bond [Cell]     01-Jan-2010    01-Jan-2012    1      0     1            NaN       NaN             NaN            NaN       100 
3     Bond [Cell]     01-Jan-2010    01-Jan-2013    1      0     1            NaN       NaN             NaN            NaN       100 
4     Bond [Cell]     01-Jan-2010    01-Jan-2014    1      0     1            NaN       NaN             NaN            NaN       100

Создайте BDTTree для оценки ступенчатых купонных облигаций. Предположим, что волатильность составляет 10%

Sigma = 0.1; 
BDTTimeSpec = bdttimespec(ValuationDate, EndDates, Compounding);
BDTVolSpec = bdtvolspec(ValuationDate, EndDates, Sigma*ones(1, length(EndDates))');
BDTT = bdttree(BDTVolSpec, RS, BDTTimeSpec);

% Compute the price of the stepped coupon bonds
PBDT = bdtprice(BDTT, ISet)
PBDT = 4×1

  100.6763
  100.7368
  100.9266
  101.0115
Открыть Live Script

Ценят портфель ступенчатых вызываемых облигаций и ступенчатых ванильных облигаций, используя следующие данные: Данные для структуры процентной ставки:

Rates = [0.035; 0.042147; 0.047345; 0.052707];
ValuationDate = 'Jan-1-2010';
StartDates = ValuationDate;
EndDates = {'Jan-1-2011'; 'Jan-1-2012'; 'Jan-1-2013'; 'Jan-1-2014'};
Compounding = 1;

%Create RateSpec
RS = intenvset('ValuationDate', ValuationDate, 'StartDates', StartDates,...
'EndDates', EndDates,'Rates', Rates, 'Compounding', Compounding);

% Create an instrument portfolio of 3 stepped callable bonds and three
% stepped vanilla bonds
Settle = '01-Jan-2010';
Maturity = {'01-Jan-2012';'01-Jan-2013';'01-Jan-2014'};
CouponRate = {{'01-Jan-2011' .042;'01-Jan-2012' .05; '01-Jan-2013' .06; '01-Jan-2014' .07}};
OptSpec='call';
Strike=100;
ExerciseDates='01-Jan-2011'; %Callable in one year

% Bonds with embedded option 
ISet = instoptembnd(CouponRate, Settle, Maturity, OptSpec, Strike,...
ExerciseDates, 'Period', 1);
                    
% Vanilla bonds 
ISet = instbond(ISet, CouponRate, Settle, Maturity, 1);

% Display the instrument portfolio
instdisp(ISet)
Index Type      CouponRate Settle         Maturity       OptSpec Strike ExerciseDates  Period Basis EndMonthRule IssueDate FirstCouponDate LastCouponDate StartDate Face AmericanOpt
1     OptEmBond [Cell]     01-Jan-2010    01-Jan-2012    call    100    01-Jan-2011    1      0     1            NaN       NaN             NaN            NaN       100  0          
2     OptEmBond [Cell]     01-Jan-2010    01-Jan-2013    call    100    01-Jan-2011    1      0     1            NaN       NaN             NaN            NaN       100  0          
3     OptEmBond [Cell]     01-Jan-2010    01-Jan-2014    call    100    01-Jan-2011    1      0     1            NaN       NaN             NaN            NaN       100  0          
 
Index Type CouponRate Settle         Maturity       Period Basis EndMonthRule IssueDate FirstCouponDate LastCouponDate StartDate Face
4     Bond [Cell]     01-Jan-2010    01-Jan-2012    1      0     1            NaN       NaN             NaN            NaN       100 
5     Bond [Cell]     01-Jan-2010    01-Jan-2013    1      0     1            NaN       NaN             NaN            NaN       100 
6     Bond [Cell]     01-Jan-2010    01-Jan-2014    1      0     1            NaN       NaN             NaN            NaN       100

Создайте BDTTree и цена инструментов. Построение дерева Предположим, что волатильность составляет 10%

Sigma = 0.1;  
BDTTimeSpec = bdttimespec(ValuationDate, EndDates, Compounding);
BDTVolSpec = bdtvolspec(ValuationDate, EndDates, Sigma*ones(1, length(EndDates))');
BDTT = bdttree(BDTVolSpec, RS, BDTTimeSpec);

%The first three rows corresponds to the price of the stepped callable bonds and the
%last three rows corresponds to the price of the stepped vanilla bonds.
PBDT = bdtprice(BDTT, ISet)
PBDT = 6×1

  100.4799
  100.3228
  100.0840
  100.7368
  100.9266
  101.0115
Открыть Live Script

Вычислите цену портфеля с нот области значений и запиской с плавающей ставкой с помощью следующих данных: Данные для структуры терминов процентной ставки следующие:

Rates = [0.035; 0.042147; 0.047345; 0.052707];
ValuationDate = 'Jan-1-2011';
StartDates = ValuationDate;
EndDates = {'Jan-1-2012'; 'Jan-1-2013'; 'Jan-1-2014'; 'Jan-1-2015'};
Compounding = 1;

%  Create RateSpec
RS = intenvset('ValuationDate', ValuationDate, 'StartDates', StartDates,...
'EndDates', EndDates,'Rates', Rates, 'Compounding', Compounding);
  
% Create an instrument portfolio with two range notes and a floating rate
% note with the following data:
Spread = 200;
Settle = 'Jan-1-2011';
Maturity = 'Jan-1-2014';

% First Range Note:
RateSched(1).Dates = {'Jan-1-2012'; 'Jan-1-2013'  ; 'Jan-1-2014'};
RateSched(1).Rates  = [0.045 0.055; 0.0525  0.0675; 0.06 0.08];

% Second Range Note:
RateSched(2).Dates = {'Jan-1-2012'; 'Jan-1-2013' ; 'Jan-1-2014'};
RateSched(2).Rates  = [0.048 0.059; 0.055  0.068 ; 0.07 0.09];

% Create InstSet
InstSet = instadd('RangeFloat', Spread, Settle, Maturity, RateSched);

% Add a floating-rate note
InstSet = instadd(InstSet, 'Float', Spread, Settle, Maturity);

% Display the portfolio instrument
instdisp(InstSet)
Index Type       Spread Settle         Maturity       RateSched FloatReset Basis Principal EndMonthRule
1     RangeFloat 200    01-Jan-2011    01-Jan-2014    [Struct]  1          0     100       1           
2     RangeFloat 200    01-Jan-2011    01-Jan-2014    [Struct]  1          0     100       1           
 
Index Type  Spread Settle         Maturity       FloatReset Basis Principal EndMonthRule CapRate FloorRate
3     Float 200    01-Jan-2011    01-Jan-2014    1          0     100       1            Inf     -Inf

Создайте BDTTree и цена инструментов. Создайте дерево Предположим, что волатильность составляет 10%.

Sigma = 0.1;  
BDTTS = bdttimespec(ValuationDate, EndDates, Compounding);
BDTVS = bdtvolspec(ValuationDate, EndDates, Sigma*ones(1, length(EndDates))');
BDTT = bdttree(BDTVS, RS, BDTTS);

% Price the portfolio 
Price = bdtprice(BDTT, InstSet)
Price = 3×1

  100.2841
   98.0757
  105.5147
Открыть Live Script

Использование instswap чтобы создать своп с плавающей запятой и оценить своп с bdtprice. 

RateSpec = intenvset('Rates',.05,'StartDate',today,'EndDate',datemnth(today,60));
IS = instswap([.02 .03],today,datemnth(today,60),[], [], [], [1 1]);
VolSpec = bdtvolspec(today,datemnth(today,[10 60]),[.01 .02]);
TimeSpec = bdttimespec(today,cfdates(today,datemnth(today,60),1));
BDTTree = bdttree(VolSpec,RateSpec,TimeSpec);
bdtprice(BDTTree,IS)
ans = -4.3220

Использование instswap чтобы создать несколько свопов и оценить свопы с bdtprice.

RateSpec = intenvset('Rates',.05,'StartDate',today,'EndDate',datemnth(today,60));
IS = instswap([.03 .02],today,datemnth(today,60),[], [], [], [1 1]);
IS = instswap(IS,[200 300],today,datemnth(today,60),[], [], [], [0 0]);
IS = instswap(IS,[.08 300],today,datemnth(today,60),[], [], [], [1 0]);
VolSpec = bdtvolspec(today,datemnth(today,[10 60]),[.01 .02]);
TimeSpec = bdttimespec(today,cfdates(today,datemnth(today,60),1));
BDTTree = bdttree(VolSpec,RateSpec,TimeSpec);
bdtprice(BDTTree,IS)

ans =

    4.3220
   -4.3220
   -0.2701

Входные параметры

свернуть все

Древовидная структура процентной ставки, заданная при помощи bdttree.

Типы данных: struct

Переменная инструмента, содержащая набор NINST приборы, заданные с помощью instadd. Инструменты классифицируются по типам; каждый тип может иметь различные поля данных. Сохраненное поле данных является вектором-строкой или вектором символов для каждого инструмента.

Типы данных: struct

(Необязательно) структура опций калькуляции производных, созданная с помощью derivset.

Типы данных: struct

Выходные аргументы

свернуть все

Цена для каждого прибора в момент 0, возвращенная как NINST-by- 1 вектор. Цены вычисляются путем обратного динамического программирования в дереве процентных ставок. Если инструмент не может быть оценен, NaN возвращается в эту запись.

Связанными однотипными функциями ценообразования являются:

  • bondbybdt - Цена облигации из дерева BDT.

  • capbybdt - Цена за шапку из дерева BDT.

  • cfbybdt - Цена произвольного набора денежных потоков из дерева BDT.

  • fixedbybdt - Цените примечание с фиксированной ставкой из дерева BDT.

  • floatbybdt - Цена примечания с плавающей ставкой из дерева BDT.

  • floorbybdt - Цена этажа из дерева BDT.

  • optbndbybdt - Цена опции облигации из дерева BDT.

  • optfloatbybdt - Цена примечания с плавающей ставкой с опцией из дерева BDT.

  • optemfloatbybdt - Оцените примечание с плавающей скоростью со встроенной опцией из дерева BDT.

  • optembndbybdt - Цена облигации со встроенной опцией с помощью дерева BDT.

  • rangefloatbybdt - Ценовая область значений с плавающей запятой с помощью дерева BDT.

  • swapbybdt - Цена свопа из дерева BDT.

  • swaptionbybdt - Цена свопциона из дерева BDT.

Древовидная структура цен на приборы, возвращенная как MATLAB® структура деревьев, содержащих векторы цен приборов и накопленных процентов, и вектор времени наблюдения для каждого узла. Внутри PriceTree:

  • PriceTree.PTree содержит чистые цены.

  • PriceTree.AITree содержит начисленные проценты.

  • PriceTree.tObs содержит время наблюдения.

См. также

| | | |

Темы

Представлено до R2006a

Документация по продукту Financial Instruments Toolbox

Поддержка