Основной целью выбора модели является выбор наиболее экономной модели, которая адекватно соответствует вашим данным. Три асимптотически эквивалентных теста сравнивают ограниченную модель (нулевую модель) с неограниченной моделью (альтернативная модель), соответствующей тем же данным:
Тест отношения правдоподобия (LR)
Тест множителя лагранжа (LM)
Испытание Wald (W)
Для модели с параметрами startрассмотрим ограничение 0, которое удовлетворяется нулевой моделью. Например, рассмотрите возможность проверки нулевой Функция ограничения для этого теста
Тесты LR, LM и Wald подходят к проблеме сравнения соответствия ограниченной модели неограниченной модели по-разному. Для данного набора данных пусть ) обозначает функцию логарифмирования, оцениваемую при оценке максимального правдоподобия (MLE) ограниченной (нулевой) модели. Пусть startAMLE) обозначает функцию средства к существованию, оцениваемую в MLE неограниченной (альтернативной) модели. Следующий рисунок иллюстрирует обоснование каждого теста.
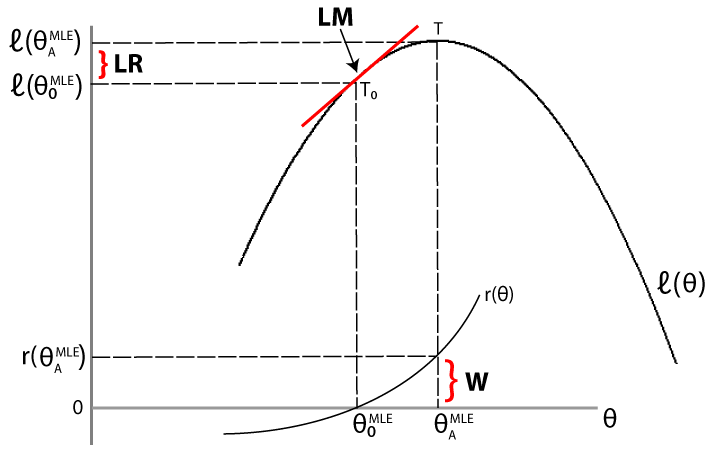
Тест отношения правдоподобия. Если ограниченная модель адекватна, то разница между максимизированными объективными функциями, start0MLE), не должна существенно отличаться от нуля.
Тест множителя Лагранжа. Если ограниченная модель адекватна, то наклон тангенса функции средства к существованию в ограниченной MLE (обозначенной T0 на рисунке) не должен значительно отличаться от нуля (который является наклоном тангенса функции средства к существованию в неограниченной MLE, обозначенной T).
Тест Уолда. Если ограниченная модель адекватна, то функция ограничения, оцененная в неограниченном MLE, не должна существенно отличаться от нуля (что является значением функции ограничения в ограниченном MLE).
Три теста асимптотически эквивалентны. При нулевом значении статистика LR, LM и Wald-теста распределяются в виде, степенями свободы, равными числу ограничений. Если проверочная статистика превышает проверочное критическое значение (эквивалентно, p-значение меньше или равно уровню значимости), нулевая гипотеза отвергается. То есть ограниченная модель отклоняется в пользу неограниченной модели.
Выбор среди тестов LR, LM и Wald в значительной степени определяется вычислительной стоимостью:
Для проведения теста отношения правдоподобия необходимо оценить как ограниченную, так и неограниченную модели.
Для проведения теста множителя Лагранжа необходимо только оценить ограниченную модель (но тест требует оценки матрицы дисперсии-ковариации).
Для проведения теста Вальда необходимо только оценить неограниченную модель (но тест требует оценки матрицы дисперсии-ковариации).
При всех равных условиях LR-тест часто является предпочтительным выбором для сравнения вложенных моделей. Econometrics Toolbox™ имеет функциональные возможности для всех трех тестов.
Можно провести тест отношения правдоподобия с помощью lratiotest. Требуемые входные данные:
Ценность максимизируемого неограниченного loglikelihood, )
Стоимость максимизированных ограниченных средств к существованию, )
Количество ограничений (степени свободы)
Учитывая эти входные данные, статистика теста отношения правдоподобия равна
start0MLE)].
При оценке моделей условного среднего и дисперсии (с использованием arima, garch, egarch, или gjr), вы можете возвратить значение целевой функции loglikeability в качестве необязательного выходного аргумента estimate или infer. Для многомерных моделей временных рядов можно получить значение целевой функции loglikeability с помощью estimate.
Для проведения теста множителя Лагранжа требуются следующие входные данные:
Градиент неограниченной вероятности, оцененный в ограниченных MLE (балл), S
Матрица дисперсии-ковариации для неограниченных параметров, оцениваемых в ограниченных MLE, V
Учитывая эти входные данные, статистика теста LM равна
Тест LM можно выполнить с помощью lmtest. Конкретным примером теста LM является тест Engle ARCH, который можно провести с помощью archtest.
Для проведения теста Вальда требуются следующие входные данные:
Функция ограничения оценивается в неограниченном MLE, r
Якобян функции ограничения, оцененной в неограниченных MLE, R
Матрица дисперсии-ковариации для неограниченных параметров, оцениваемых в неограниченных MLE, V
Учитывая эти входные данные, статистика теста для теста Вальда равна
) − 1r.
Можно провести тест Wald с помощью waldtest.
Совет
Часто можно вычислить якобиан функции ограничения аналитически. Или, при наличии символьных математических Toolbox™, можно использовать функцию jacobian.
Для оценки матрицы дисперсии-ковариации существует несколько общих методов, включая:
Внешнее произведение градиентов (OPG). Пусть G - матрица градиентов функции логарифмирования. Если набор данных имеет N наблюдений, и в неограниченном правдоподобии есть m параметров, то G является матрицей N × m.
Матрица 1 является OPG-оценкой матрицы дисперсии-ковариации.
Для arima, garch, egarch, и gjr модели, estimate метод возвращает оценку OPG матрицы дисперсии-ковариации.
Обратный отрицательный гессен (INH). При условии, что функция логарифмирования , оценка ковариации INH имеет элементы
∂θi∂θj) − 1.
Функция оценки для многомерных моделей, estimateвозвращает ожидаемую матрицу дисперсии-ковариации Гессена.
Совет
При наличии инструментария символьной математики можно использовать jacobian дважды, чтобы вычислить матрицу Гессена для вашей функции средств к существованию.
lmtest | lratiotest | waldtest