Создание регрессионных моделей с ошибками ARIMA

Модель регрессии по умолчанию со спецификациями ошибок ARIMA

Регрессионные модели с ошибками ARIMA имеют следующий вид (в нотации оператора запаздывания):

$\begin{matrix} _{yt} = c_{} +_{} \\ Xtβ + uta {(L) A}^{} (L)^{(} 1_{-} L) D (1 -_{} \end{matrix}$ Ls) ut = b (L) B (L) αt,

где

t = 1,...,T.
_yt - серия ответов.
_Xt - строка t X, которая является матрицей векторов данных конкатенированного предиктора. То есть _Xt - это наблюдение t каждой серии предикторов.
c - перехват регрессионной модели.
β - коэффициент регрессии.
_ut - серия возмущений.
_{δ t} - серия инноваций.
$^{}_{Ljyt} =_{yt}$ − j.
$a (L) = (_{1} - a1L_{-} .^{.} .$ − apLp), который является степенью p, несезонным авторегрессионным многочленом.
$A (L) = (_{1} - A1L_{-_{.}} .^{._{}} -$ ApsLps), что является _{степенью} ps, сезонным авторегрессионным многочленом.
${(1 -}^{L})$ D, который представляет собой степень D, несезонный полином интегрирования.
$(1 -^{} Ls$ ), который представляет собой степень s, сезонный полином интегрирования.
$b (L) = (_{1} + b1L_{+} .^{.} .$ + bqLq), который является степенью q, несезонным скользящим средним многочленом.
$B (L) = (_{1} + B1L_{+_{.}} .^{._{}} +$ BqsLqs), который является _{степенью} qs, сезонным скользящим средним многочленом.

Для простоты используйте сокращенную нотацию Mdl = regARIMA(p,D,q) задание регрессионной модели с ошибками ARIMA (p, D, q), гдеp, D, и q являются неотрицательными целыми числами. Mdl имеет следующие свойства по умолчанию.

Имя свойства	Тип данных свойства
`AR`	Длина `p` клеточный вектор `NaN`s
`Beta`	Пустой вектор `[]` коэффициентов регрессии, соответствующих ряду предикторов
`D`	Неотрицательный скаляр, соответствующий D
`Distribution`	`"Gaussian"`, соответствующее распределению _αt
`Intercept`	`NaN`, соответствующее c
`MA`	Длина `q` клеточный вектор `NaN`s
`P`	Количество терминов AR плюс степень интеграции, p + D
`Q`	Количество терминов MA, q
`SAR`	Пустой вектор ячейки
`SMA`	Пустой вектор ячейки
`Variance`	`NaN`, что соответствует дисперсии
`Seasonality`	`0`, соответствующее s

Если указать несезонные ошибки ARIMA, то

Свойства D и Q являются входами D и qсоответственно.
Собственность P = p + D, которая представляет собой степень соединения, несезонный авторегрессионный полином. Другими словами, P - степень произведения несезонного авторегрессивного полинома, a (L) и несезонного полинома интегрирования, (1 - L⁾ D.

Значения свойств P и Q укажите, сколько предварительных наблюдений требуется программе для инициализации временного ряда.

Можно изменить свойства Mdl с использованием точечной нотации. Например, Mdl.Variance = 0.5 устанавливает дисперсию нововведения равной 0,5.

Для максимальной гибкости при задании регрессионной модели с ошибками ARIMA используйте аргументы пары имя-значение, чтобы, например, задать каждому из авторегрессионных параметров значение или указать мультипликативные сезонные термины. Например, Mdl = regARIMA('AR',{0.2 0.1}) определяет регрессионную модель с ошибками AR (2), а коэффициенты a1 = 0,2 и _a2 = 0,1.

Укажите модели regARIMA, используя аргументы пары «имя-значение»

Можно задать только несезонные степени авторегрессии и скользящего среднего полинома, а также степень несезонного интегрирования с помощью сокращенной нотации. regARIMA(p,D,q). Некоторые задачи, такие как прогнозирование и моделирование, требуют указания значений параметров. Невозможно задать значения параметров с помощью сокращенной нотации. Для обеспечения максимальной гибкости используйте аргументы пары «имя-значение» для задания регрессионных моделей с ошибками ARIMA.

Несезонная модель ошибок ARIMA может содержать следующие многочлены:

Авторегрессивный многочлен степени p a (L) = 1 - _a1L - _a2L2 -... - ^apLp. Собственные значения a (L) должны лежать в пределах единичной окружности (т.е. a (L) должен быть стабильным многочленом).
Степень q скользящего среднего многочлена b (L) = 1 + _b1L + _b2L2 +... + ^bqLq. Собственные значения b (L) должны лежать в пределах единичной окружности (т.е. b (L) должен быть обратимым многочленом).
Многочлен несезонного интегрирования степени D равен (1 - L) D.

Следующая таблица содержит аргументы пары имя-значение, которые используются для указания модели ошибок ARIMA (т.е. регрессионной модели с ошибками ARIMA, но без компонента регрессии и перехвата):

\begin{matrix} _{yt} =_{} \\ uta (^{L) (1} - L)_{D} \end{matrix}

= b (L) αt.

(1)

Аргументы пары «имя-значение» для несезонных моделей ошибок ARIMA

Имя	Соответствующий модельный член (ы) в уравнении 1	Когда указывать
`AR`	Несезонные коэффициенты AR: a1, a2,..., _ap	Установка ограничений равенства для коэффициентов AR. Например, чтобы задать коэффициенты AR в модели ошибок ARIMA $_{ut} = 0_{.} 8ut − 1_{-} 0_{.}$ 2ut − 2 + αt, определить `'AR',{0.8,-0.2}`. Необходимо указать только ненулевые элементы `AR`. Если ненулевые коэффициенты имеют несоответствующие запаздывания, укажите соответствующие запаздывания с помощью `ARLags`. Коэффициенты должны соответствовать стабильному многочлену AR.
`ARLags`	Задержки, соответствующие ненулевым, несезонным коэффициентам AR	`ARLags` не является свойством модели. Использовать этот аргумент в качестве ярлыка для указания `AR` когда ненулевые коэффициенты AR соответствуют несектутивным запаздываниям. Например, чтобы задать ненулевые коэффициенты AR на лагах 1 и 12, например, $_{ut} =_{}_{a1ut} -_{} 1_{+}_{a2ut}$ − 12 + αt, определить `'ARLags',[1,12]`. Использовать `AR` и `ARLags` совместно для определения известных ненулевых коэффициентов AR при несектутивных лагах. Например, если в данной модели ошибок AR (12) с _a1 = 0,6 и _a12 = -0,3, укажите `'AR',{0.6,-0.3},'ARLags',[1,12]`.
`D`	Степень несезонной дифференциации, D	Задание степени несезонной разностности больше нуля. Например, чтобы задать одну степень разностности, укажите `'D',1`. По умолчанию `D` имеет значение `0` (означает отсутствие несезонной интеграции).
`Distribution`	Распределение инновационного процесса, _αt	Используйте этот аргумент, чтобы указать распределение Student's t. По умолчанию распределение инноваций `"Gaussian"`. Например, чтобы задать распределение t с неизвестными степенями свободы, укажите `'Distribution','t'`. Чтобы задать распределение инноваций с известными степенями свободы, назначьте `Distribution` структура с полями `Name` и `DoF`. Например, для распределения t с девятью степенями свободы укажите `'Distribution',struct('Name','t','DoF',9)`.
`MA`	Несезонные коэффициенты MA: b1, b2,..., _bq	Установка ограничений равенства для коэффициентов МА. Например, чтобы задать коэффициенты MA в модели ошибок ARIMA $_{ut} =_{} δ t +_{0 .} 5xpt -_{1} +$ 0 .2αt − 2, определить `'MA',{0.5,0.2}`. Необходимо указать только ненулевые элементы `MA`. Если ненулевые коэффициенты имеют несоответствующие запаздывания, укажите соответствующие запаздывания с помощью `MALags`. Коэффициенты должны соответствовать обратимому многочлену МА.
`MALags`	Задержки, соответствующие ненулевым, несезонным коэффициентам МА	`MALags` не является свойством модели. Использовать этот аргумент в качестве ярлыка для указания `MA` когда ненулевые коэффициенты МА соответствуют несектутивным запаздываниям. Например, чтобы задать ненулевые коэффициенты МА на лагах 1 и 4, например, $_{ut} =_{} {αt}_{} +_{} {b1αt}_{} -_{1} +$ b4αt − 4, определить `'MALags',[1,4]`. Использовать `MA` и `MALags` совместно для определения известных ненулевых коэффициентов МА при несектутивных лагах. Например, если в данной модели ошибок MA (4) _b1 = 0,5 и _b4 = 0,2, укажите`'MA',{0.4,0.2},'MALags',[1,4]`.
`Variance`	Скалярная дисперсия, start2, инновационного процесса, _αt	Установка зависимостей равенства для «» «» «» «» «» «» ««» Например, для модели ошибок ARIMA с известной дисперсией инноваций 0.1 укажите `'Variance',0.1`. По умолчанию `Variance` имеет значение `NaN`.

Используйте аргументы пары имя-значение в следующей таблице совместно с аргументами пары имя-значение для несезонных моделей ошибок ARIMA, чтобы указать регрессионные компоненты регрессионной модели с ошибками ARIMA.

\begin{matrix} _{yt} = c_{} +_{} \\ Xtβ +^{uta (L}) (1 -_{} L \end{matrix}

) D = b (L) αt.

(2)

Аргументы пары «имя-значение» для регрессионного компонента модели regARIMA

Имя	Соответствующий модельный член (ы) в уравнении 2	Когда указывать
`Beta`	Значения коэффициента регрессии, соответствующие серии предикторов, β	Этот аргумент используется для задания значений коэффициентов ряда предикторов. Например, использовать `'Beta',[0.5 7 -2]` определить ${\begin{matrix} \end{matrix}}^{} β=[0.57-2]'.$ По умолчанию `Beta` - пустой вектор, `[]`.
`Intercept`	Термин перехвата для регрессионной модели, c	Чтобы задать ограничения равенства для c. Например, для модели без элемента пересечения укажите `'Intercept',0`. По умолчанию `Intercept` имеет значение `NaN`.

Если временной ряд имеет сезонность s, то

Сезонный авторегрессивный многочлен степени _ps равен A (L) = 1 - A 1L - A2L2 -... - ApsLps.
Степень _qs сезонного скользящего среднего полинома - B (L) 1 + B 1L + B2L2 +... + BqsLqs.
Сезонный полином интегрирования степени s равен (1 - ^Ls).

Чтобы задать модель регрессии с мультипликативными сезонными ошибками ARIMA, используйте аргументы пары имя-значение в следующей таблице совместно с аргументами в таблицах Аргументы пары имя-значение для несезонных моделей ошибок ARIMA и Аргументы пары имя-значение для компонента регрессии модели regARIMA:

\begin{matrix} _{yt} = c_{} +_{} \\ Xtβ +^{uta (L}) (1 − L^{)}_{DA} (L) (1 -_{} Ls \end{matrix}

) ut = b (L) B (L) αt.

(3)

Аргументы пары «имя-значение» для сезонных моделей ARIMA

Аргумент	Соответствующий модельный член (ы) в уравнении 3	Когда указывать
`SAR`	Сезонные коэффициенты AR: A1, A2,...,Aps	Установка ограничений равенства для сезонных коэффициентов AR. Использовать `SARLags` для указания лагов ненулевых сезонных коэффициентов AR. Укажите задержки, связанные с сезонными многочленами в периодичности наблюдаемых данных (например, 4, 8,... для квартальных данных, или 12, 24,... для ежемесячных данных), а не кратно сезонности (например, 1, 2,...). Например, для задания модели ошибок ARIMA $(1 − 0 . 8L) (1^{−} 0_{.}_{} 2L12$ ) ut = αt, определить `'AR',0.8,'SAR',0.2,'SARLags',12`. Коэффициенты должны соответствовать стабильному сезонному многочлену AR.
`SARLags`	Задержки, соответствующие ненулевым сезонным коэффициентам AR, в периодичности ответов	`SARLags` не является свойством модели. Использовать этот аргумент при указании `SAR` для указания лагов ненулевых сезонных коэффициентов AR. Например, для задания модели ошибок ARIMA $(1 -_{} a1L) (_{1} -^{}_{} {A12L12}_{)}$ ut = αt, определить `'ARLags',1,'SARLags',12`.
`SMA`	Сезонные коэффициенты MA: B1, B2,...,Bqs	Установка ограничений равенства для сезонных коэффициентов МА. Использовать `SMALags` для задания лагов ненулевых сезонных коэффициентов МА. Укажите задержки, связанные с сезонными многочленами в периодичности наблюдаемых данных (например, 4, 8,... для квартальных данных, или 12, 24,... для ежемесячных данных), а не кратно сезонности (например, 1, 2,...). Например, для задания модели ошибок ARIMA $_{ut} = (1 + 0 . 6L) (^{1} +_{} 0$ .2L4) αt, определить `'MA',0.6,'SMA',0.2,'SMALags',4`. Коэффициенты должны соответствовать обратимому сезонному многочлену МА.
`SMALags`	Задержки, соответствующие ненулевым сезонным коэффициентам МА, в периодичности ответов	`SMALags` не является свойством модели. Использовать этот аргумент при указании `SMA` для указания лагов ненулевых сезонных коэффициентов МА. Например, для задания модели $_{ut} = (1_{} + b1L)_{} (^{1} +_{}$ B4L4) αt, определить `'MALags',1,'SMALags',4`.
`Seasonality`	Сезонная периодичность, с	Чтобы задать степень сезонного интегрирования s в сезонном разностном многочлене _Δs = 1 - ^Ls. Например, для определения периодичности сезонной интеграции квартальных данных укажите `'Seasonality',4`. По умолчанию `Seasonality` имеет значение `0` (означает отсутствие периодичности или сезонной интеграции).

Примечание

Невозможно назначить значения свойствам P и Q. Для мультипликативных моделей ошибок ARIMA

regARIMA наборы P равно p + D + _ps + s.
regARIMA наборы Q равно q + _qs

Задание моделей линейной регрессии с помощью приложения эконометрического моделирования

Вы можете указать переменные предиктора в компоненте регрессии, а также структуру запаздывания модели ошибок и распределение инноваций, используя приложение Econometric Modeler. Приложение рассматривает все коэффициенты как неизвестные и оцениваемые.

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Можно также открыть приложение из галереи приложений (см. Econometric Modeler).

В приложении можно просмотреть все поддерживаемые модели, выбрав переменную временного ряда для ответа на панели Временной ряд. Затем на вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.

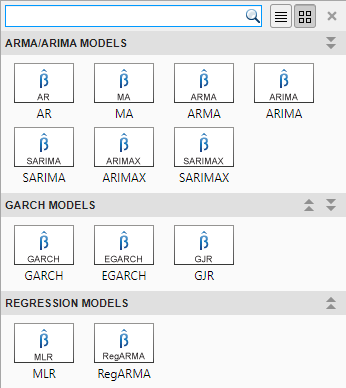
Раздел Регрессионные модели содержит поддерживаемые регрессионные модели. Чтобы задать модель множественной линейной регрессии (MLR), выберите MLR. Чтобы задать регрессионные модели с ошибками ARMA, выберите RegARMA.

После выбора модели приложение отображает Type диалоговое окно «Параметры модели», где Type - тип модели. На этом рисунке показано диалоговое окно Параметры модели RegARMA (RegARMA Model Parameters).

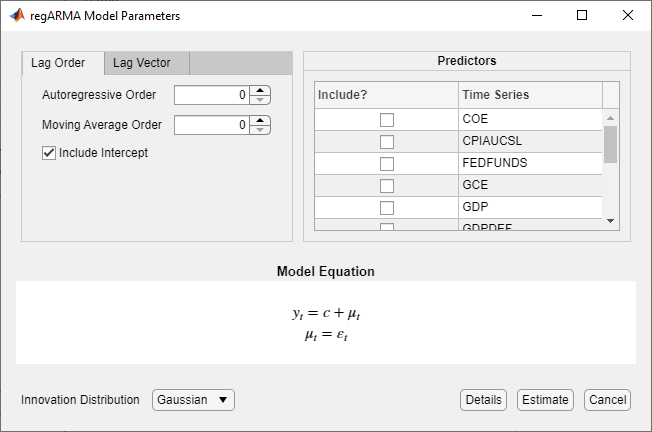
Регулируемые параметры зависят от модели Type. В целом, регулируемые параметры включают в себя:

Переменные предиктора для компонента линейной регрессии, перечисленные в разделе Предикторы.
- Для регрессионных моделей с ошибками ARMA необходимо включить в модель хотя бы один предиктор. Чтобы включить предиктор, установите соответствующий флажок в поле Включить? столбец.
- Для моделей MLR можно снять все флажки в окне Включить? столбец. В этом случае можно указать постоянную среднюю модель (модель только для перехвата), установив флажок Включить перехват (Include Intercept). Можно также указать модель только для ошибок, сняв флажок Включить перехват (Include Intercept).
Инновационное распределение и несезонные задержки для модели ошибок, для регрессионных моделей с ошибками ARMA.

При корректировке значений параметров уравнение в разделе «Уравнение модели» изменяется в соответствии со спецификациями. Регулируемые параметры соответствуют аргументам пары «вход» и «имя-значение», описанным в предыдущих разделах и в regARIMA справочная страница.

Дополнительные сведения об указании моделей с помощью приложения см. в разделах Подгонка моделей к данным и Определение многочленов оператора задержки в интерактивном режиме.