В этом примере показано применение краткого текста regARIMA(p,D,q) для задания регрессионной модели с ошибками ARMA.
Укажите модель регрессии по умолчанию с ошибками ARMA (3,2 ):
+ b1αt-1 + b2αt-2.
Mdl = regARIMA(3,0,2)
Mdl =
regARIMA with properties:
Description: "ARMA(3,2) Error Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
Intercept: NaN
Beta: [1×0]
P: 3
Q: 2
AR: {NaN NaN NaN} at lags [1 2 3]
SAR: {}
MA: {NaN NaN} at lags [1 2]
SMA: {}
Variance: NaN
Программа устанавливает для каждого параметра значение NaNи распространение инноваций в Gaussian. Коэффициенты AR находятся на лагах 1-3, а коэффициенты MA - на лагах 1 и 2.
Проход Mdl в estimate с данными для оценки параметров, установленных на NaN. regARIMA наборы моделей Beta кому [] и не отображает его. Если передать матрицу предикторов () в estimate, то estimate оценки Beta. estimate функция выводит число коэффициентов регрессии в Beta из числа столбцов в .
Такие задачи, как моделирование и прогнозирование с использованием simulate и forecast не принимать модели хотя бы с одной NaN для значения параметра. Используйте точечную нотацию для изменения значений параметров.
В этом примере показано, как указать регрессионную модель с ошибками ARMA без перехвата регрессии.
Укажите модель регрессии по умолчанию с ошибками ARMA (3,2):
b1αt-1 + b2αt-2.
Mdl = regARIMA('ARLags',1:3,'MALags',1:2,'Intercept',0)
Mdl =
regARIMA with properties:
Description: "ARMA(3,2) Error Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
Intercept: 0
Beta: [1×0]
P: 3
Q: 2
AR: {NaN NaN NaN} at lags [1 2 3]
SAR: {}
MA: {NaN NaN} at lags [1 2]
SMA: {}
Variance: NaN
Наборы программного обеспечения Intercept до 0, но все остальные параметры в Mdl являются NaN значения по умолчанию.
С тех пор Intercept не является NaN, это ограничение равенства во время оценки. Другими словами, если вы проходите Mdl и данные в estimate, то estimate наборы Intercept до 0 во время оценки.
Можно изменить свойства Mdl с использованием точечной нотации.
В этом примере показано, как указать регрессионную модель с ошибками ARMA, где ненулевые члены ARMA находятся на несектутивных лагах.
Укажите регрессионную модель с ошибками ARMA (8,4):
+ b1αt-1 + b4αt-4.
Mdl = regARIMA('ARLags',[1,4,8],'MALags',[1,4])
Mdl =
regARIMA with properties:
Description: "ARMA(8,4) Error Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
Intercept: NaN
Beta: [1×0]
P: 8
Q: 4
AR: {NaN NaN NaN} at lags [1 4 8]
SAR: {}
MA: {NaN NaN} at lags [1 4]
SMA: {}
Variance: NaN
Коэффициенты AR находятся на лагах 1, 4 и 8, а коэффициенты MA находятся на лагах 1 и 4. Программа устанавливает промежуточные задержки в 0.
Проход Mdl и данные в estimate. Программа оценивает все параметры, которые имеют значение NaN. Тогда estimate удерживает все промежуточные коэффициенты запаздывания до 0 во время оценки.
В этом примере показано, как задать значения для всех параметров регрессионной модели с ошибками ARMA.
Укажите регрессионную модель с ошибками ARMA (3,2):
0.5αt-1 + 0.2αt-2,
где - гауссова с единичной дисперсией.
Mdl = regARIMA('Intercept',0,'Beta',[2.5; -0.6],... 'AR',{0.7, -0.3, 0.1},'MA',{0.5, 0.2},'Variance',1)
Mdl =
regARIMA with properties:
Description: "Regression with ARMA(3,2) Error Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
Intercept: 0
Beta: [2.5 -0.6]
P: 3
Q: 2
AR: {0.7 -0.3 0.1} at lags [1 2 3]
SAR: {}
MA: {0.5 0.2} at lags [1 2]
SMA: {}
Variance: 1
Параметры в Mdl не содержать NaN значения, и поэтому нет необходимости оценивать Mdl использование estimate. Однако можно моделировать или прогнозировать ответы из Mdl использование simulate или forecast.
В этом примере показано, как задать для инновационного распределения регрессионной модели с ошибками ARMA распределение t.
Укажите регрессионную модель с ошибками ARMA (3,2 ):
0.5αt-1 + 0.2αt-2,
где имеет t-распределение со степенями свободы и единичной дисперсией по умолчанию.
Mdl = regARIMA('Intercept',0,'Beta',[2.5; -0.6],... 'AR',{0.7, -0.3, 0.1},'MA',{0.5, 0.2},'Variance',1,... 'Distribution','t')
Mdl =
regARIMA with properties:
Description: "Regression with ARMA(3,2) Error Model (t Distribution)"
Distribution: Name = "t", DoF = NaN
Intercept: 0
Beta: [2.5 -0.6]
P: 3
Q: 2
AR: {0.7 -0.3 0.1} at lags [1 2 3]
SAR: {}
MA: {0.5 0.2} at lags [1 2]
SMA: {}
Variance: 1
По умолчанию используются следующие степени свободы: NaN. Если вы не знаете степеней свободы, то вы можете оценить это, пройдя Mdl и данные для estimate.
Укажите распределение t5.
Mdl.Distribution = struct('Name','t','DoF',5)
Mdl =
regARIMA with properties:
Description: "Regression with ARMA(3,2) Error Model (t Distribution)"
Distribution: Name = "t", DoF = 5
Intercept: 0
Beta: [2.5 -0.6]
P: 3
Q: 2
AR: {0.7 -0.3 0.1} at lags [1 2 3]
SAR: {}
MA: {0.5 0.2} at lags [1 2]
SMA: {}
Variance: 1
Можно моделировать или прогнозировать ответы из Mdl использование simulate или forecast потому что Mdl полностью указан.
В приложениях, таких как моделирование, программное обеспечение нормализует случайные t инноваций. Другими словами, Variance переопределяет теоретическую дисперсию t случайной величины (которая DoF/(DoF - 2)), но сохраняет куртоз распределения.
В приложении Econometric Modeler можно указать переменные предиктора в компоненте регрессии, а также структуру запаздывания модели ошибок и распределение инноваций регрессионной модели с ошибками ARMA (p, q), выполнив следующие шаги. Все указанные коэффициенты неизвестны, но поддаются оценке.
В командной строке откройте приложение Econometric Modeler.
econometricModeler
Можно также открыть приложение из галереи приложений (см. Econometric Modeler).
На панели Временной ряд (Time Series) выберите временной ряд ответа, по которому будет соответствовать модель.
На вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.
В коллекции моделей в разделе Регрессионные модели щелкните РегАРМА.
Откроется диалоговое окно Параметры модели RegARMA (RegARMA Model Parameters).
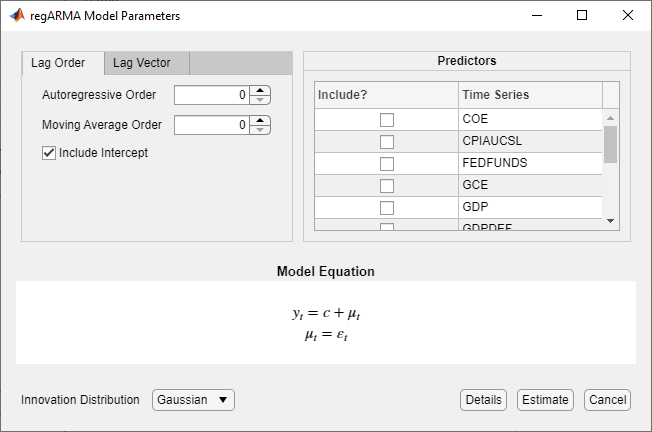
Выберите структуру задержки модели ошибок. Чтобы указать регрессионную модель с ошибками ARMA (p, q), которая включает все задержки AR от 1 до p и все задержки MA от 1 до q, используйте вкладку Порядок задержки (Lag Order). Для обеспечения гибкости при определении включения определенных лагов используйте вкладку Вектор лага (Lag Vector). Дополнительные сведения см. в разделе Интерактивное определение многочленов оператора задержки. Независимо от используемой вкладки можно проверить форму модели, проверив уравнение в разделе «Уравнение модели».
В разделе Предикторы выберите хотя бы одну переменную предиктора, выбрав Включить? флажок для временного ряда.
Например, предположим, что вы работаете с Data_USEconModel.mat набор данных и его переменные перечислены на панели «Временной ряд».
Чтобы указать регрессионную модель с ошибками AR (3) для уровня безработицы, содержащего все последовательные задержки AR от 1 через ее порядок, гауссово-распределенные инновации и переменные-предикторы COE, CPIAUCSL, FEDFUNDS и ВВП:
На панели «Временной ряд» выберите UNRATE временные ряды.
На вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.
В коллекции моделей в разделе Регрессионные модели щелкните РегАРМА.
.
В диалоговом окне «Параметры модели regARMA» на вкладке «Порядок задержки» установите для параметра «Порядок авторегрессии» значение 3.
В разделе Предикторы выберите Включить? флажок для временных рядов COE, CPIAUCSL, FEDFUNDS и ВВП.
Чтобы указать регрессионную модель с ошибками MA (2) для уровня безработицы, содержащего все MA, отстает от 1 по своему порядку, гауссово-распределенные инновации и предикторные переменные COE и CPIAUCSL.
На панели «Временной ряд» выберите UNRATE временные ряды.
На вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.
В коллекции моделей в разделе Регрессионные модели щелкните РегАРМА.
В диалоговом окне «Параметры модели regARMA» на вкладке «Порядок задержки» задайте для параметра «Порядок скользящего среднего» значение 2.
В разделе Предикторы выберите Включить? флажок для временных рядов COE и CPIAUCSL.
Определение регрессионной модели с ошибками ARMA (8,4) для уровня безработицы, содержащей несектутивные задержки
= (1 + b1L + b4L4) αt,
где αt - серия гауссовых инноваций IID:
На панели «Временной ряд» выберите UNRATE временные ряды.
На вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.
В коллекции моделей в разделе Регрессионные модели щелкните РегАРМА.
В диалоговом окне «Параметры модели regARMA» перейдите на вкладку «Вектор задержки»:
В поле «Авторегрессионные задержки» введите 1 4 8.
В поле «Задержки скользящего среднего» введите 1 4.
В разделе Предикторы выберите Включить? флажок для временных рядов COE и CPIAUCSL.
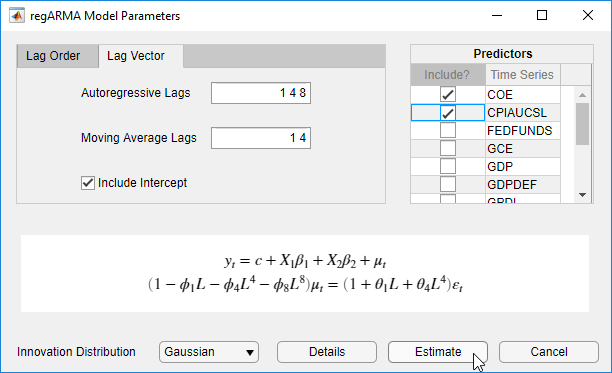
Чтобы указать регрессионную модель с ошибками ARMA (3,2) для уровня безработицы, содержащего все последовательные задержки AR и MA через их соответствующие порядки, переменные предиктора COE и CPIAUCSL и t-распределенные инновации:
На панели «Временной ряд» выберите UNRATE временные ряды.
На вкладке Эконометрический моделирующий (Econometric Modeler) в разделе Модели (Models) щелкните стрелку, чтобы отобразить галерею моделей.
В коллекции моделей в разделе Регрессионные модели щелкните РегАРМА.
В диалоговом окне «Параметры модели regARMA» перейдите на вкладку «Порядок задержки»:
Задать авторегрессионный порядок как 3.
Задайте для заказа скользящего среднего значение 2.
Нажмите кнопку Распределение инноваций и выберите t.
В разделе Предикторы выберите Включить? флажок для временных рядов COE и CPIAUCSL.
Параметр степеней свободы распределения t является неизвестным, но оцениваемым параметром.
После задания модели щелкните Оценка (Estimate), чтобы оценить все неизвестные параметры в модели.