Вычислите выход, ошибку и веса адаптивного фильтра LMS
The dsp.LMSFilter Система object™ реализует адаптивный фильтр с конечной импульсной характеристикой (КИХ), который сходит входной сигнал к желаемому сигналу с помощью одного из следующих алгоритмов:
LMS
Нормированная LMS
Sign-Data LMS
Sign-Error LMS
Sign-Sign LMS
Для получения дополнительной информации о каждом из этих методов, см. Алгоритмы.
Фильтр адаптирует свои веса до тех пор, пока ошибка между основным входным сигналом и желаемым сигналом не будет минимальной. Средний квадрат этой ошибки (MSE) вычисляется с помощью msesim функция. Предсказанная версия MSE определяется с использованием фильтра Винера в msepred функция. maxstep функция вычисляет максимальный размер шага адаптации, который управляет скоростью сходимости.
Обзор методологии адаптивного фильтра и наиболее распространенных приложений, в которых используются адаптивные фильтры, см. в разделе Обзор адаптивных фильтров и приложений.
Для фильтрации сигнала с помощью адаптивного конечная импульсная характеристика:
Создайте dsp.LMSFilter Объекту и установите его свойства.
Вызывайте объект с аргументами, как будто это функция.
Дополнительные сведения о работе системных объектов см. в разделе «Что такое системные объекты?».
При определенных условиях этот системный объект также поддерживает генерацию кода SIMD. Для получения дополнительной информации смотрите Генерация кода.
lms = dsp.LMSFilterlms, который вычисляет отфильтрованный выход, ошибку фильтра и веса фильтра для данного входного сигнала и желаемого сигнала, используя алгоритм наименьших средних квадратов (LMS).
lms = dsp.LMSFilter( возвращает объект фильтра LMS с каждым заданным набором свойств заданное значение. Заключайте каждое имя свойства в одинарные кавычки. Можно использовать этот синтаксис с предыдущим входным параметром.Name,Value)
Если не указано иное, свойства являются нетронутыми, что означает, что вы не можете изменить их значения после вызова объекта. Объекты блокируются, когда вы вызываете их, и release функция разблокирует их.
Если свойство настраивается, можно изменить его значение в любой момент.
Для получения дополнительной информации об изменении значений свойств смотрите Разработку системы в MATLAB Использование Системных объектов.
Method - Метод вычисления весов фильтров'LMS' (по умолчанию) | 'Normalized LMS' | 'Sign-Data LMS' | 'Sign-Error LMS' | 'Sign-Sign LMS'Метод вычисления весов фильтра, заданный как один из следующих:
'LMS' - Решает уравнение Вайнера-Хопфа и находит коэффициенты фильтра для адаптивного фильтра.
'Normalized LMS' - Нормализованное изменение LMS-алгоритма.
'Sign-Data LMS' - Коррекция к весам фильтра при каждой итерации зависит от знака входа x.
'Sign-Error LMS' - Коррекция, применяемая к текущим весам фильтра для каждой последующей итерации, зависит от знака ошибки err.
'Sign-Sign LMS' - Коррекция, применяемая к текущим весам фильтра для каждой последующей итерации, зависит от обоих признаков x и знак err.
Для получения дополнительной информации об алгоритмах см. «Алгоритмы».
Length - Длина вектора весов конечной импульсной характеристики32 (по умолчанию) | положительное целое числоДлина вектора весов конечной импульсной характеристики, заданная как положительное целое число.
Пример: 64
Пример: 16
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
StepSizeSource - Метод для определения размера шага адаптации'Property' (по умолчанию) | 'Input port'Метод для определения размера шага адаптации, заданный как один из следующих:
'Property' - Свойство StepSize задает размер каждого шага адаптации.
'Input port' - Задайте размер шага адаптации как один из входов для объекта.
StepSize - Размер шага адаптации0.1 (по умолчанию) | неотрицательный скалярКоэффициент размера шага адаптации, заданный как неотрицательный скаляр. Для сходимости нормализованного метода LMS, размер шага должен быть больше 0 и меньше 2.
Небольшой шаг обеспечивает небольшую ошибку устойчивого состояния между выходом y и желаемым сигналом d. Если размер шага невелик, скорость сходимости фильтра уменьшается. Чтобы улучшить скорость сходимости, увеличьте размер шага. Обратите внимание, что если размер шага велик, фильтр может стать нестабильным. Чтобы вычислить максимальный размер шага, который фильтр может принять, не становясь нестабильным, используйте maxstep функция.
Настраиваемый: Да
Это свойство применяется, когда вы задаете StepSizeSource равным 'Property'.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
LeakageFactor - Коэффициент утечки, используемый в утечечном методе LMS1 (по умолчанию) | [0 1]Коэффициент утечки, используемый при реализации метода утечки LMS, заданный как скаляр в области значений [0 1]. Когда значение равняется 1, в способе адаптации нет утечек. Когда значение меньше 1, фильтр реализует метод утечки LMS.
Пример: 0.5
Настраиваемый: Да
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
InitialConditions - Начальные условия весов фильтров0 (по умолчанию) | скалярный вектор |Начальные условия весов фильтра, заданные как скаляр или вектор длины, равной значению свойства Length. Когда вход действителен, значение этого свойства должно быть реальным.
Пример: 0
Пример: [1 3 1 2 7 8 9 0 2 2 8 2]
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Поддержка комплексного числа: Да
AdaptInputPort - Флаг для адаптации весов фильтровfalse (по умолчанию) | trueФлаг для адаптации весов фильтра, заданный как один из следующих:
false - Объект постоянно обновляет веса фильтров.
true - Вход управления адаптацией предоставляется объекту, когда вы вызываете его алгоритм. Если значение этого входа ненулевое, объект постоянно обновляет веса фильтров. Если значение этого входа меньше нуля, веса фильтров остаются на своем текущем значении.
WeightsResetInputPort - Флаг для сброса весов фильтраfalse (по умолчанию) | trueФлаг для сброса весов фильтра, заданный как один из следующих:
false - Объект не сбрасывает веса.
true - Вход управления сбросом предоставляется объекту, когда вы вызываете его алгоритм. Этот параметр включает свойство WeightsResetCondition. Объект сбрасывает веса фильтра на основе значений WeightsResetCondition свойство и вход сброса, предоставленный алгоритму объекта.
WeightsResetCondition - Событие для сброса весов фильтра'Non-zero' (по умолчанию) | 'Rising edge' | 'Falling edge' | 'Either edge'Событие, которое инициирует сброс весов фильтра, заданный как одно из следующих. Объект сбрасывает веса фильтра всякий раз, когда событие сброса обнаруживается на его входе сброса.
'Non-zero' -- Запускает операцию сброса на каждой выборке, когда вход сброса не равен нулю.
'Rising edge' -- Запускает операцию сброса, когда вход сброса делает одно из следующего:
Повышается с отрицательного значения до положительного значения или нуля.
Поднимается с нуля до положительного значения, где подъем не является продолжением подъёма с отрицательного значения до нуля.
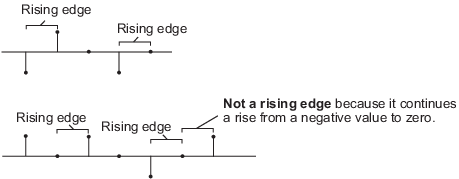
'Falling edge' -- Запускает операцию сброса, когда вход сброса делает одно из следующего:
Падает от положительного значения до отрицательного значения или нуля.
Падает с нуля до отрицательного значения, где падение не является продолжением падения с положительного значения до нуля.
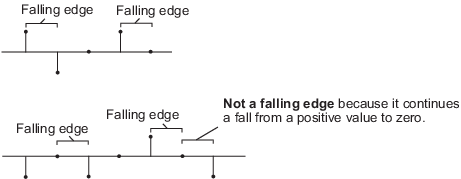
'Either edge' -- Запускает операцию сброса, когда вход сброса является восходящим ребром или падающим ребром.
Объект сбрасывает веса фильтра на основе значения этого свойства и входных параметров сброса r предоставляется алгоритму объекта.
Это свойство применяется, когда вы задаете значение свойства WeightsResetInportPort true.
WeightsOutput - Метод вывода адаптированных весов фильтра'Last' (по умолчанию) | 'None' | 'All'Метод вывода адаптированных весов фильтра, заданный как одно из следующего:
'Last' (по умолчанию) - объект возвращает вектор-столбец весов, соответствующий последней выборке системы координат данных. Длина вектора весов является значением, заданным свойством Length.
'All' - Объект возвращает FrameLength -by - Length матрицу весов. Матрица соответствует полной истории весов по выборкам для всех FrameLength выборок входных значений. Каждая строка в матрице соответствует набору весов фильтра LMS, вычисленных для соответствующей входной выборки.
'None' - Этот параметр отключает выход весов.
RoundingMethod - Метод округления для операций с фиксированной точкой'Floor' (по умолчанию) | 'Ceiling' | 'Convergent' | 'Nearest' | 'Round' | 'Simplest' | 'Zero'Задайте режим округления для операций с фиксированной точкой. Для получения дополнительной информации смотрите режим округления.
OverflowAction - Действие переполнения для операций с фиксированной точкой'Wrap' (по умолчанию) | 'Saturate'Действие переполнения для операций с фиксированной точкой, заданное как одно из следующего:
'Wrap' - Объект переносит результат своих операций с фиксированной точкой.
'Saturate' - Объект насыщает результат своих операций с фиксированной точкой.
Для получения дополнительной информации о действиях переполнения смотрите режим переполнения для операций с фиксированной точкой.
StepSizeDataType - Настройки размера слова шага и длины дроби'Same word length as first input' (по умолчанию) | 'Custom'Настройки размера слова и длины дроби, заданные как один из следующих:
'Same word length as first input' - Объект задает, чтобы размер слова размера шага совпадал с длиной слова первого входа. Длина дроби вычисляется, чтобы получить лучшую возможную точность.
'Custom' - Тип данных размера шага задается как пользовательский числовой тип через свойство CustomStepSizeDataType.
Дополнительные сведения о типе данных размера шага, используемом этим объектом, см. в разделе Фиксированная точка.
CustomStepSizeDataType - Длина слова и дроби шагаnumerictype([],16,15) (по умолчанию)Длина слова и дроби размера шага, заданная как автоматический числовой тип с размером слова 16 и длиной дроби 15.
Пример: численный тип ([], 32)
Это свойство применяется при следующих условиях:
Для набора свойств 'Property' и для параметра StepSizeDataType задано значение 'Custom'.
StepSizeSource значение свойства установлено в 'Input port'.
LeakageFactorDataType - Настройки размера слова коэффициента утечки и длины дроби'Same word length as first input' (по умолчанию) | 'Custom'Настройки размера слова коэффициента утечки и длины дроби, заданные как одно из следующего:
'Same word length as first input' - Объект задает размер слова коэффициента утечки так же, как и в первом входе. Длина дроби вычисляется, чтобы получить лучшую возможную точность.
'Custom' - Тип данных коэффициента утечки задается как пользовательский числовой тип с помощью свойства CustomLeakageFactorDataType.
Для получения дополнительной информации о типе данных коэффициента утечки, используемом этим объектом, см. раздел Фиксированная точка.
CustomLeakageFactorDataType - Длина слова и дроби коэффициента утечкиnumerictype([],16,15) (по умолчанию)Длина слова и дроби коэффициента утечки, заданная как автоматический числовой тип с размером слова 16 и длиной дроби 15.
Пример: численный тип ([], 32)
Это свойство применяется, когда вы задаете значение свойства LeakageFactorDataType 'Custom'.
WeightsDataType - Настройки размера слова и длины дроби'Same as first input' (по умолчанию) | 'Custom'Веса размера слова и настройки длины дроби, заданные как один из следующих:
'Same as first input' -- Объект задает тип данных весов фильтра таким же, как и у первого входа.
'Custom' - Тип данных весов фильтра задается как пользовательский числовой тип с помощью свойства CustomWeightsDataType.
Дополнительные сведения о типе данных весов фильтров, используемых этим объектом, см. в разделе Фиксированная точка.
CustomWeightsDataType - Длина слова и дроби фильтровnumerictype([],16,15) (по умолчанию)Длина слова и дроби весов фильтра, заданная как автоматический числовой тип с размером слова 16 и длиной дроби 15.
Пример: численный тип ([], 32,20)
Это свойство применяется, когда вы задаете значение свойства WeightsDataType 'Custom'.
EnergyProductDataType - Настройки длины и длины дроби энергетического продукта'Same as first input' (по умолчанию) | 'Custom'Настройки размера слова энергетического продукта и длины фракции, заданные как одно из следующего:
'Same as first input' - Объект задает тип данных энергетического продукта, который будет таким же, как и у первого входа.
'Custom' - Тип данных энергетического продукта задается как пользовательский числовой тип через свойство CustomEnergyProductDataType.
Для получения дополнительной информации о типе данных энергетического продукта, который используется этим объектом, смотрите раздел Фиксированная точка.
Это свойство применяется, когда вы задаете свойство Method равным 'Normalized LMS'.
CustomEnergyProductDataType - Слово и дроби энергетического продуктаnumerictype([],32,20) (по умолчанию)Длина слова и дроби энергетического продукта, заданная как автоматический числовой тип с размером слова 32 и длиной дроби 20.
Это свойство применяется, когда вы задаете свойство Method равным 'Normalized LMS' и свойство EnergyProductDataType в 'Custom'.
EnergyAccumulatorDataType - Настройки размера слова аккумулятора энергии и длины дроби'Same as first input' (по умолчанию) | 'Custom'Настройки размера слова аккумулятора энергии и длины дроби, заданные как одно из следующего:
'Same as first input' - Объект задает тип данных аккумулятора энергии таким же, как и у первого входа.
'Custom' - Тип данных аккумулятора энергии задается как пользовательский числовой тип через свойство CustomEnergyAccumulatorDataType.
Для получения дополнительной информации о типе данных аккумулятора энергии, используемом этим объектом, смотрите раздел Фиксированная точка.
Это свойство применяется, когда вы задаете свойство Method равным 'Normalized LMS'.
CustomEnergyAccumulatorDataType - Длина слова и дроби аккумулятора энергииnumerictype([],32,20) (по умолчанию)Длина слова и дроби аккумулятора энергии, заданная как автоматический числовой тип с размером слова 32 и длиной дроби 20.
Это свойство применяется, когда вы задаете свойство Method равным 'Normalized LMS' и свойство EnergyAccumulatorDataType в 'Custom'.
ConvolutionProductDataType - Настройки размера слова продукта свертки и длины дроби'Same as first input' (по умолчанию) | 'Custom'Настройки свертки продукта размера слова и длины дроби, заданные как одно из следующего:
'Same as first input' -- Объект задает тип данных продукта свертки таким же, как и у первого входа.
'Custom' - Тип данных продукта свертки задается как пользовательский числовой тип с помощью свойства CustomConvolutionProductDataType.
Для получения дополнительной информации о типе данных продукта свертки, используемом этим объектом, смотрите раздел Фиксированная точка.
CustomConvolutionProductDataType - Длина слова и дроби продуктаnumerictype([],32,20) (по умолчанию)Длина слова и дроби продукта свертки, заданная как автоматический числовой тип с размером слова 32 и длиной дроби 20.
Это свойство применяется, когда вы задаете значение свойства ConvolutionProductDataType 'Custom'.
ConvolutionAccumulatorDataType - Настройки размера слова аккумулятора свертки и длины дроби'Same as first input' (по умолчанию) | 'Custom'Настройки размера слова аккумулятора свертки и длины дроби, заданные как одно из следующего:
'Same as first input' - Объект задает тип данных аккумулятора свертки таким же, как и у первого входа.
'Custom' - Тип данных аккумулятора свертки задается как пользовательский числовой тип через свойство CustomConvolutionAccumulatorDataType.
Для получения дополнительной информации о типе данных аккумулятора свертки, используемом этим объектом, смотрите раздел «Фиксированная точка».
CustomConvolutionAccumulatorDataType - Длина слова и дроби свертки аккумулятораnumerictype([],32,20) (по умолчанию)Длина слова и дроби аккумулятора свертки, заданная как автоматический числовой тип с размером слова 32 и длиной дроби 20.
Это свойство применяется, когда вы задаете значение свойства ConvolutionAccumulatorDataType 'Custom'.
StepSizeErrorProductDataType - Ошибка размера шага: настройки размера слова продукта и длины дроби'Same as first input' (по умолчанию) | 'Custom'Размер шага ошибка продукта настройки размера слова и длины дроби, заданные как одно из следующего:
'Same as first input' -- Объект задает тип данных продукта ошибки размера шага таким же, как и при первом входе.
Для получения дополнительной информации о типе данных продукта ошибки размера шага, используемом этим объектом, смотрите раздел Фиксированная точка.
CustomStepSizeErrorProductDataType - Длина слова и дроби продукта ошибки размера шагаnumerictype([],32,20) (по умолчанию)WeightsUpdateProductDataType - Веса фильтра обновляют настройки размера слова продукта и длины дроби'Same as first input' (по умолчанию) | 'Custom'Настройки длины слова и фракции продукта обновления весов фильтра, заданные как одно из следующего:
'Same as first input' -- Объект задает тип данных продукта обновления весов фильтров таким же, как и при первом входе.
'Custom' - Тип данных продукта обновления весов фильтров задается как пользовательский числовой тип с помощью свойства CustomWeightsUpdateProductDataType.
Для получения дополнительной информации о весах фильтров, обновляющих тип данных продукта, используемый этим объектом, смотрите раздел Фиксированная точка.
CustomWeightsUpdateProductDataType - Слово и дроби весов фильтра обновляют продуктnumerictype([],32,20) (по умолчанию)Длины слова и дроби весов фильтра обновляют продукт, заданный как автоматический числовой тип с размером слова 32 и длиной дроби 20.
Это свойство применяется, когда вы задаете значение свойства WeightsUpdateProductDataType 'Custom'.
QuotientDataType - Настройки длины и длины дроби отдельного слова'Same as first input' (по умолчанию) | 'Custom'Настройки факторного размера слова и длины дроби, заданные как один из следующих:
'Same as first input' -- Объект задает тип факторных данных, который должен совпадать с типом данных первого входа.
'Custom' - Частный тип данных задается как пользовательский числовой тип с помощью свойства CustomQuotientDataType.
Дополнительные сведения о типе факторных данных, используемом этим объектом, см. в разделе Фиксированная точка.
Это свойство применяется, когда вы задаете свойство Method равным 'Normalized LMS'.
CustomQuotientDataType - Длина слова и дроби фактораnumerictype([],32,20) (по умолчанию)Длины слова и дроби весов фильтра обновляют продукт, заданный как автоматический числовой тип с размером слова 32 и длиной дроби 20.
Это свойство применяется, когда вы задаете свойство Method равным 'Normalized LMS' и свойство QuotientDataType в 'Custom'.
[ фильтрует входной сигнал, y,err,wts] = lms(x,d)x, использование d в качестве необходимого сигнала и возвращает отфильтрованный выход в y, ошибка фильтра в err, и предполагаемые веса фильтров в wts. Объект фильтра LMS оценивает веса фильтра, необходимые для минимизации ошибки между выходом сигналом и желаемым сигналом.
[ фильтрует входной сигнал, y,err] = lms(x,d)x, использование d в качестве необходимого сигнала и возвращает отфильтрованный выход в y и ошибка фильтра в err если для свойства WeightsOutput задано значение 'None'.
[___] = lms( фильтрует входной сигнал, x,d,mu)x, использование d как необходимый сигнал и mu в качестве размера шага, когда для свойства StepSizeSource задано значение 'Input port'. Эти входы могут использоваться с любым из предыдущих наборов выходов.
[___] = lms( фильтрует входной сигнал, x,d,a)x, использование d как необходимый сигнал и a как управление адаптацией, когда для свойства AdaptInportPort задано значение true. Когда a является ненулевым, системный объект постоянно обновляет веса фильтров. Когда a равен нулю, веса фильтров остаются постоянными.
[___] = lms( фильтрует входной сигнал, x,d,r)x, использование d как необходимый сигнал и r как сигнал сброса, когда для свойства WeightsResetInportPort задано значение true. Свойство WeightsResetCondition может использоваться, чтобы задать условие триггера сброса. Если происходит событие сброса, системный объект сбрасывает веса фильтров к их начальным значениям.
x - Вход данныхСигнал, который будет фильтроваться фильтром LMS. Вход, xи желаемый сигнал, d должен иметь одинаковый размер, тип и сложность данных. Если вход является фиксированной точкой, тип данных должен быть подписан и должен иметь тот же размер слова, что и требуемый сигнал.
Вход, x может быть сигналом переменного размера. Вы можете изменить количество элементов в векторе-столбце, даже когда объект заблокирован. Системный объект блокируется, когда вы вызываете объект, чтобы запустить его алгоритм.
Типы данных: single | double | int8 | int16 | int32 | int64 | fi
Поддержка комплексного числа: Да
d - Желаемый сигналФильтр LMS адаптирует свои веса фильтров, wts, чтобы минимизировать ошибку, err, и сходятся входной сигнал x к желаемому сигналу d максимально близко.
Вход, xи желаемый сигнал, d, должны иметь одинаковый размер, тип данных и сложность. Если требуемый сигнал является фиксированной точкой, тип данных должен быть подписан и должен иметь тот же размер слова, что и вход данных.
Вход, d может быть сигналом переменного размера. Вы можете изменить количество элементов в векторе-столбце, даже когда объект заблокирован. Системный объект блокируется, когда вы вызываете объект, чтобы запустить его алгоритм.
Типы данных: single | double | int8 | int16 | int32 | int64 | fi
Поддержка комплексного числа: Да
mu - Размер шагаКоэффициент размера шага адаптации, заданный как скалярное, неотрицательное числовое значение. Для сходимости нормализованного метода LMS, размер шага должен быть больше 0 и меньше 2. Тип данных входного параметра размера шага должен совпадать с типом данных x и d. Если тип данных является фиксированной точкой, тип данных должен быть подписан.
Размер небольшого шага обеспечивает небольшую установившуюся ошибку между выходом y и желаемый сигнал d. Если размер шага невелик, скорость сходимости фильтра уменьшается. Чтобы улучшить скорость сходимости, увеличьте размер шага. Обратите внимание, что если размер шага велик, фильтр может стать нестабильным. Чтобы вычислить максимальный размер шага, который фильтр может принять, не становясь нестабильным, используйте maxstep функция.
Этот вход требуется, когда для свойства StepSizeSource задано значение 'Input port'.
Типы данных: single | double | int8 | int16 | int32 | int64 | fi
a - Управление адаптациейВход управления адаптацией, который управляет обновлением весов фильтра. Если значение этого входа ненулевое, объект постоянно обновляет веса фильтров. Если значение этого входа меньше нуля, веса фильтров остаются на своем текущем значении.
Этот вход требуется, когда для свойства AdaptInportPort задано значение true.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
r - Сигнал сбросаСигнал сброса, который сбрасывает веса фильтра на основе значений свойства WeightsResetCondition.
Этот вход требуется, когда для свойства WeightsResetInportPort задано значение true.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
y - Отфильтрованный выходФильтрация выхода, возврат в виде скаляра или вектора-столбца. Объект адаптирует свои веса фильтра, чтобы сходиться входной сигнал x чтобы соответствовать требуемому сигналу d. Фильтр выводит сходимый сигнал.
Типы данных: single | double | int8 | int16 | int32 | int64 | fi
Поддержка комплексного числа: Да
err - Различие между выходным и желаемым сигналомРазличие между сигналом выхода y и желаемый сигнал d, возвращается в виде скаляра или вектора-столбца. Тип данных err соответствует типу данных y. Цель адаптивного фильтра состоит в том, чтобы минимизировать эту ошибку. Объект адаптирует свои веса, чтобы сходиться к оптимальным весам фильтра, которые формируют сигнал выхода, который тесно совпадает с желаемым сигналом. Для получения дополнительной информации о том, как err вычисляется, см. Алгоритмы.
Типы данных: single | double | int8 | int16 | int32 | int64 | fi
wts - Веса адаптивных фильтровВеса адаптивного фильтра, возвращенные в виде скаляра или вектора-столбца длины, заданной значением в Length.
Типы данных: single | double | int8 | int16 | int32 | int64 | fi
Чтобы использовать функцию объекта, задайте системный объект в качестве первого входного параметра. Например, чтобы освободить системные ресурсы системного объекта с именем obj, используйте следующий синтаксис:
release(obj)
Средняя квадратичная невязка (MSE) измеряет среднее значение квадратов ошибок между желаемым сигналом и входом первичного сигнала к адаптивному фильтру. Уменьшение этой ошибки сходит первичный входной параметр к желаемому сигналу. Определите предсказанное значение MSE и моделируемое значение MSE в каждый момент времени, используя msepred и msesim функций. Сравните эти значения MSE друг с другом и относительно минимальных значений MSE и установившегося MSE. В сложение вычислите сумму квадратов ошибок коэффициента, заданных трассировкой коэффициента ковариации матрице.
Примечание.Если вы используете R2016a или более ранний релиз, замените каждый вызов объекта эквивалентным синтаксисом шага. Для примера, obj(x) становится step(obj,x).
Инициализация
Создайте dsp.FIRFilter Системный object™, который представляет неизвестную систему. Передайте сигнал, x, к конечная импульсная характеристика. Выходы неизвестной системы являются желаемым сигналом, d, которая является суммой выходов неизвестной системы (конечная импульсная характеристика) и аддитивного сигнала шума, n.
num = fir1(31,0.5); fir = dsp.FIRFilter('Numerator',num); iir = dsp.IIRFilter('Numerator',sqrt(0.75),... 'Denominator',[1 -0.5]); x = iir(sign(randn(2000,25))); n = 0.1*randn(size(x)); d = fir(x) + n;
Фильтр LMS
Создайте dsp.LMSFilter Системный объект для создания фильтра, который адаптируется для вывода необходимого сигнала. Установите длину адаптивного фильтра равную 32 отводам, размер шага равным 0,008, и коэффициент десятикратного уменьшения для анализа и симуляции равным 5. Переменная simmse представляет моделируемый MSE между выходами неизвестной системы, d, и выходы адаптивного фильтра. Переменная mse задает соответствующее предсказанное значение.
l = 32; mu = 0.008; m = 5; lms = dsp.LMSFilter('Length',l,'StepSize',mu); [mmse,emse,meanW,mse,traceK] = msepred(lms,x,d,m); [simmse,meanWsim,Wsim,traceKsim] = msesim(lms,x,d,m);
Постройте график результатов MSE
Сравните значения моделируемого MSE, предсказанного MSE, минимального MSE и окончательного MSE. Окончательное значение MSE определяется суммой минимального MSE и избытка MSE.
nn = m:m:size(x,1); semilogy(nn,simmse,[0 size(x,1)],[(emse+mmse)... (emse+mmse)],nn,mse,[0 size(x,1)],[mmse mmse]) title('Mean Squared Error Performance') axis([0 size(x,1) 0.001 10]) legend('MSE (Sim.)','Final MSE','MSE','Min. MSE') xlabel('Time Index') ylabel('Squared Error Value')

Предсказанный MSE следует той же траектории, что и моделируемый MSE. Обе эти траектории сходятся с установившейся (конечной) MSE.
Постройте график траекторий коэффициентов
meanWsim - среднее значение моделируемых коэффициентов, заданное как msesim. meanW - среднее значение предсказанных коэффициентов, заданное как msepred.
Сравните моделируемые и предсказанные средние значения коэффициентов 12,13,14 и 15 фильтра LMS.
plot(nn,meanWsim(:,12),'b',nn,meanW(:,12),'r',nn,... meanWsim(:,13:15),'b',nn,meanW(:,13:15),'r') PlotTitle ={'Average Coefficient Trajectories for';... 'W(12), W(13), W(14), and W(15)'}
PlotTitle = 2x1 cell
{'Average Coefficient Trajectories for'}
{'W(12), W(13), W(14), and W(15)' }
title(PlotTitle) legend('Simulation','Theory') xlabel('Time Index') ylabel('Coefficient Value')

В установившемся состоянии обе траектории сходятся.
Сумма квадратов ошибок коэффициента
Сравните сумму квадратов ошибок коэффициента, заданную как msepred и msesim. Эти значения заданы трассировкой ковариационной матрицы коэффициента.
semilogy(nn,traceKsim,nn,traceK,'r') title('Sum-of-Squared Coefficient Errors') axis([0 size(x,1) 0.0001 1]) legend('Simulation','Theory') xlabel('Time Index') ylabel('Squared Error Value')

The maxstep функция вычисляет максимальный размер шага адаптивного фильтра. Этот размер шага сохраняет фильтр стабильным на максимально возможной скорости сходимости. Создайте основной входной сигнал, x, путем передачи подписанного случайного сигнала в БИХ. Сигнальное x содержит 50 системы координат по 2000 выборок каждой системы координат. Создайте фильтр LMS с 32 отводами и размером шага 0,1.
x = zeros(2000,50); IIRFilter = dsp.IIRFilter('Numerator',sqrt(0.75),'Denominator',[1 -0.5]); for k = 1:size(x,2) x(:,k) = IIRFilter(sign(randn(size(x,1),1))); end mu = 0.1; LMSFilter = dsp.LMSFilter('Length',32,'StepSize',mu);
Вычислите максимальный размер шага адаптации и максимальный размер шага в среднеквадратичном смысле с помощью maxstep функция.
[mumax,mumaxmse] = maxstep(LMSFilter,x)
mumax = 0.0625
mumaxmse = 0.0536
Система идентификации является процессом идентификации коэффициентов неизвестной системы с помощью адаптивного фильтра. Общий обзор процесса показан на Систему идентификации - Использование адаптивного фильтра для идентификации неизвестной системы. Основными компонентами являются:
Алгоритм адаптивного фильтра. В этом примере установите Method свойство dsp.LMSFilter на 'LMS' для выбора алгоритма адаптивного фильтра LMS.
Неизвестная система или процесс для адаптации. В этом примере фильтр разработан fircband - неизвестная система.
Соответствующие входные данные для осуществления процесса адаптации. Для типовой модели LMS это желаемый сигнал и входной сигнал .
Цель адаптивного фильтра состоит в том, чтобы минимизировать сигнал ошибки между выходом адаптивного фильтра и выходы неизвестной системы (или системы, которая будет идентифицирована) . Когда сигнал ошибки минимизируется, адаптированный фильтр напоминает неизвестную систему. Коэффициенты обоих фильтров тесно совпадают.
Примечание.Если вы используете R2016a или более ранний релиз, замените каждый вызов объекта эквивалентным синтаксисом шага. Для примера, obj(x) становится step(obj,x).
Неизвестная система
Создайте dsp.FIRFilter объект, который представляет систему, которая будет идентифицирована. Используйте fircband функция для разработки коэффициентов фильтра. Спроектированный фильтр является lowpass фильтром, ограниченным 0,2 пульсации в полосе остановки.
filt = dsp.FIRFilter; filt.Numerator = fircband(12,[0 0.4 0.5 1],[1 1 0 0],[1 0.2],... {'w' 'c'});
Передайте сигнал x к конечная импульсная характеристика. Требуемый сигнал d - сумма выхода неизвестной системы ( конечная импульсная характеристика) и аддитивного сигнала шума n.
x = 0.1*randn(250,1); n = 0.01*randn(250,1); d = filt(x) + n;
Адаптивный фильтр
При помощи неизвестного фильтра и требуемого сигнала на месте создайте и примените адаптивный объект фильтра LMS для идентификации неизвестного фильтра.
Подготовка объекта адаптивного фильтра требует начальных значений для оценок коэффициентов фильтра и размера шага LMS (mu). Можно начать с некоторого набора ненулевых значений как оценок для коэффициентов фильтра. Этот пример использует нули для 13 начальных весов фильтра. Установите InitialConditions свойство dsp.LMSFilter к желаемым начальным значениям весов фильтра. Для размера шага 0,8 является хорошим компромиссом между достаточно большим, чтобы хорошо сходиться в пределах 250 итераций (250 входных точек выборки) и достаточно маленьким, чтобы создать точную оценку неизвестного фильтра.
Создайте dsp.LMSFilter объект для представления адаптивного фильтра, который использует адаптивный алгоритм LMS. Установите длину адаптивного фильтра равную 13 отводам, а размер шага равным 0,8.
mu = 0.8;
lms = dsp.LMSFilter(13,'StepSize',mu)lms =
dsp.LMSFilter with properties:
Method: 'LMS'
Length: 13
StepSizeSource: 'Property'
StepSize: 0.8000
LeakageFactor: 1
InitialConditions: 0
AdaptInputPort: false
WeightsResetInputPort: false
WeightsOutput: 'Last'
Show all properties
Передайте основной входной сигнал x и желаемый сигнал d в фильтр LMS. Запустите адаптивный фильтр, чтобы определить неизвестную систему. Область выхода y адаптивного фильтра является сигнал, сходящийся к желаемому сигналу d, таким образом минимизируя ошибку e между двумя сигналами.
Постройте график результатов. Сигнал выхода не совпадает с желаемым сигналом, как ожидалось, делая ошибку между двумя нетривиальными.
[y,e,w] = lms(x,d); plot(1:250, [d,y,e]) title('System Identification of an FIR filter') legend('Desired','Output','Error') xlabel('Time index') ylabel('Signal value')

Сравнение весов
Вектор весов w представляет коэффициенты фильтра LMS, который выполнен с возможностью напоминания неизвестной системы ( конечная импульсная характеристика). Чтобы подтвердить сходимость, сравните числитель конечной импульсной характеристики и оценочные веса адаптивного фильтра.
Оцененные веса фильтра не совпадают с фактическими весами фильтра, подтверждая результаты, показанные на предыдущем графике сигнала.
stem([(filt.Numerator).' w]) title('System Identification by Adaptive LMS Algorithm') legend('Actual filter weights','Estimated filter weights',... 'Location','NorthEast')

Изменение размера шага
В качестве эксперимента измените размер шага на 0,2. Повторение примера с mu = 0.2 Результаты следующими диаграммами лист-ствол. Фильтры не сходятся, и предполагаемые веса не являются хорошими приближениями фактических весов.
mu = 0.2; lms = dsp.LMSFilter(13,'StepSize',mu); [~,~,w] = lms(x,d); stem([(filt.Numerator).' w]) title('System Identification by Adaptive LMS Algorithm') legend('Actual filter weights','Estimated filter weights',... 'Location','NorthEast')

Увеличение количества выборок данных
Увеличьте формат кадра необходимого сигнала. Несмотря на то, что это увеличивает расчет участия, LMS-алгоритм теперь имеет больше данных, которые могут использоваться для адаптации. При 1000 выборках данных сигнала и размере шага 0,2 коэффициенты выравниваются ближе, чем раньше, что указывает на улучшенную сходимость.
release(filt); x = 0.1*randn(1000,1); n = 0.01*randn(1000,1); d = filt(x) + n; [y,e,w] = lms(x,d); stem([(filt.Numerator).' w]) title('System Identification by Adaptive LMS Algorithm') legend('Actual filter weights','Estimated filter weights',... 'Location','NorthEast')

Увеличьте количество выборок данных дополнительно путем ввода данных через итерации. Запустите алгоритм на 4000 выборках данных, переданных в LMS-алгоритм пакетами 1000 выборки в 4 итерациях.
Сравните веса фильтров. Веса LMS-фильтра очень близко совпадают с весами конечной импульсной характеристики, что указывает на хорошую сходимость.
release(filt); n = 0.01*randn(1000,1); for index = 1:4 x = 0.1*randn(1000,1); d = filt(x) + n; [y,e,w] = lms(x,d); end stem([(filt.Numerator).' w]) title('System Identification by Adaptive LMS Algorithm') legend('Actual filter weights','Estimated filter weights',... 'Location','NorthEast')

Сигнал выхода очень близко соответствует желаемому сигналу, делая ошибку между ними близкой к нулю.
plot(1:1000, [d,y,e]) title('System Identification of an FIR filter') legend('Desired','Output','Error') xlabel('Time index') ylabel('Signal value')

Чтобы улучшить эффективность LMS-алгоритма, нормализованный вариант (NLMS) использует адаптивный размер шага, основанный на степени сигнала. Когда изменяется степень входного сигнала, алгоритм вычисляет вход степени и настраивает размер шага, чтобы сохранить соответствующее значение. Размер шага изменяется со временем, и в результате нормализованный алгоритм быстрее сходится с меньшим количеством выборок во многих случаях. Для входных сигналов, которые изменяются медленно с течением времени, нормализованный LMS-алгоритм может быть более эффективным подходом LMS.
Для получения примера, использующей подход LMS, смотрите Систему идентификации конечной импульсной характеристики Filter Using LMS-алгоритма.
Примечание.Если вы используете R2016a или более ранний релиз, замените каждый вызов объекта эквивалентным синтаксисом шага. Для примера, obj(x) становится step(obj,x).
Неизвестная система
Создайте dsp.FIRFilter объект, который представляет систему, которая будет идентифицирована. Используйте fircband функция для разработки коэффициентов фильтра. Спроектированный фильтр является lowpass фильтром, ограниченным 0,2 пульсации в полосе остановки.
filt = dsp.FIRFilter; filt.Numerator = fircband(12,[0 0.4 0.5 1],[1 1 0 0],[1 0.2],... {'w' 'c'});
Передайте сигнал x к конечная импульсная характеристика. Требуемый сигнал d - сумма выхода неизвестной системы ( конечная импульсная характеристика) и аддитивного сигнала шума n.
x = 0.1*randn(1000,1); n = 0.001*randn(1000,1); d = filt(x) + n;
Адаптивный фильтр
Чтобы использовать нормированное изменение LMS-алгоритма, установите Method свойство на dsp.LMSFilter на 'Normalized LMS'. Установите длину адаптивного фильтра равную 13 отводам, а размер шага равным 0,2.
mu = 0.2; lms = dsp.LMSFilter(13,'StepSize',mu,'Method',... 'Normalized LMS');
Передайте основной входной сигнал x и желаемый сигнал d в фильтр LMS.
[y,e,w] = lms(x,d);
Область выхода y адаптивного фильтра является сигнал, сходящийся к желаемому сигналу d, таким образом минимизируя ошибку e между двумя сигналами.
plot(1:1000, [d,y,e]) title('System Identification by Normalized LMS Algorithm') legend('Desired','Output','Error') xlabel('Time index') ylabel('Signal value')

Сравнение адаптированного фильтра с неизвестной системой
Вектор w весов представляет коэффициенты LMS-фильтра, который приспособлен напоминать неизвестную систему ( конечную импульсную характеристику). Чтобы подтвердить сходимость, сравните числитель конечной импульсной характеристики и оценочные веса адаптивного фильтра.
stem([(filt.Numerator).' w]) title('System Identification by Normalized LMS Algorithm') legend('Actual filter weights','Estimated filter weights',... 'Location','NorthEast')

Адаптивный фильтр адаптирует свои коэффициенты фильтра так, чтобы они совпадали с коэффициентами неизвестной системы. Цель состоит в том, чтобы минимизировать сигнал ошибки между выходом неизвестной системы и выходом адаптивного фильтра. Когда эти два выхода сходятся и тесно совпадают для одного и того же входа, говорят, что коэффициенты тесно совпадают. Адаптивный фильтр в этом состоянии напоминает неизвестную систему. Этот пример сравнивает скорость, с которой это сходимость происходит для нормализованного алгоритма LMS (NLMS) и LMS-алгоритма без нормализации.
Неизвестная система
Создайте dsp.FIRFilter который представляет неизвестную систему. Передайте сигнал x как вход в неизвестную систему. Требуемый сигнал d - сумма выхода неизвестной системы ( конечная импульсная характеристика) и аддитивного сигнала шума n.
filt = dsp.FIRFilter; filt.Numerator = fircband(12,[0 0.4 0.5 1],[1 1 0 0],[1 0.2],... {'w' 'c'}); x = 0.1*randn(1000,1); n = 0.001*randn(1000,1); d = filt(x) + n;
Адаптивный фильтр
Создайте два dsp.LMSFilter объекты с одним набором в LMS-алгоритм, а другой - в нормализованный LMS-алгоритм. Выберите размер шага адаптации 0,2 и установите длину адаптивного фильтра равной 13 отводам.
mu = 0.2; lms_nonnormalized = dsp.LMSFilter(13,'StepSize',mu,... 'Method','LMS'); lms_normalized = dsp.LMSFilter(13,'StepSize',mu,... 'Method','Normalized LMS');
Передайте основной входной сигнал x и желаемый сигнал d к обоим изменениям LMS-алгоритма. Переменные e1 и e2 представляют ошибку между желаемым сигналом и выходом нормализованных и неормализированных фильтров, соответственно.
[~,e1,~] = lms_normalized(x,d); [~,e2,~] = lms_nonnormalized(x,d);
Постройте график сигналов ошибки для обоих изменений. Сигнал ошибки для варианта NLMS сходится к нулю намного быстрее, чем сигнал ошибки для варианта LMS. Нормированная версия адаптируется в гораздо меньшем количестве итераций к результату почти так же хорошо, как и неормализированная версия.
plot([e1,e2]); title('Comparing the LMS and NLMS Conversion Performance'); legend('NLMS derived filter weights', ... 'LMS derived filter weights','Location', 'NorthEast'); xlabel('Time index') ylabel('Signal value')

Отмените аддитивный шум n, добавленный в неизвестную систему с помощью адаптивного фильтра LMS. Фильтр LMS адаптирует свои коэффициенты до тех пор, пока его передаточная функция не будет максимально точно соответствовать передаточной функции неизвестной системы. Различие между выходом адаптивного фильтра и выхода неизвестной системы представляет сигнал ошибки e. Минимизация этого сигнала ошибки является целью адаптивного фильтра.
Неизвестная система и фильтр LMS обрабатывают один и тот же входной сигнал, x, и производить выходы d и y, соответственно. Если коэффициенты адаптивного фильтра совпадают с коэффициентами неизвестной системы, ошибка, e, в эффект представляет собой аддитивный шум.
Примечание.Если вы используете R2016a или более ранний релиз, замените каждый вызов объекта эквивалентным синтаксисом шага. Для примера, obj(x) становится step(obj,x).
Создайте dsp.FIRFilter Системный объект, представляющий неизвестную систему. Создайте dsp.LMSFilter Объекту и установите длину равную 11 отводам, а размер шага равным 0,05. Создайте синусоиду, чтобы представлять шум, добавленный в неизвестную систему. Просмотрите сигналы в временных возможностях.
FrameSize = 100; NIter = 10; lmsfilt2 = dsp.LMSFilter('Length',11,'Method','Normalized LMS', ... 'StepSize',0.05); firfilt2 = dsp.FIRFilter('Numerator', fir1(10,[.5, .75])); sinewave = dsp.SineWave('Frequency',0.01, ... 'SampleRate',1,'SamplesPerFrame',FrameSize); scope = timescope('TimeUnits','Seconds',... 'YLimits',[-3 3],'BufferLength',2*FrameSize*NIter, ... 'ShowLegend',true,'ChannelNames', ... {'Noisy signal', 'Error signal'});
Создайте случайный входной сигнал x и передайте сигнал в конечную импульсную характеристику фильтр. Добавьте синусоиду к выходу конечной импульсной характеристики, чтобы сгенерировать сигнал с шумом, d. Сигнал, d является выходом неизвестной системы. Передайте сигнал с шумом и основной входной сигнал в фильтр LMS. Просмотрите сигнал с шумом и сигнал ошибки во временных возможностях.
for k = 1:NIter x = randn(FrameSize,1); d = firfilt2(x) + sinewave(); [y,e,w] = lmsfilt2(x,d); scope([d,e]) end release(scope)

Сигнал ошибки, e, - синусоидальный шум, добавленный к неизвестной системе. Минимизация сигнала ошибки минимизирует шум, добавляемый в систему.
Когда количество расчета, требуемое для вывода адаптивного фильтра, управляет вашим процессом разработки, вариант sign-data алгоритма LMS (SDLMS) может быть очень хорошим выбором, как показано в этом примере.
В стандартных и нормированных изменениях адаптивного фильтра LMS коэффициенты для адаптирующего фильтра возникают из-за средней квадратной ошибки между желаемым сигналом и выходом сигналом от неизвестной системы. Алгоритм sign-data изменяет среднее вычисление квадратной ошибки с помощью знака входных данных, чтобы изменить коэффициенты фильтра.
Когда ошибка положительная, новые коэффициенты являются предыдущими коэффициентами плюс ошибка, умноженная на размер шага Если ошибка отрицательная, новые коэффициенты снова являются предыдущими коэффициентами минус ошибка, умноженная на, - обратите внимание на изменение знака.
Когда вход равен нулю, новые коэффициенты те же, что и в предыдущем наборе.
В векторной форме LMS-алгоритм со знаком-данными является:
где
с вектором содержащие веса, примененные к коэффициентам фильтра и вектору содержит входные данные. Вектор - ошибка между желаемым сигналом и отфильтрованным сигналом. Цель алгоритма SDLMS состоит в том, чтобы минимизировать эту ошибку. Размер шага представлен .
С меньшим коррекция к весам фильтра становится меньше для каждой выборки, и ошибка SDLMS падает медленнее. Большее изменяет веса больше для каждого шага, поэтому ошибка падает быстрее, но полученная ошибка не приближается к идеальному решению так близко. Чтобы гарантировать хорошую скорость сходимости и стабильность, выберите в пределах следующих практических границ.
где - количество выборок в сигнале. Кроме того, задайте как степень двойки для эффективных вычислений.
Примечание: То, как вы устанавливаете начальные условия алгоритма sign-data, глубоко влияет на эффективность процесса адаптации. Поскольку алгоритм по существу квантует входной сигнал, алгоритм может легко стать нестабильным.
Серия больших входных значений в сочетании с процессом квантования может привести к росту ошибки за все границы. Ограничьте склонность алгоритма sign-data к выходу из-под контроля, выбрав небольшой размер шага и установка начальных условий для алгоритма ненулевых положительных и отрицательных значений.
В этом примере шумоподавления установите Method свойство dsp.LMSFilter на 'Sign-Data LMS'. Этот пример требует двух наборов входных данных:
Данные, содержащие сигнал, поврежденный шумом. На блоке под шумом или подавлением помех - Использование адаптивного фильтра для удаления шума из неизвестной системы, это желаемый сигнал . Процесс шумоподавления удаляет шум из сигнала.
Данные, содержащие случайный шум. На блоке под шумом или подавлением помех - Использование адаптивного фильтра для удаления шума из неизвестной системы, это . Сигнал коррелирует с шумом, который повреждает данные сигнала. Без корреляции между данными о шуме алгоритм адаптации не может удалить шум из сигнала.
Для сигнала используйте синусоиду. Обратите внимание, что signal - вектор-столбец из 1000 элементов.
signal = sin(2*pi*0.055*(0:1000-1)');
Теперь добавьте коррелированный белый шум к signal. Чтобы убедиться, что шум коррелирует, передайте шум через lowpass конечная импульсная характеристика и затем добавьте отфильтрованный шум к сигналу.
noise = randn(1000,1); filt = dsp.FIRFilter; filt.Numerator = fir1(11,0.4); fnoise = filt(noise); d = signal + fnoise;
fnoise - коррелированный шум и d теперь является желаемым входом в алгоритм sign-data.
Подготовка dsp.LMSFilter объект для обработки, установите начальные условия весов и mu фильтра (StepSize). Как отмечалось ранее в этом разделе, значения, которые вы задаете для coeffs и mu определите, может ли адаптивный фильтр удалить шум из пути сигнала.
В Система Идентификации of FIR Filter Using LMS Algorithm вы создали фильтр по умолчанию, который устанавливает коэффициенты фильтра в нули. В большинстве случаев этот подход не работает для алгоритма sign-data. Чем ближе вы устанавливаете свои начальные коэффициенты фильтра к ожидаемым значениям, тем больше вероятность, что алгоритм остается хорошо поведенным и сходится к решению фильтра, которое эффективно удаляет шум.
В данном примере начнем с коэффициентов, используемых в шумовом фильтре (filt.Numerator), и немного измените их, чтобы алгоритм должен адаптироваться.
coeffs = (filt.Numerator).'-0.01; % Set the filter initial conditions. mu = 0.05; % Set the step size for algorithm updating.
С необходимыми входными параметрами для dsp.LMSFilter подготовленный, создайте объект фильтра LMS, запустите адаптацию и просмотрите результаты.
lms = dsp.LMSFilter(12,'Method','Sign-Data LMS',... 'StepSize',mu,'InitialConditions',coeffs); [~,e] = lms(noise,d); L = 200; plot(0:L-1,signal(1:L),0:L-1,e(1:L)); title('Noise Cancellation by the Sign-Data Algorithm'); legend('Actual signal','Result of noise cancellation',... 'Location','NorthEast'); xlabel('Time index') ylabel('Signal values')

Когда dsp.LMSFilter запускается, он использует гораздо меньше операций умножения, чем любой из стандартных LMS-алгоритмов. Кроме того, выполнение адаптации данных о знаках требует только умножения на перемену бит, когда размер шага является степенью двойки.
Несмотря на то, эффективность алгоритма sign-data, как показано на этом графике, довольно хороша, алгоритм sign-data намного менее стабилен, чем стандартные изменения LMS. В этом примере шумоподавления обработанный сигнал является очень хорошим соответствием входному сигналу, но алгоритм может очень легко расти без привязки, а не достигать хорошей эффективности.
Изменение начальных условий веса (InitialConditions) и mu (StepSize), или даже фильтр lowpass, который вы использовали для создания коррелированного шума, может вызвать отказ шумоподавления.
В стандартных и нормированных изменениях адаптивного фильтра LMS коэффициенты для адаптирующего фильтра возникают из вычисления средней квадратной ошибки между желаемым сигналом и выходом сигналом от неизвестной системы и применения результата к текущим коэффициентам фильтра. Алгоритм LMS (SELMS) заменяет вычисление средней квадратной ошибки, используя знак ошибки, чтобы изменить коэффициенты фильтра.
Когда ошибка положительная, новые коэффициенты являются предыдущими коэффициентами плюс ошибка, умноженная на размер шага . Если ошибка отрицательная, новые коэффициенты являются предыдущими коэффициентами минус ошибка, умноженная на - обратите внимание на изменение знака. Когда вход равен нулю, новые коэффициенты те же, что и в предыдущем наборе.
В векторной форме LMS-алгоритм является:
,
где
с вектором содержащие веса, примененные к коэффициентам фильтра и вектору содержит входные данные. Вектор - ошибка между желаемым сигналом и отфильтрованным сигналом. Цель алгоритма SELMS состоит в том, чтобы минимизировать эту ошибку.
С меньшим коррекция к весам фильтра становится меньше для каждой выборки, и ошибка SELMS падает более медленно. Большее изменяет веса больше для каждого шага, поэтому ошибка падает быстрее, но полученная ошибка не приближается к идеальному решению так близко. Чтобы гарантировать хорошую скорость сходимости и стабильность, выберите в пределах следующих практических границ.
где - количество выборок в сигнале. Кроме того, задайте как степень двойки для эффективного расчета.
Примечание: То, как вы устанавливаете начальные условия алгоритма ошибки знака, глубоко влияет на эффективность процесса адаптации. Поскольку алгоритм по существу квантует сигнал ошибки, алгоритм может легко стать нестабильным.
Серия больших значений ошибки в сочетании с процессом квантования может привести к росту ошибки за все границы. Ограничьте склонность алгоритма sign-error стать нестабильным, выбрав небольшой размер шага и установка начальных условий для алгоритма ненулевых положительных и отрицательных значений.
В этом примере шумоподавления установите Method свойство dsp.LMSFilter на 'Sign-Error LMS'. Этот пример требует двух наборов входных данных:
Данные, содержащие сигнал, поврежденный шумом. На блоке под шумом или подавлением помех - Использование адаптивного фильтра для удаления шума из неизвестной системы, это желаемый сигнал . Процесс шумоподавления удаляет шум из сигнала.
Данные, содержащие случайный шум. На блоке под шумом или подавлением помех - Использование адаптивного фильтра для удаления шума из неизвестной системы, это . Сигнал коррелирует с шумом, который повреждает данные сигнала. Без корреляции между данными о шуме алгоритм адаптации не может удалить шум из сигнала.
Для сигнала используйте синусоиду. Обратите внимание, что signal - вектор-столбец из 1000 элементов.
signal = sin(2*pi*0.055*(0:1000-1)');
Теперь добавьте коррелированный белый шум к signal. Чтобы убедиться, что шум коррелирует, передайте шум через lowpass конечная импульсная характеристика и затем добавьте отфильтрованный шум к сигналу.
noise = randn(1000,1); filt = dsp.FIRFilter; filt.Numerator = fir1(11,0.4); fnoise = filt(noise); d = signal + fnoise;
fnoise - коррелированный шум и d теперь является желаемым входом в алгоритм sign-error.
Подготовка dsp.LMSFilter объект для обработки, установите начальные условия весов фильтра (InitialConditions) и mu (StepSize). Как отмечалось ранее в этом разделе, значения, которые вы задаете для coeffs и mu определите, может ли адаптивный фильтр удалить шум из пути сигнала.
В Система Идентификации of FIR Filter Using LMS Algorithm вы создали фильтр по умолчанию, который устанавливает коэффициенты фильтра в нули. В большинстве случаев этот подход не работает для алгоритма ошибки знака. Чем ближе вы устанавливаете свои начальные коэффициенты фильтра к ожидаемым значениям, тем больше вероятность, что алгоритм остается хорошо поведенным и сходится к решению фильтра, которое эффективно удаляет шум.
В данном примере начнем с коэффициентов, используемых в шумовом фильтре (filt.Numerator) и слегка измените их, чтобы алгоритм должен адаптироваться.
coeffs = (filt.Numerator).'-0.01; % Set the filter initial conditions. mu = 0.05; % Set the step size for algorithm updating.
С необходимыми входными параметрами для dsp.LMSFilter подготовлен, запустите адаптацию и посмотрите результаты.
lms = dsp.LMSFilter(12,'Method','Sign-Error LMS',... 'StepSize',mu,'InitialConditions',coeffs); [~,e] = lms(noise,d); L = 200; plot(0:199,signal(1:200),0:199,e(1:200)); title('Noise cancellation performance by the sign-error LMS algorithm'); legend('Actual signal','Error after noise reduction',... 'Location','NorthEast') xlabel('Time index') ylabel('Signal value')

Когда запускается алгоритм LMS со знаком-ошибкой, он использует гораздо меньше операций умножения, чем любой из стандартных LMS-алгоритмов. Кроме того, выполнение адаптации ошибки знака требует только множителей перемены бит, когда размер шага является степенью двойки.
Несмотря на то, что эффективность алгоритма sign-error, как показано на этом графике, довольно хороша, алгоритм sign-error намного менее стабилен, чем стандартные изменения LMS. В этом примере шумоподавления адаптированный сигнал является очень хорошим соответствием входному сигналу, но алгоритм может очень легко стать нестабильным, а не достигать хорошей эффективности.
Изменение начальных условий веса (InitialConditions) и mu (StepSize), или даже lowpass, который вы использовали для создания коррелированного шума, может вызвать отказ шумоподавления, и алгоритм станет бесполезным.
LMS-алгоритм со знаком (SSLMS) заменяет вычисление средней квадратной ошибки, используя знак входных данных, чтобы изменить коэффициенты фильтра. Когда ошибка положительная, новые коэффициенты являются предыдущими коэффициентами плюс ошибка, умноженная на размер шага . Если ошибка отрицательная, новые коэффициенты являются предыдущими коэффициентами минус ошибка, умноженная на - обратите внимание на изменение знака. Когда вход равен нулю, новые коэффициенты те же, что и в предыдущем наборе.
В сущности, алгоритм квантует и ошибку, и вход, применяя к ним оператор знака.
В векторной форме LMS-алгоритм является:
где
Вектор содержит веса, примененные к коэффициентам фильтра, и вектор содержит входные данные. Вектор - ошибка между желаемым сигналом и отфильтрованным сигналом. Цель алгоритма SSLMS состоит в том, чтобы минимизировать эту ошибку.
С меньшим коррекция к весам фильтра становится меньше для каждой выборки, и ошибка SSLMS падает более медленно. Большее изменяет веса больше для каждого шага, поэтому ошибка падает быстрее, но полученная ошибка не приближается к идеальному решению так близко. Чтобы гарантировать хорошую скорость сходимости и стабильность, выберите в пределах следующих практических границ.
где - количество выборок в сигнале. Кроме того, задайте как степень двойки для эффективных расчетов
Примечание:
То, как вы устанавливаете начальные условия алгоритма знака, глубоко влияет на эффективность процесса адаптации. Поскольку алгоритм по существу квантует входной сигнал и сигнал ошибки, алгоритм может легко стать нестабильным.
Серия больших значений ошибки в сочетании с процессом квантования может привести к росту ошибки за все границы. Сдерживайте склонность алгоритма знака-знака стать нестабильным, выбирая небольшой размер шага и установка начальных условий для алгоритма ненулевых положительных и отрицательных значений.
В этом примере шумоподавления установите Method свойство dsp.LMSFilter на 'Sign-Sign LMS'. Этот пример требует двух наборов входных данных:
Данные, содержащие сигнал, поврежденный шумом. На блоке под шумом или подавлением помех - Использование адаптивного фильтра для удаления шума из неизвестной системы, это желаемый сигнал . Процесс шумоподавления удаляет шум из сигнала.
Данные, содержащие случайный шум. На блоке под шумом или подавлением помех - Использование адаптивного фильтра для удаления шума из неизвестной системы, это . Сигнал коррелирует с шумом, который повреждает данные сигнала. Без корреляции между данными о шуме алгоритм адаптации не может удалить шум из сигнала.
Для сигнала используйте синусоиду. Обратите внимание, что signal - вектор-столбец из 1000 элементов.
signal = sin(2*pi*0.055*(0:1000-1)');
Теперь добавьте коррелированный белый шум к signal. Чтобы убедиться, что шум коррелирует, передайте шум через lowpass конечная импульсная характеристика, затем добавьте отфильтрованный шум к сигналу.
noise = randn(1000,1); filt = dsp.FIRFilter; filt.Numerator = fir1(11,0.4); fnoise = filt(noise); d = signal + fnoise;
fnoise - коррелированный шум и d теперь является желаемым входом в алгоритм знака.
Подготовка dsp.LMSFilter объект для обработки, установите начальные условия весов фильтра (InitialConditions) и mu (StepSize). Как отмечалось ранее в этом разделе, значения, которые вы задаете для coeffs и mu определите, может ли адаптивный фильтр удалить шум из пути сигнала. В Система Идентификации of FIR Filter Using LMS Algorithm вы создали фильтр по умолчанию, который устанавливает коэффициенты фильтра в нули. Обычно этот подход не работает для алгоритма знака-знака.
Чем ближе вы устанавливаете свои начальные коэффициенты фильтра к ожидаемым значениям, тем больше вероятность, что алгоритм остается хорошо поведенным и сходится к решению фильтра, которое эффективно удаляет шум. В данном примере вы начинаете с коэффициентов, используемых в шумовом фильтре (filt.Numerator), и немного измените их, чтобы алгоритм должен адаптироваться.
coeffs = (filt.Numerator).' -0.01; % Set the filter initial conditions.
mu = 0.05;С необходимыми входными параметрами для dsp.LMSFilter подготовлен, запустите адаптацию и посмотрите результаты.
lms = dsp.LMSFilter(12,'Method','Sign-Sign LMS',... 'StepSize',mu,'InitialConditions',coeffs); [~,e] = lms(noise,d); L = 200; plot(0:199,signal(1:200),0:199,e(1:200)); title('Noise cancellation performance by the sign-sign LMS algorithm'); legend('Actual signal','Error after noise reduction',... 'Location','NorthEast') xlabel('Time index') ylabel('Signal value')

Когда dsp.LMSFilter запускается, он использует гораздо меньше операций умножения, чем любой из стандартных LMS-алгоритмов. Кроме того, выполнение адаптации знака-знака требует только множителей перемены бит, когда размер шага является степенью двойки.
Несмотря на то, что эффективность алгоритма знака-знака, как показано на этом графике, довольно хороша, алгоритм знака-знака намного менее стабилен, чем стандартные изменения LMS. В этом примере шумоподавления адаптированный сигнал является очень хорошим соответствием входному сигналу, но алгоритм может очень легко стать нестабильным, а не достигать хорошей эффективности.
Изменение начальных условий веса (InitialConditions) и mu (StepSize), или даже lowpass, который вы использовали для создания коррелированного шума, может вызвать отказ шумоподавления, и алгоритм станет бесполезным.
Примечание.Этот пример выполняется только в R2017a или более поздней версии. Если вы используете релиз раньше R2017a, объект не выводит полную историю весов фильтра по образцам. Если вы используете релиз раньше R2016b, замените каждый вызов функции на эквивалентный step синтаксис. Для примера, myObject(x) становится step(myObject,x).
Инициализируйте dsp.LMSFilter Системный объект и установите WeightsOutput свойство к 'All'. Эта настройка позволяет фильтру LMS выводить матрицу весов с размерностями [FrameLength Length], соответствующий полной истории дискретизации весов для всех FrameLength выборки значений входа.
FrameSize = 15000; lmsfilt3 = dsp.LMSFilter('Length',63,'Method','LMS', ... 'StepSize',0.001,'LeakageFactor',0.99999, ... 'WeightsOutput','All'); % full Weights history w_actual = fir1(64,[0.5 0.75]); firfilt3 = dsp.FIRFilter('Numerator',w_actual); sinewave = dsp.SineWave('Frequency',0.01, ... 'SampleRate',1,'SamplesPerFrame',FrameSize); scope = timescope('TimeUnits','Seconds', ... 'YLimits',[-0.25 0.75],'BufferLength',2*FrameSize, ... 'ShowLegend',true,'ChannelNames', ... {'Coeff 33 Estimate','Coeff 34 Estimate','Coeff 35 Estimate', ... 'Coeff 33 Actual','Coeff 34 Actual','Coeff 35 Actual'});
Запустите одну систему координат и выведите полную историю адаптивных весов, w.
x = randn(FrameSize,1); % Input signal d = firfilt3(x) + sinewave(); % Noise + Signal [~,~,w] = lmsfilt3(x,d);
Каждая строка в w - набор весов, оцененных для соответствующей входной выборки. Каждый столбец в w приводит полную историю определенного веса. Постройте график фактического веса и всей истории 33-го, 34-го и 35-го веса. На графике можно увидеть, что предполагаемый выход веса в конечном счете сходится с фактическим весом, когда адаптивный фильтр получает входные выборки и продолжает адаптироваться.
idxBeg = 33; idxEnd = 35; scope([w(:,idxBeg:idxEnd), repmat(w_actual(idxBeg:idxEnd),FrameSize,1)])

Алгоритм фильтра LMS определяется следующими уравнениями.
Различные алгоритмы адаптивного фильтра LMS, доступные в этом системном объекте, определяются как:
LMS -- Решает уравнение Вайнера-Хопфа и находит коэффициенты фильтра для адаптивного фильтра.
Нормализованный LMS - нормализованное изменение LMS-алгоритма.
В Normalized LMS, для преодоления потенциальной числовой нестабильности в обновлении весов, в знаменателе была добавлена небольшая положительная константа, Для ввода с двойной точностью с плавающей точностью, Для входных параметров с одной точностью с плавающей точностью Для входных параметров с фиксированной точкой
Sign-Data LMS - Коррекция к весам фильтра при каждой итерации зависит от знака входа u (n).
где u (n) реально.
Sign-Error LMS - Коррекция, применяемое к текущим весам фильтра для каждой последующей итерации, зависит от знака ошибки, e (n).
Sign-Sign LMS - Коррекция, применяемая к текущим весам фильтра для каждой последующей итерации, зависит как от знака u (n), так и от знака e (n).
где u (n) реально.
Переменные следующие:
| Переменная | Описание |
|---|---|
|
n |
Текущий индекс времени |
|
u (n) |
Вектор буферизованных входных выборок на шаге n |
|
u * (n) |
Комплексный сопряженный вектор буферизованных входных выборок на шаге n |
|
w (n) |
Вектор оценки веса фильтра на шаге n |
|
y(n) |
Отфильтрованный выход на шаге n |
|
e(n) |
Ошибка расчета на шаге n |
|
d(n) |
Желаемый ответ на шаге n |
|
µ |
Размер шага адаптации |
α | Коэффициент утечки (0 < α ≤ 1) |
ε | Константа, которая исправляет любую потенциальную числовую нестабильность, которая возникает во время обновления весов. |
[1] Хейс, M.H. Статистическая цифровая обработка сигналов и моделирование. Нью-Йорк: John Wiley & Sons, 1996.
Указания и ограничения по применению:
Смотрите Системные объекты в Генерации кода MATLAB (MATLAB Coder).
The dsp.LMSFilter Системный объект поддерживает генерацию кода SIMD с помощью технологии Intel AVX2 в следующих условиях:
Method установлено в 'LMS' или 'Normalized LMS'.
WeightsOutput установлено в 'None' или 'Last'.
Входной сигнал является реальным.
Входной сигнал имеет тип данных single или double.
Технология SIMD значительно повышает эффективность сгенерированного кода.
Следующие схемы показывают типы данных, используемые в dsp.LMSFilter объект для сигналов с фиксированной точкой. Таблица результирующих определений переменных, используемых в схемах:
| Переменная | Определение |
|---|---|
u | Входной вектор |
W | Вектор весов фильтра |
µ | Размер шага |
e | Ошибка |
Q | Частный, |
Продукт u 'u | Тип данных продукта в Энергетической схеме |
Аккумулятор u 'u | Тип данных аккумулятора в Энергетической схеме |
Продукт W 'u | Тип данных продукта в схеме свертки |
Аккумулятор W 'u | Тип данных аккумулятора в схеме свертки |
Продукт | Тип данных продукта в Продукте размера шага и схемы ошибок |
Продукт | Тип данных продукта и аккумулятора в схеме обновления веса. 1 |
1Тип данных аккумулятора для этой величины автоматически устанавливается таким же, как и тип данных продукта. Информация о минимальном, максимальном и переполнении для этого аккумулятора регистрируется как часть информации о продукте. Autoscaling рассматривает этот продукт и аккумулятор как один тип данных.
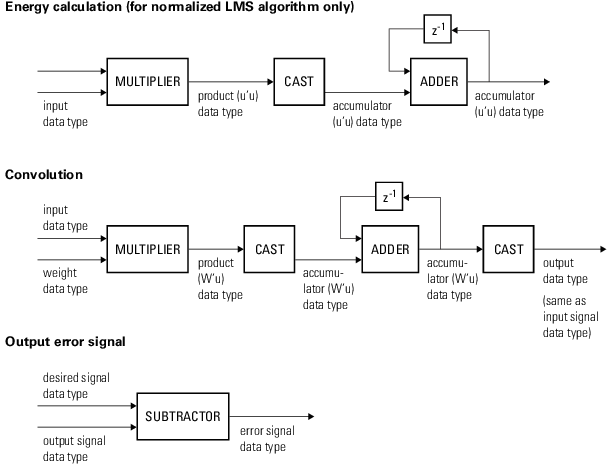
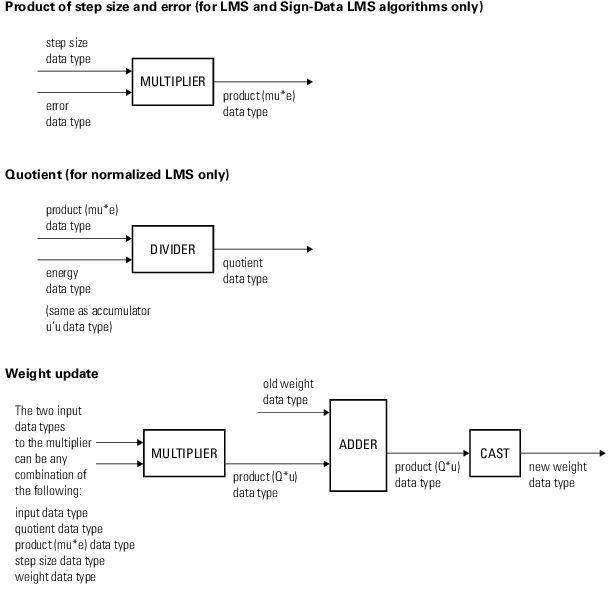
Можно задать тип данных свойств, весов, продуктов, частных и аккумуляторов в свойствах системного объекта. Входы, выходы и свойства системного объекта с фиксированной точкой должны иметь следующие характеристики:
Входной сигнал и требуемый сигнал должны иметь одинаковый размер слова, но их длины дробей могут различаться.
Размер шага и коэффициент утечки должны иметь одинаковый размер слова, но их длины могут различаться.
Сигнал выхода и сигнал ошибки имеют тот же размер слова и ту же длину дроби, что и требуемый сигнал.
Частный и выход продукта u 'u, W' u, , и операции должны иметь тот же размер слова, но их длины дробей могут различаться.
Тип данных аккумулятора операций u 'u и W' u должен иметь одинаковый размер слова, но их длины дробей могут различаться.
Выход умножителя находится в продукт типе выходных данных, если хотя бы один из входов в умножитель действителен. Если оба входов в умножитель являются комплексными, результат умножения находится в типе данных аккумулятора. Для получения дополнительной информации о выполненном комплексном умножении смотрите Типы данных умножения.
dsp.AdaptiveLatticeFilter | dsp.AffineProjectionFilter | dsp.BlockLMSFilter | dsp.FastTransversalFilter | dsp.FilteredXLMSFilter | dsp.FIRFilter | dsp.FrequencyDomainAdaptiveFilter | dsp.RLSFilterУ вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.