Рассмотрим стохастический процесс, принимающий значения в state space. Markov process развивается таким образом, который не зависит от пути, который ведет к текущему состоянию. То есть текущее состояние содержит всю информацию, необходимую для предсказания условных вероятностей будущих путей. Эта характеристика называется Markov property. Несмотря на то, что марковский процесс является специфическим типом стохастического процесса, он широко используется в моделировании изменений состояния. Специфика марковского процесса приводит к относительно полной теории.
Марковские процессы могут быть ограничены различными способами, что приводит к прогрессивно более кратким математическим формулировкам. Следующие условия являются примерами ограничений.
Пространство состояний может быть ограничено дискретным набором. Эта характеристика указывает на Markov chain. Вероятности перехода свойства Маркова «связывают» каждое состояние в цепи с следующим.
Если пространство состояний конечное, цепь finite-state.
Если процесс развивается в дискретных временных шагах, цепь discrete-time.
Если свойство Маркова не зависит от времени, цепь homogeneous.
Econometrics Toolbox™ включает dtmc объект модели, представляющий конечную, дискретную по времени, однородную марковскую цепь. Даже с ограничениями, dtmc объект имеет большую применимость. Он достаточно прочен, чтобы служить во многих сценариях моделирования в эконометрике, и математическая теория хорошо подходит для матричной алгебры MATLAB®.
Конечногосударственные марковские цепи имеют двойственную теорию: одну в матричном анализе и одну в дискретных графиках. Функции объекта dtmc объект подсвечивает эту двойственность. Функции позволяют вам перемещаться вперед и назад между числовым и графическим представлениями. Можно работать с инструментами, которые лучше всего подходят для конкретных аспектов исследования. В частности, традиционные методы собственного значения для определения структуры переходной матрицы соединены с визуализациями для отслеживания эволюции цепи через связанный с ней диграф.
Ключевая возможность любой марковской цепи является ее ограничивающим поведением. Эта функция особенно важна в эконометрических приложениях, где прогнозируемая эффективность модели зависит от того, имеет ли ее стохастический компонент четко определенное распределение, асимптотически. Функции объекта dtmc объект позволяет вам исследовать переходное и статическое поведение цепи и свойства, которые дают уникальный предел. Другие функции вычисляют предельное распределение и оценочные скорости сходимости, или mixing times.
Симуляция базового стохастического процесса подходящей марковской цепи является основополагающим для применения. Симуляция может принимать форму генерации случайной последовательности переходов состояний от начального состояния или от временной эволюции всего распределения состояний. Симуляция позволяет вам определить статистические характеристики цепи, которые могут быть не очевидны из ее спецификации или теории. В эконометрике марковские цепи становятся компонентами больших моделей переключения режимов, где они представляют сдвиги в экономическом окружении. The dtmc объект включает функции для симуляции и визуализации временной эволюции марковских цепей.
Любая конечная, дискретная по времени, однородная марковская цепь может быть представлена, математически, либо своей n -by - n переходной матрицей P, где n - количество состояний, либо её ориентированной графовой D. Хотя эти две представления эквивалентны - анализ, выполненный в одной области, приводит к эквивалентным результатам в другой - существуют значительные различия как в концепции аналитических вопросов, так и в получившихся алгоритмических решениях. Эта дихотомия лучше всего проиллюстрирована сравнением развития теории в [7], например, с разработками в [6] и [9]. Или, используя MATLAB, дихотомия может быть проиллюстрирована сравнением алгоритмов, основанных на graph объект и его функции с основной функциональностью в матричном анализе.
Полный график для конечного процесса имеет ребра и вероятности перехода между каждым узлом i и каждым другим узлом j. Узлы представляют состояния в марковской цепи. В D, если матричный элемент Pij равен 0, то краевые соединительные состояния i и j удаляется. Поэтому D показывает только feasible переходы среди состояний. Кроме того, D могут включать self-loops, указывающие ненулевые вероятности Pii перехода от i состояния назад к себе. Вероятности самоперехода известны как inertia или persistence состояний.
В D walk между состояниями i и j является последовательностью связанных состояний, которая начинается с i и заканчивается с j и имеет длину не менее двух. А path - прогулка без повторяющихся состояний. А circuit - это прогулка, в которой i = j, но нет других повторных состояний.
j состояния reachable, или accessible, от i состояния, обозначается , если есть прогулка от i до j. Состояния communicate, обозначенные , если каждый достижим от другого. Связь является отношением эквивалентности в пространстве состояний, разделяя его на сообщающиеся классы. В теории графиков состояния, которые передаются, называются strongly connected components. Для марковских процессов важные свойства отдельных состояний делятся всеми другими состояниями в сообщающемся классе, и так становятся свойствами самого класса. Эти свойства включают:
Recurrence - свойство доступности из всех состояний, которые достижимы. Это свойство эквивалентно асимптотической вероятности возврата, равной 1. Каждая цепь имеет по крайней мере один рекуррентный класс.
Transience - Свойство не быть повторяющимся, то есть возможность доступа к состояниям, из которых нет возврата. Это свойство эквивалентно асимптотической вероятности возврата, равной 0. Классы с переходностью не влияют на асимптотическое поведение.
Periodicity - свойство циклирования среди нескольких подклассов в классе и сохранения некоторой памяти о начальном состоянии. Период состояния является наибольшим общим делителем длин всех схем, содержащих состояние. Состояния или классы с периодом 1 являются апериодическими. Самоциклы на состояниях гарантируют апериодичность и формируют базис для lazy chains.
Важным свойством цепи в целом является irreducibility. Цепь неприводима, если цепь состоит из одного класса связи. Свойства состояния или класса становятся свойствами всей цепи, что упрощает описание и анализ. Обобщение является unichain, которая является цепью, состоящей из одного рекуррентного класса и любого количества переходных классов. Важные анализы, связанные с асимптотикой, могут быть сосредоточены на рецидивирующем классе.
График condensed, который формируется путем консолидации состояний каждого класса в один суперузел, упрощает визуальное понимание общей структуры. На этом рисунке один ориентированное ребро между суперузлами C1 и C2 соответствует уникальному направлению перехода между классами.
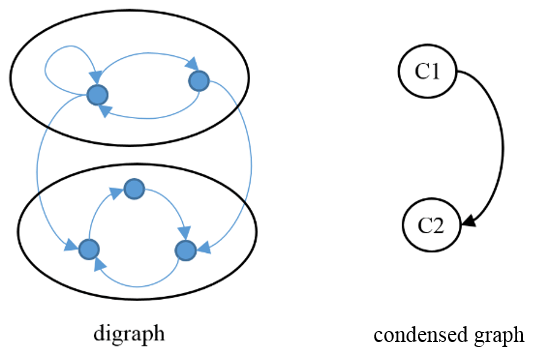
Конденсированный графиков показывает, что C1 является переходным и C2 является рекуррентным. Устаревшее C1 положительно, что подразумевает изменчивость. Поскольку C1 содержит самоцикл, он апериодичен. C2 периодически с периодом 3. Единичные состояния в трех циклах C2 являются, в более общем периодическом классе, сообщающимися подклассами. Цепь является редуцируемым унихаином. Представьте себе ориентированное ребро от C2 до C1. В этом случае C1 и C2 обмениваются классами, и они свертываются в один узел.
Ergodicity, желаемое свойство, сочетает неснижаемость с апериодичностью и гарантирует равномерное ограничивающее поведение. Поскольку неснижаемость по своей сути является свойством цепи, а не свойством класса, эргодичность также является свойством цепи. При использовании с унихаинами эргодичность означает, что уникальный рекуррентный класс является эргодичным.
С помощью этих определений можно суммировать фундаментальные теоремы существования и уникальности, связанные с 1-by n стационарными распределениями, где .
Если P правильно стохастический, то всегда имеет решение вектора вероятностей. Поскольку каждая строка P равна единице, P имеет правый собственный вектор с собственным значением единицы. В частности, e = 1 n, вектор n -by-1 таковых. Итак, у P также есть левый собственный вектор с собственным значением единицы. Как следствие теоремы Перрона-Фробениуса, является неотрицательной и может быть нормирована, чтобы получить вектор вероятности.
уникальна тогда и только тогда, когда P представляет собой унихаин. В целом, если цепь содержит k рекуррентных классов, π* = π*P имеет k линейно независимых решений. В этом случае Pm сходится как , но строки не идентичны.
Каждое начальное π 0 распределения сходится к тогда и только тогда, когда P представляет эргодический унихаин. В этом случае, является limiting distribution.
Теорема Перрона-Фробениуса - набор результатов, относящихся к собственным значениям неотрицательных, неприводимых матриц. Применительно к марковским цепям результаты можно подвести следующим образом. Для конечного унихейна P имеет одно собственное значение λ 1 = 1 (Perron-Frobenius eigenvalue) с сопутствующим неотрицательным левым собственным вектором (который может быть нормирован к вектору вероятностей) и правому собственному вектору e = 1 n. Другие собственные значения λi удовлетворять, i = 2, …, n. Если unichain или единственный рекуррентный класс unichain апериодичен, то неравенство строго. Когда существует периодичность k периода, на k круге модуля собственных значений в k корнях единства. Если unichain является эргодическим, то Pm сходится асимптотически к как . Ошибка переходит к 0, по крайней мере, так же быстро, как , где λs - собственное значение второй по величине, а q - кратность λs.
Скорость сходимости к зависит от second largest eigenvalue modulus (SLEM) . Ставка может быть выражена в терминах spectral gap, которая . Большие погрешности дают более быстрое сходимость. mixing time является характерным временем для отклонения от равновесия в общем расстоянии изменения. Поскольку сходимость экспоненциальна, время смешения для распада в множителе e1 является
Учитывая теоремы сходимости, время смешения должно рассматриваться в контексте эргодических уничаев.
Родственные теоремы в теории неотрицательных, неприводимых матриц дают удобные характеристики двух важнейших свойств для равномерной сходимости: редуктивности и эргодичности. Предположим Z что это indicator или zero pattern P, то есть матрица с таковыми вместо ненулевых записей в P. Затем P неприводимо тогда и только тогда, когда все записи положительны. Теорема Виландта [11] утверждает, что P эргодична тогда и только тогда, когда все записи Pm положительны для .
Теорема Перрона-Фробениуса и связанные с ней результаты неконструктивны для стационарного распределения . Существует несколько подходов к вычислению уникального лимитирующего распределения эргодической цепи.
Задайте return time Tii для состояния i как минимальное количество шагов для возврата к i состояния после запуска в i состояния. Кроме того, задайте mean return time τii как ожидаемое значение Tii. Затем, . Этот результат имеет много интуитивно понятного содержимое. Индивидуальное среднее время смешивания может быть оценено симуляцией Монте-Карло. Однако накладные расходы на моделирование и трудности оценки сходимости делают симуляцию Монте-Карло непрактичной как общий метод.
Потому что Pm приближается к матрице, все строки которой равны как любая строка «высокой степени» P аппроксимируется π*. Несмотря на то, что этот метод прост, он включает выбор допуска сходимости и соответственно большого m для каждой P. В целом, осложнения анализа времени смешения также делают эти расчеты непрактичными.
Линейная система может быть дополнен ограничением , в форме , где 1 n -by- n является n -by- n матрицей таковых. Используя ограничение, эта система становится
Система может быть эффективно решена с помощью оператора обратной косой черты MATLAB и численно стабильна, потому что эргодические P не могут иметь таковые по основной диагонали (в противном случае P были бы уменьшаемы). Этот метод рекомендуется в [5].
Поскольку является уникальным левым собственным вектором, сопоставленным с собственным значением Перрона-Фробениуса в P, сортировкой собственных значений и соответствующими собственными векторами, идентифицирует . Потому что ограничение не является частью задачи собственного значения, требует нормализации. Этот метод использует устойчивые числа MATLAB eigs function, и является подходом, реализованным asymptotics функция объекта dtmc объект.
Для любой марковской цепи конечноэтапный анализ может предположить ее асимптотические свойства и скорость смешения. Конечный анализ включает в себя расчет этих величин:
The hitting probability - вероятность попадания в любое состояние подмножества состояний A (цель), начиная с i состояний в цепи. Категорически, вероятности столкновения показывают, какие состояния достижимы из других состояний; > 0 означает, что целевой A достижим из i состояния. Если = 0, целевой A недоступен из i состояния, что означает, i состояние remote для целевого объекта. Если A образует повторяющийся класс, является absorption probability.
The expected first hitting time - долгосрочное среднее количество временных шагов, требуемых для достижения A в первый раз, начиная с i состояния. = ∞ означает одну из следующих альтернатив:
Начальное состояние i удалено для целевых A.
Начальное i remote-reachable для целевого A; то есть, > 0 и > 0, где B является повторяющимся классом, не содержащим состояний в A.
Если A образует повторяющийся класс, - ожидаемая absorption time.
Вектор вероятностей столкновения или ожидаемое первое время удара для цели, начиная с каждого состояния в марковской цепи, предполагает скорость смешения цепи.
[1] Diebold, F.X., and G.D. Rudebusch. Бизнес-циклы: длительность, динамика и прогнозирование. Princeton, NJ: Princeton University Press, 1999.
[2] Gallager, R.G. Stochastic Processes: Theory for Applications. Кембридж, Великобритания: Cambridge University Press, 2013.
[3] Gilks, W. R., S. Richardson, and D.J. Spiegelhalter. Марковская цепь Монте-Карло на практике. Бока Ратон: Чепмен и Холл/CRC, 1996.
[4] Haggstrom, O. Finite Markov Chains and Algorithmic Applications. Кембридж, Великобритания: Cambridge University Press, 2002.
[5] Гамильтон, Джеймс Д. Анализ временных рядов. Princeton, NJ: Princeton University Press, 1994.
[6] Хорн, Р. и К. Р. Джонсон. Матричный анализ. Кембридж, Великобритания: Cambridge University Press, 1985.
[7] Джарвис, Дж. П. и Д. Р. Шиер. «Граф-теоретический анализ конечных марковских цепей». В прикладном математическом моделировании: междисциплинарный подход. Бока Ратон: CRC Press, 2000.
[8] Маддала, Г. С., и И. М. Ким. Корни модулей, коинтеграция и структурное изменение. Кембридж, Великобритания: Cambridge University Press, 1998.
[9] Монтгомери, Дж. Математические модели социальных систем. Неопубликованная рукопись. Кафедра социологии, Университет Висконсина-Мэдисона, 2016.
[10] Norris, J. R. Markov Chains. Кембридж, Великобритания: Cambridge University Press, 1997.
[11] Wielandt, H. Topics in the Analytic Theory of Matrices. Лекционные заметки, подготовленные Р. Майером. Математический факультет Университета Висконсина-Мэдисона, 1967 год.
asymptotics | classify | eigplot | eigs | graphplot | isergodic | isreducible | lazy | mcmix