The dtmc Объекту среда предоставляет базовые инструменты для моделирования и анализа дискретных цепей Маркова. Объект поддерживает цепи с конечным числом состояний, которые развиваются за дискретное время с однородной по времени структурой перехода.
dtmc определяет каждую марковскую цепь с помощью NumStates-by- NumStates переходная матрица P, независимая от начального состояния x 0 или начального распределения состояний π 0. Можно задать P как правую стохастическую матрицу или матрицу эмпирических отсчётов.
Как правая стохастическая матрица:
Pij - неотрицательная вероятность перехода от i состояний к j состояний.
Каждая строка P равна 1.
описывает эволюцию распределения состояний от времени t ко времени t + 1.
Распределение состояний в момент t, πt является вектором-строкой длины NumStates.
Как матрица эмпирических отсчётов, Pij - это наблюдаемое количество раз i состояний, переходящих к j состояний. The dtmc объект нормирует строки P так, чтобы это была правая стохастическая матрица.
mcmix функция является альтернативным создателем объектов цепи Маркова; он генерирует цепь с заданным нулевым шаблоном и случайными вероятностями перехода. mcmix хорошо подходит для создания цепей с различным временем смешивания для проверка.
Чтобы визуализировать ориентированный граф, или диграф, связанный с цепью, используйте graphplot функция объекта. graphplot подобно тому, как plot функция объекта MATLAB®
digraph объект, но он включает дополнительную функциональность для анализа структуры марковской цепи. Настройки параметра подсвечивают коммуникационные классы (то есть strongly connected компоненты диграфа) и конкретные характеристики, влияющие на сходимость, такие как рецидив, переходность и периодичность. Можно выделить вероятности перехода в P путем раскраски ребер графика с помощью интенсивности тепловой карты.
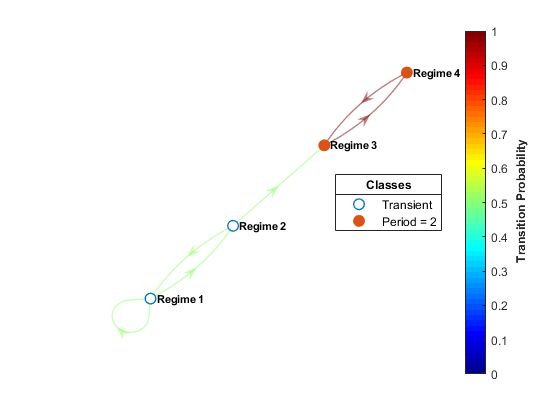
Чтобы визуализировать крупномасштабную структуру в цепи, graphplot может конденсировать классы передачи данных к репрезентативным узлам. Эта опция основана на condensation функция объекта digraph объект.
classify объект является численным аналогом подсветки классов в графике. classify возвращает характеристики сообщающихся классов, которые определяют ограничивающее поведение. Классификация состояний объединяет теоретико-графовые алгоритмы, такие как bfsearch (breadth-first search) функция объекта MATLAB graph объект, но с более прямыми матричными расчетами, специфичными для теории цепей Маркова. subchain способ позволяет извлечь конкретные классы связи из цепи для последующего анализа.
isreducible и isergodic функции объекта дают краткие сводные данные структуры цепи. Вместе они обеспечивают необходимые и достаточные условия для существования уникального ограничивающего распределения , где и для каждого начального распределения π 0. asymptotics вычисление функции объекта , если он существует, и оценивает время смешения с помощью собственного значения. eigplot Графики функций объекта собственные значения P. Этот рисунок показывает пример собственного значения, возвращенного eigplot.
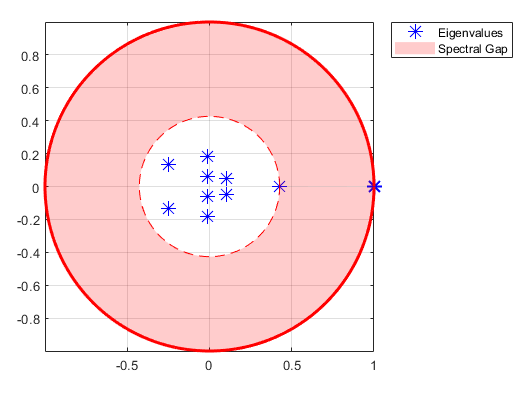
Одним из препятствий для сходимости является периодичность. lazy функция объекта устраняет периодичность путем регулирования инерции состояния (то есть путем взвешивания диагональных элементов P) для получения заданных количеств «лени» в цепи. Ограничение распределений не зависит от этих преобразований.
simulate и redistribute функции объекта обеспечивают реализацию процесса по мере его развития из заданного начального состояния или распределения. simplot и distplot функции объекта обеспечивают различные визуализации. Этот рисунок является примером графика распределения, показывающего эволюцию распределения состояний, начиная с равномерного начального распределения состояний.
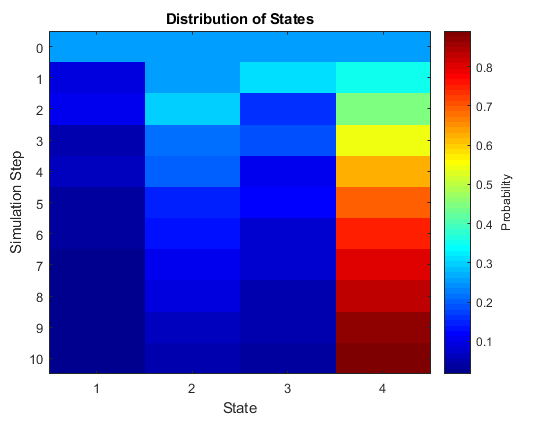
Можно начать создание объекта модели марковской цепи двумя способами:
Идентифицируйте соответствующие дискретные состояния в процессе, а затем оцените вероятности перехода среди них. В самом простом случае теория предполагает структуру цепи и P переходной матрицы. В этой ситуации вас интересует в первую очередь то, как теория разыгрывает на практике - то, что не всегда очевидно из теории. Как только вы знаете P, создайте объект марковской цепи, передав P в dtmc, который реализует теоретическую цепь.
Если у вас есть менее конкретная информация о процессе, то вы должны экспериментировать с различным количеством состояний и допустимыми шаблонами перехода, чтобы воспроизвести эмпирические результаты. mcmix функция обеспечивает понимание скелетной структуры цепи, которая может захватывать основные функции в данных. Посредством итерационного процесса можно настроить случайным образом сгенерированные матрицы P перехода в соответствии с целями моделирования.
Для построителя эконометрических моделей наиболее важным следствием выбора P является асимптотическое поведение цепи. Чтобы понять это поведение, идентифицируйте и отделите переходные состояния (те состояния, вероятности возврата которых уходят в нуль асимптотически) от рекуррентных состояний (тех состояний, вероятности возврата которых уходят в один асимптотически). Переходность и повторяемость являются свойствами, совместно используемыми всеми состояниями в связывающемся классе. Чтобы визуально определить, являются ли состояния переходными или рецидивирующими, передайте объект Марковской цепи в graphplot функция объекта и задайте 'ColorNodes',true. Кроме того, выходы classify функция объекта обеспечивает числовые инструменты для оценки. Этот рисунок является примером диграф с классифицированными узлами.
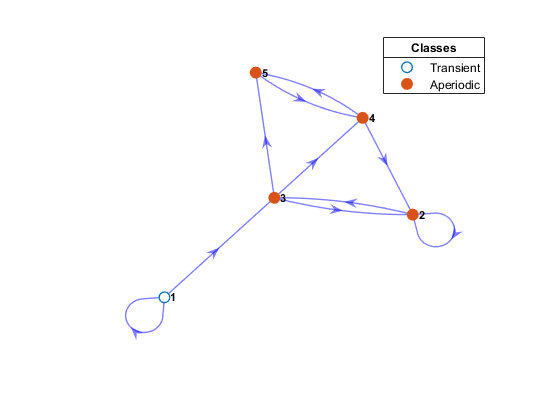
Конденсированное представление диграф упрощает эту оценку путем объединения каждого класса связи в «суперузел». В конденсированном график можно легко распознать переходность и рецидив по исходящей степени суперузла (выходная степень, больше 0, подразумевает переходность). Irreducible chains состоят из одного, обязательно повторяющегося, связывающегося класса. Unichains состоят из одного рекуррентного класса и любого количества спутниковых переходных классов. Unichains поддерживает желаемое ограничивающее поведение неприводимой цепи. Фактор конденсированного график часто является предшественником обрезки цепи нерелевантных переходных состояний. subchain функция обрезает цепи переходных классов. Этот рисунок является сгущенным видом диграф на предыдущем рисунке.
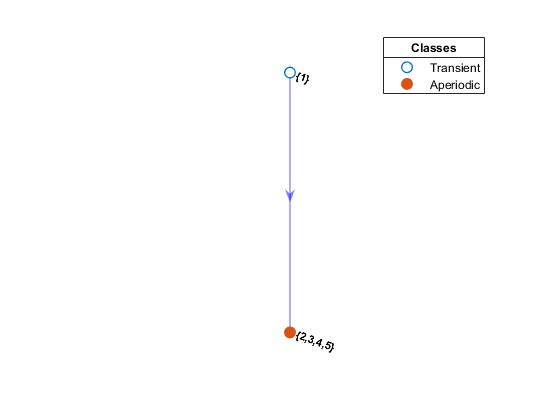
Два принципиальных препятствия для равномерного ограничивающего поведения:
Reducibility, существование более чем одного связывающегося класса
Periodicity, тенденция цикличности среди подклассов в пределах одного класса
Комбинация graphplot и classify функции объекта могут идентифицировать эти проблемы. Если цепь редуцируема, а не унихаин, обычно разделяют анализ на независимые рекуррентные классы или переформулируют цепь в целом. Если цепь является периодической (то есть содержит периодический повторяющийся класс), но общая структура захватывает основные детали приложения, lazy объект обеспечивает средство правовой защиты. Ленивые цепи возмущают диагональные элементы P, чтобы исключить периодичность, оставляя асимптотику незамеченной.
isreducible и isergodic функции объекта суммируют классификацию состояний. Каждая цепь имеет stationary distribution
, где в результате того, что P являются стохастическими и имеют собственное значение единицы. Если цепь неприводима, стационарное распределение уникально. Однако неснижаемость, хотя и достаточная, не является необходимым условием уникальности. Unichains также приводит к уникальному стационарному распределению, имеющему нулевую массу вероятностей в переходных состояниях. В этой связи классификационный анализ состояния необходим, потому что isreducible возвращает true только если цепь в целом состоит из одного класса связи. isreducible возвращает false для произвольных уничаев, в этом случае вы должны решить, являются ли переходные классы релевантной частью модели.
Ergodicity, или primitivity, является комбинацией неснижаемости и апериодичности. Эргодическая цепь имеет уникальное ограничение распределения, то есть π 0 сходится к для каждого начального распределения π 0. Можно определить, является ли цепь в целом эргодичной, используя isergodic. Функция идентифицирует эргодические унишены путем оценки единственного рекуррентного класса. Цепь является периодической, если она неприводима и не эргодична, то есть, если ~tfirreduc + ~tfergo = false, где tfirreduc и tfergo возвращаются isreducible и isergodic, соответственно.
Как только вы подтвердили, что цепь является эргодической, можно определить уникальное ограничение распределения при помощи asymptotics функция объекта. asymptotics возвращает ограничение распределения и оценку времени смешивания, которая является временной константой для распада переходного поведения. Теорема Перрона-Фробениуса для неприводимых неотрицательных матриц (см. [1]) полезна для интерпретации этих результатов. Любая стохастическая матрица имеет спектральный радиус единицы. Периодические матрицы периода k имеют k собственных значений, равномерно распределенных по модулю кругу в k корнях единства. Скорость распада переходных состояний определяется величиной самого большого собственного значения внутри модуля круга. eigplot функция объекта обеспечивает быструю визуализацию этой информации. Этот рисунок является собственным значением марковской цепи с периодом в три.
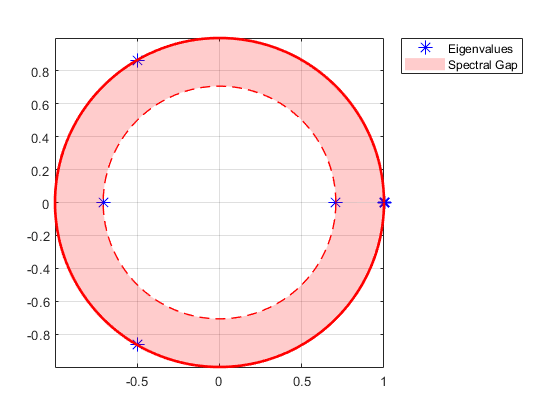
Независимо от асимптотических свойств цепи, можно изучить скорость ее смешения, применив конечношаговый анализ. hitprob и hittime функции возвращают вероятности столкновения и ожидаемое время первого столкновения для подмножества целевых состояний, начиная с каждого состояния в цепи. Обе функции опционально строят график с цветами узлов, определяющими вероятности столкновения или время. Этот рисунок показывает пример диграф с цветами узлов, определяющими ожидаемое время первого столкновения. Диграф также указывает, являются ли начальные состояния удаленными для цели.
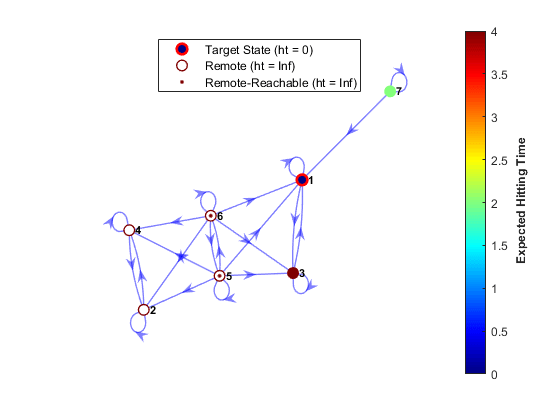
Симуляции и перераспределение позволяют вам генерировать статистическую информацию о цепи, которую трудно вывести непосредственно из теории. simulate и simplot функции объекта и redistribute и distplot функции объекта, обеспечивают вычислительные и графические инструменты для такого анализа. simulateдля примера генерирует независимые случайные прогулки по цепи. Как и в случае simulate и функции объектов в других частях Econometrics Toolbox™, ансамблевые средние значения зависимой статистики играют важную роль в прогнозировании. Передача simplot функция объекта предлагает несколько подходов к визуализации. Этот рисунок отображает долю состояний, посещенных после 100 случайных прогулок длиной 10 шагов через периодическую марковскую цепь на предыдущем рисунке.
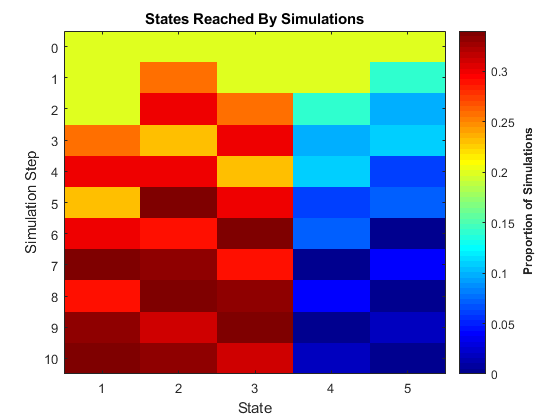
[1] Хорн, Р. и К. Р. Джонсон. Матричный анализ. Кембридж, Великобритания: Cambridge University Press, 1985.
bfsearch | condensation | graphplot | mcmix