Создайте регрессионные модели с ошибками ARIMA

Регрессионная модель по умолчанию со спецификациями ошибок ARIMA

Регрессионные модели с ошибками ARIMA имеют следующую форму (в обозначении оператора задержки):

$\begin{matrix} y_{t} = c + X_{t} β + u_{t} \\ a (L) A (L) {(1 - L)}^{D} (1 - L^{s}) u_{t} = b (L) B (L) ε_{t}, \end{matrix}$

где

t = 1..., T.
_yt - серия откликов.
_Xt - t строка X, которая является матрицей конкатенированных векторов данных предиктора. То есть _Xt является t наблюдения каждой серии предикторов.
c является регрессионной моделью точки пересечения.
β - коэффициент регрессии.
_ut - ряд нарушений порядка.
_εt - серия инноваций.
$L^{j} y_{t} = y_{t - j} .$
$a (L) = (1 - a_{1} L - ... - a_{p} L^{p}),$ который является p степени, несезональным авторегрессивным полиномом.
$A (L) = (1 - A_{1} L - ... - A_{p_{s}} L^{p_{s}}),$ который является _ps степени, сезонным авторегрессивным полиномом.
${(1 - L)}^{D},$ который является D степени, несезональным полиномом интегрирования.
$(1 - L^{s}),$ который является s степени, сезонным полиномом интегрирования.
$b (L) = (1 + b_{1} L + ... + b_{q} L^{q}),$ который является q степени, несезональным полиномом скользящего среднего значения.
$B (L) = (1 + B_{1} L + ... + B_{q_{s}} L^{q_{s}}),$ который является _qs степени, сезонным полиномом скользящего среднего значения.

Для простоты используйте сокращённое обозначение Mdl = regARIMA(p,D,q) задать регрессионную модель с ошибками ARIMA (p, D, q), где p, D, и q являются неотрицательными целыми числами. Mdl имеет следующие свойства по умолчанию.

Имя свойства	Тип данных свойств
`AR`	Длина `p` вектор камеры `NaN`s
`Beta`	Пустые векторные `[]` коэффициентов регрессии, соответствующих ряду предикторов
`D`	Неотрицательный скаляр, соответствующий D
`Distribution`	`"Gaussian"`, соответствующий распределению _εt
`Intercept`	`NaN`, соответствующий c
`MA`	Длина `q` вектор камеры `NaN`s
`P`	Количество членов AR плюс степень интегрирования, p + D
`Q`	Количество членов MA, q
`SAR`	Пустой вектор камеры
`SMA`	Пустой вектор камеры
`Variance`	`NaN`, соответствующий отклонению _εt
`Seasonality`	`0`, соответствующий s

Если вы задаете несезонные ошибки ARIMA, то

Свойства D и Q являются ли входы D и q, соответственно.
Свойства P = p + D, которая является степенью соединения, несезонного авторегрессионного полинома. Другими словами, P - степень продукта несезонного авторегрессионного полинома, a (L) и несезонного полинома интегрирования, (1 - L)^D.

Значения свойств P и Q указать, сколько предварительных наблюдений требуется программному обеспечению для инициализации временных рядов.

Можно изменять свойства Mdl использование записи через точку. Для примера, Mdl.Variance = 0.5 устанавливает отклонение инноваций равную 0,5.

Для максимальной гибкости в задании регрессионной модели с ошибками ARIMA используйте аргументы пары "имя-значение", чтобы, например, задать значение каждого из авторегрессивных параметров или задать мультипликативные сезонные условия. Для примера, Mdl = regARIMA('AR',{0.2 0.1}) задает регрессионую модель с AR (2) ошибками, и коэффициенты равны _a 1 = 0,2 и a 2 = 0,1.

Задайте модели regARIMA, используя аргументы в виде пар имя-значение

Можно задать только несезонные авторегрессионные и скользящие средние значения полиномиальные степени и несезонную степень интегрирования, используя краткое обозначение regARIMA(p,D,q). Некоторые задачи, такие как прогнозирование и симуляция, требуют, чтобы вы задали значения для параметров. Вы не можете задать значения параметров с помощью краткого обозначения. Для максимальной гибкости используйте аргументы пары "имя-значение", чтобы задать регрессионые модели с ошибками ARIMA.

Несезональная модель ошибки ARIMA может содержать следующие полиномы:

Степень p авторегрессивный полином a (<reservedrangesplaceholder5>) = 1 - <reservedrangesplaceholder4> 1 <reservedrangesplaceholder3> - <reservedrangesplaceholder2> 2 <reservedrangesplaceholder1> 2-...-<reservedrangesplaceholder0> L^p. Собственные значения a (L) должны лежать внутри модуля круга (т.е. a (L) должен быть стабильным полиномом).
Степень q полинома скользящего среднего b (L) = 1 + _b 1 L ₊ _b 2 L 2 +_... + bq L^q. Собственные значения b (L) должны лежать внутри модуля круга (т.е. b (L) должен быть обратимым полиномом).
Степень несезонального D полинома равна (1 - L)^D.

Следующая таблица содержит аргументы пары "имя-значение", которые вы используете, чтобы задать модель ошибки ARIMA (т.е. регрессионую модель с ошибками ARIMA, но без регрессионного компонента и точки пересечения):

\begin{matrix} y_{t} = u_{t} \\ a (L) (^{1 - L) D} = b (L) ε_{t} . \end{matrix}

(1)

Аргументы в виде пар имя-значение для несезонных моделей ошибок ARIMA

Имя	Соответствующий термин (ы) модели в уравнении 1	Когда задавать
`AR`	Несезонные коэффициенты AR: a 1, _a 2,..._, ap	Чтобы задать ограничения равенства для коэффициентов AR. Для примера задать коэффициенты AR в модели ошибки ARIMA $u_{t} = 0.8 u_{t - 1} - 0.2 u_{t - 2} + ε_{t},$ задайте `'AR',{0.8,-0.2}`. Вам нужно задать только ненулевые элементы `AR`. Если ненулевые коэффициенты находятся в неконсективных лагах, задайте соответствующие лаги, используя `ARLags`. Коэффициенты должны соответствовать стабильной AR- полинома.
`ARLags`	Лаги, соответствующие ненулевым, несезонным коэффициентам AR	`ARLags` не является свойством модели. Используйте этот аргумент как ярлык для определения `AR` когда ненулевые коэффициенты AR соответствуют неконсективным лагам. Для примера задать ненулевые коэффициенты AR в лагах 1 и 12, например, $u_{t} = a_{1} u_{t - 1} + a_{2} u_{t - 12} + ε_{t},$ задайте `'ARLags',[1,12]`. Использование `AR` и `ARLags` совместно для задания известных ненулевых коэффициентов AR при неконсективных лагах. Например, если в заданной модели ошибки AR (12) с _a 1 = 0,6 и _a 12 = -0,3, задайте `'AR',{0.6,-0.3},'ARLags',[1,12]`.
`D`	Степень несезонного дифференцирования, D	Чтобы задать степень несезонного дифференцирования, больше нуля. Для примера, чтобы задать одну степень дифференцирования, задайте `'D',1`. По умолчанию `D` имеет значение `0` (что означает отсутствие несезонного интегрирования).
`Distribution`	Распределение инновационного процесса, _εt	Используйте этот аргумент, чтобы задать распределение t студента. По умолчанию инновационное распределение `"Gaussian"`. Для примера, чтобы задать распределение t с неизвестными степенями свободы, задайте `'Distribution','t'`. Чтобы задать t инновационное распределение с известными степенями свободы, присвойте `Distribution` структуру с полями `Name` и `DoF`. Для примера для распределения t с девятью степенями свободы задайте `'Distribution',struct('Name','t','DoF',9)`.
`MA`	Несезонные коэффициенты MA: b 1, _b 2,..._, bq	Чтобы задать ограничения равенства для коэффициентов MA. Для примера задать коэффициенты MA в модели ошибки ARIMA $u_{t} = ε_{t} + 0.5 ε_{t - 1} + 0.2 ε_{t - 2},$ задайте `'MA',{0.5,0.2}`. Вам нужно задать только ненулевые элементы `MA`. Если ненулевые коэффициенты находятся в неконсективных лагах, задайте соответствующие лаги, используя `MALags`. Коэффициенты должны соответствовать инвертируемому полиному MA.
`MALags`	Лаги, соответствующие ненулевым, несезонным коэффициентам MA	`MALags` не является свойством модели. Используйте этот аргумент как ярлык для определения `MA` когда ненулевые коэффициенты MA соответствуют неконсективным лагам. Для примера задать ненулевые коэффициенты MA в лагах 1 и 4, например, $u_{t} = ε_{t} + b_{1} ε_{t - 1} + b_{4} ε_{t - 4},$ задайте `'MALags',[1,4]`. Использование `MA` и `MALags` вместе, чтобы задать известные ненулевые коэффициенты MA при неконсективных лагах. Например, если в заданной модели ошибки MA (4) _b 1 = 0,5 и b 4 = 0,2, `задайте 'MA',{0.4,0.2},'MALags',[1,4]`.
`Variance`	Скалярное отклонение, σ², инновационного процесса, _εt	Чтобы задать ограничения равенства для σ². Для примера, для модели ошибки ARIMA с известными инновациями отклонения 0,1, задайте `'Variance',0.1`. По умолчанию `Variance` имеет значение `NaN`.

Используйте аргументы пары "имя-значение" в следующей таблице в сочетании с аргументами в паре имя-значение для несезонных моделей ошибок ARIMA, чтобы задать регрессионные компоненты регрессионной модели с ошибками ARIMA:

\begin{matrix} y_{t} = c + X_{t} β + u_{t} \\ a (L) (^{1 - L) D} = b (L) ε_{t} . \end{matrix}

(2)

Аргументы в виде пар имя-значение для регрессионного компонента модели regARIMA

Имя	Соответствующий термин (ы) модели в уравнении 2	Когда задавать
`Beta`	Значения коэффициентов регрессии, соответствующие ряду предикторов, β	Используйте этот аргумент, чтобы задать значения коэффициентов ряда предикторов. Для примера используйте `'Beta',[0.5 7 -2]` определить $β = {[\begin{matrix} 0.5 & 7 & - 2 \end{matrix}]}^{'} .$ По умолчанию `Beta` - пустой вектор, `[]`.
`Intercept`	Точка пересечения» для регрессионной модели, c	Чтобы задать ограничения равенства для c. Для примера, для модели без точки пересечения термина задайте `'Intercept',0`. По умолчанию `Intercept` имеет значение `NaN`.

Если временные ряды имеют s сезонности, то

Степень _ps сезонный авторегрессивный полином A (<reservedrangesplaceholder4>) = 1 - _{<reservedrangesplaceholder3> 1 <reservedrangesplaceholder2>} - <reservedrangesplaceholder1> 2 <reservedrangesplaceholder0>² -... - _{_ApsL}^p_s.
Степень _qs сезонный полином скользящего среднего значения B (<reservedrangesplaceholder4>) 1 + _{<reservedrangesplaceholder3> 1 <reservedrangesplaceholder2>} + <reservedrangesplaceholder1> 2 <reservedrangesplaceholder0>² +... + _{_BqsL}^q_s.
Степень сезонного интегрирования s полином (1 - L^s).

Используйте аргументы пары "имя-значение" в следующей таблице в сочетании с аргументами в таблицах Аргументы в виде пар имя-значение для несезональных моделей ошибок ARIMA и Аргументы в виде пары имя-значение для регрессионного компонента модели regARIMA, чтобы задать регрессионую модель с мультипликативными сезонными ошибками ARIMA:

\begin{matrix} y_{t} = c + X_{t} β + u_{t} \\ a (L) (^{1 - L) D} A (L) (1 - L^{s}) u_{t} = b (L) B (L) ε_{t} . \end{matrix}

(3)

Аргументы в виде пар имя-значение для сезонных моделей ARIMA

Аргумент	Соответствующий термин (ы) модели в уравнении 3	Когда задавать
`SAR`	Сезонные коэффициенты AR: A 1, _A 2,..._,Aps	Чтобы задать ограничения равенства для сезонных коэффициентов AR. Использование `SARLags` для определения лагов ненулевых сезонных коэффициентов AR. Укажите лаги, связанные с сезонными полиномами, в периодичности наблюдаемых данных (например, 4, 8,... для ежеквартальных данных, или 12, 24,... для ежемесячных данных), а не как множители сезонности (например, 1, 2,...). Для примера задать модель ошибки ARIMA $(1 - 0.8 L) (1 - 0.2 L^{12}) u_{t} = ε_{t},$ задайте `'AR',0.8,'SAR',0.2,'SARLags',12`. Коэффициенты должны соответствовать стабильной сезонной AR- полинома.
`SARLags`	Лаги, соответствующие ненулевым сезонным коэффициентам AR, в периодичности ответов	`SARLags` не является свойством модели. Используйте этот аргумент при указании `SAR` для указания лагов ненулевых сезонных коэффициентов AR. Для примера задать модель ошибки ARIMA $(1 - a_{1} L) (1 - A_{12} L^{12}) u_{t} = ε_{t},$ задайте `'ARLags',1,'SARLags',12`.
`SMA`	Сезонные коэффициенты MA: B 1, _B 2,..._,Bqs	Чтобы задать ограничения равенства для сезонных коэффициентов MA. Использование `SMALags` для определения лагов ненулевых сезонных коэффициентов MA. Укажите лаги, связанные с сезонными полиномами, в периодичности наблюдаемых данных (например, 4, 8,... для ежеквартальных данных, или 12, 24,... для ежемесячных данных), а не как множители сезонности (например, 1, 2,...). Для примера задать модель ошибки ARIMA $u_{t} = (1 + 0.6 L) (1 + 0.2 L^{4}) ε_{t},$ задайте `'MA',0.6,'SMA',0.2,'SMALags',4`. Коэффициенты должны соответствовать инвертируемому сезонному полиному MA.
`SMALags`	Лаги, соответствующие ненулевым сезонным коэффициентам MA, в периодичности ответов	`SMALags` не является свойством модели. Используйте этот аргумент при указании `SMA` для указания лагов ненулевых сезонных коэффициентов MA. Для примера, чтобы задать модель $u_{t} = (1 + b_{1} L) (1 + B_{4} L^{4}) ε_{t},$ задайте `'MALags',1,'SMALags',4`.
`Seasonality`	Сезонная периодичность, s	Чтобы задать степень сезонного интегрирования s в сезонном дифференцированном полиноме _Δs = 1 - L^s. Для примера, чтобы определить периодичность сезонного интегрирования квартальных данных, укажите `'Seasonality',4`. По умолчанию `Seasonality` имеет значение `0` (что означает отсутствие периодичности или сезонного интегрирования).

Примечание

Вы не можете назначить значения свойствам P и Q. Для мультипликативных моделей ошибок ARIMA,

regARIMA устанавливает P равно p + D + _ps + s.
regARIMA устанавливает Q равно q + _qs

Задайте модели линейной регрессии, используя приложение Econometric Modeler

Можно задать переменные предиктора в компоненте регрессии, и структуру задержки модели ошибки и распределение инноваций, используя Econometric Modeler приложения. Приложение рассматривает все коэффициенты как неизвестные и оценочные.

В командной строке откройте приложение Econometric Modeler.

econometricModeler

Также откройте приложение из галереи Apps (см. Econometric Modeler).

В приложении можно увидеть все поддерживаемые модели, выбрав переменную временных рядов для ответа на панели Time Series. Затем на вкладке Econometric Modeler, в разделе Models, щелкните стреле, чтобы отобразить галерею моделей.

Раздел Regression Models содержит поддерживаемые регрессионные модели. Чтобы задать многофакторную линейную регрессию (MLR), выберите MLR. Чтобы задать регрессионные модели с ошибками ARMA, выберите RegARMA.

После выбора модели приложение отображает Type Диалоговое окно «Параметры модели», где Type является типом модели. Этот рисунок показывает диалоговое окно RegARMA Model Parameters.

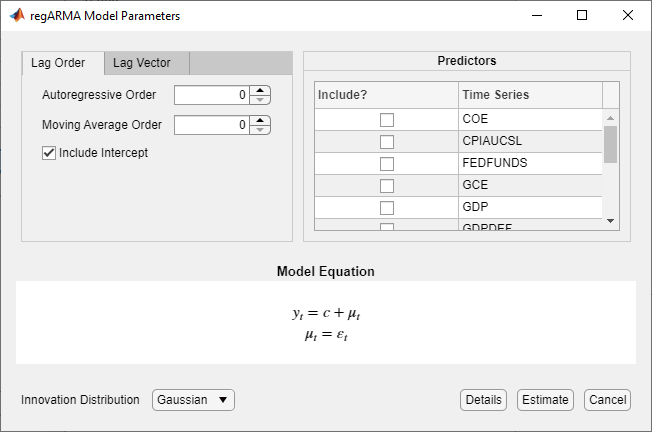
Регулируемые параметры зависят от модели Type. В целом регулируемые параметры включают:

Переменные предиктора для компонента линейной регрессии, перечисленные в разделе Predictors.
- Для регрессионных моделей с ошибками ARMA необходимо включить в модель по крайней мере один предиктор. Чтобы включить предиктор, установите соответствующий флажок в столбце Include?.
- Для моделей MLR можно снять все флажки в столбце Include?. В этом случае можно задать постоянную среднюю модель (модель только для перехвата), установив флажок Include Intercept. Или можно задать модель только для ошибок, сняв флажок Include Intercept.
Инновационное распределение и несезонные лаги для модели ошибки, для регрессионых моделей с ошибками ARMA.

Когда вы корректируете значения параметров, уравнение в Model Equation разделе изменяется так, чтобы оно совпадало с вашими спецификациями. Регулируемые параметры соответствуют входу и аргументам пары "имя-значение", описанным в предыдущих разделах и в regARIMA страница с описанием.

Для получения дополнительной информации об указании моделей с помощью приложения, смотрите Подбор моделей к данным и Определение полиномов оператора задержки в интерактивном режиме.

См. также

Приложения

Econometric Modeler

Объекты

regARIMA

Подробнее о

Регрессионные модели с ошибками временных рядов

Документация