harmonicГармоническая функция
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
harmonic(x)
harmonic(x) =![]() представляет гармоническую функцию.
представляет гармоническую функцию.
Гармоническая функция задана для всех сложных аргументов x кроме особых точек - 1, - 2, … (полюса первого порядка).
Для положительных целых чисел x, не больше, чем значение Pref::autoExpansionLimit (), гармоническая функция procudes гармонический номер![]() . Используйте
. Используйте expand(harmonic(x)), чтобы вычислить явный результат для целых чисел x, больше, чем Pref::autoExpansionLimit ().
Если x является значением с плавающей точкой, то значение с плавающей точкой возвращено.
Simplifcations реализованы для рациональных чисел x с |x | ≤ Pref:: autoExpansionLimit (). В частности, если x = numer(x)/k со знаменателями k = 1, 2, 3, 4, или 6, то явный результат вычислен и возвращен. Для других рациональных чисел функциональное уравнение![]() используется, чтобы получить результат с аргументом
используется, чтобы получить результат с аргументом x от интервала![]() .
.
Для рациональных чисел x с |x |> Pref:: autoExpansionLimit (), эти упрощения могут быть осуществлены через expand.
Некоторые явные формулы реализованы включая
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Специальное значение harmonic (∞) = ∞ реализовано.
Для всех других аргументов возвращен символьный вызов функции harmonic.
Атрибут expand использует функциональное уравнение![]() , отражательное правило
, отражательное правило![]() и формулу умножения Gauß для harmonic (k x) с некоторым целочисленным k, чтобы переписать
и формулу умножения Gauß для harmonic (k x) с некоторым целочисленным k, чтобы переписать harmonic(x). Смотрите Пример 3 и Пример 4.
Когда названо значением с плавающей точкой x, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
harmonic(3), harmonic(10), harmonic(3/2), harmonic(25/7)
![]()
harmonic(x + sqrt(2)), harmonic(infinity)
![]()
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
harmonic(-5.2), harmonic(27.0), harmonic(2.0 + 3.0*I)
![]()
harmonic сингулярен для отрицательных целых чисел:
harmonic(-2)
Error: Singularity. [harmonic]
Для положительных целых чисел и рациональных чисел x со знаменателями 2, 3, 4 и 6, соответственно, результат выражается с точки зрения PI и ln, если |x | <500:
harmonic(-5/2)
![]()
harmonic(13/3)
![]()
harmonic(101/6)
![]()
Для больших аргументов атрибут expand может использоваться, чтобы получить такие выражения:
harmonic(1001)
![]()
expand(%)
5337003...5042517 / 7128865...3520000
Функции diff, expand, float, limit и series обрабатывают выражения, включающие harmonic:
diff(harmonic(x^2 + 1), x), float(ln(3 + harmonic(sqrt(PI))))
![]()
expand(harmonic(2*x + 3))
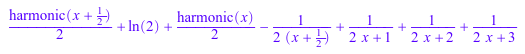
limit((x + 1)*harmonic(x), x = -1), limit(harmonic(x), x = infinity)
![]()
series(harmonic(x), x = 0)
![]()
series(harmonic(x), x = infinity, 3)
![]()
|
Арифметическое выражение.
x