Активные возвраты и ошибочная граница эффективности отслеживания

Предположим, что вы хотите идентифицировать эффективный набор портфелей, которые минимизируют отклонение различия в возвратах относительно данного целевого портфеля согласно даваемому ожидаемому избыточному возврату. Среднее и стандартное отклонение этого избыточного возврата часто называется активным возвратом и активным риском, соответственно. Активный риск иногда упоминается как ошибка отслеживания. Поскольку цель состоит в том, чтобы отследить данный целевой портфель максимально тесно, получившийся набор портфелей иногда упоминается как ошибочная граница эффективности отслеживания.

А именно, примите, что целевой портфель выражается как вектор веса индекса, такой, что индекс возвращается, ряд может быть выражен как линейная комбинация ликвидных активов. Этот пример иллюстрирует, как создать границу, которая минимизирует активный риск (отслеживающий ошибку) удовлетворяющий достижению данного уровня возврата. Таким образом, это вычисляет ошибочную границу эффективности отслеживания.

Один способ создать ошибочную границу эффективности отслеживания состоит в том, чтобы явным образом сформировать целевой ряд возврата и вычесть его из серии возврата отдельных активов. Этим способом вы задаете ожидаемое среднее значение и ковариацию активных возвратов, и вычисляете границу эффективности, удовлетворяющую обычным ограничениям портфеля.

Этот пример работает непосредственно со средним значением и ковариацией абсолютных (неприспособленных) возвратов, но преобразует ограничения от обычного абсолютного формата веса до активного формата веса.

Рассмотрите портфель пяти активов со следующими ожидаемыми доходами, стандартными отклонениями, и корреляционная матрица на основе абсолютного еженедельного актива возвращается.

NumAssets    =  5;

ExpReturn    = [0.2074  0.1971  0.2669  0.1323  0.2535]/100;

Sigmas       = [2.6570  3.6297  3.9916  2.7145  2.6133]/100;

Correlations = [1.0000  0.6092  0.6321  0.5833  0.7304
                0.6092  1.0000  0.8504  0.8038  0.7176
                0.6321  0.8504  1.0000  0.7723  0.7236
                0.5833  0.8038  0.7723  1.0000  0.7225
                0.7304  0.7176  0.7236  0.7225  1.0000];

Преобразуйте корреляции и стандартные отклонения к ковариационной матрице с помощью corr2cov.

ExpCovariance = corr2cov(Sigmas, Correlations);

Затем примите, что целевой портфель индекса является одинаково взвешенным портфелем, сформированным из этих пяти активов. Сумма весов индекса равняется 1, удовлетворяя стандартному полному инвестиционному бюджетному ограничению равенства.

Index = ones(NumAssets, 1)/NumAssets;

Сгенерируйте матрицу ограничений актива с помощью portcons. Матрица ограничений AbsConSet выражается в абсолютном формате (неприспособленный для индекса) и отформатирован как [A b], соответствие ограничениям формы A*w <= b. Каждая строка AbsConSet соответствует ограничению, и каждый столбец соответствует активу. Не позвольте короткую продажу, и полные инвестиции в каждый актив (нижние и верхние границы каждого актива 0 и 1, соответственно). В частности, обратите внимание, что первые две строки соответствуют бюджетному ограничению равенства; остающиеся строки соответствуют верхним/ниже инвестиционным границам.

AbsConSet = portcons('PortValue', 1, NumAssets, ... 
'AssetLims', zeros(NumAssets,1), ones(NumAssets,1));

Теперь преобразуйте абсолютные ограничения к активным ограничениям с abs2active.

ActiveConSet = abs2active(AbsConSet, Index);

Исследование абсолютных и активных ограничительных матриц показывает, что они отличаются только по последнему столбцу (столбцы, соответствующие b в A*w <= b).

[AbsConSet(:,end)  ActiveConSet(:,end)]

ans =

    1.0000         0
   -1.0000         0
    1.0000    0.8000
    1.0000    0.8000
    1.0000    0.8000
    1.0000    0.8000
    1.0000    0.8000
         0    0.2000
         0    0.2000
         0    0.2000
         0    0.2000
         0    0.2000

В частности, обратите внимание, что sum-one абсолютное ограничение бюджета становится суммой к нулю активное ограничение бюджета. Общее преобразование следующие:

$b_{a c t i v e} = b_{a b s o l u t e} - A \times I n d e x .$

Теперь создайте Portfolio возразите и постройте ошибочную границу эффективности отслеживания с 21 портфелем.

p = Portfolio('AssetMean', ExpReturn, 'AssetCovar', ExpCovariance);
p = p.setInequality(ActiveConSet(:,1:end-1), ActiveConSet(:,end));
[ActiveRisk, ActiveReturn] = p.plotFrontier(21);

plot(ActiveRisk*100, ActiveReturn*100, 'blue')
grid('on')
xlabel('Active Risk (Standard Deviation in Percent)')
ylabel('Active Return (Percent)')
title('Tracking Error Efficient Frontier')

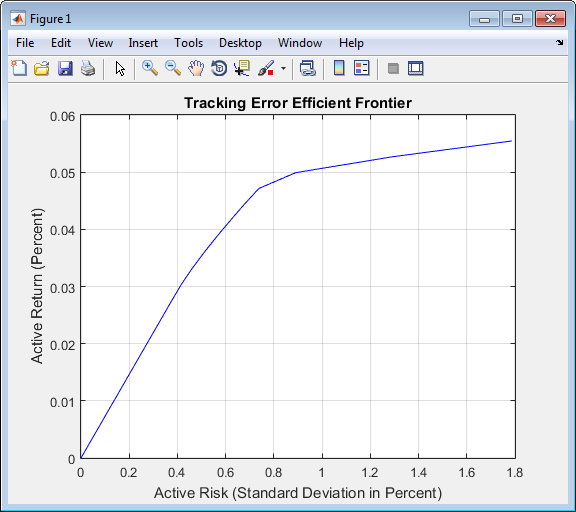
Особенно интересный нижний левый портфель вдоль границы. Этот zero-risk/zero-return портфель имеет практическое экономическое значение. Это представляет полные инвестиции в сам портфель индекса. Каждый ошибочный эффективный портфель отслеживания (каждая строка в массиве ActiveWeights) удовлетворяет активному ограничению бюджета, и таким образом представляет выделения портфельных инвестиций относительно портфеля индекса. Чтобы преобразовать эти выделения в абсолютные инвестиционные выделения, добавьте индекс в каждый эффективный портфель.

ActiveWeights = p.estimateFrontier(21);
AbsoluteWeights = ActiveWeights + repmat(Index, 1, 21);

Документация

Активные возвраты и ошибочная граница эффективности отслеживания

Смотрите также

Связанные примеры

Больше о

Документация Financial Toolbox

Поддержка