Exponenta Banner
exponenta event banner

pid2

Создайте диспетчера PID с 2 финансовыми департаментами в параллельной форме, преобразуйте в параллельную форму диспетчера PID с 2 финансовыми департаментами

свернуть все на странице

Синтаксис

C2 = pid2(Kp,Ki,Kd,Tf,b,c)
C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts)
C2 = pid2(sys)
C2 = pid2(___,Name,Value)

Описание

pid2 объекты контроллера представляют двухстепенные (2-DOF) ПИД контроллеры в параллельном виде. Использовать pid2 для создания pid2 объект контроллера из известных коэффициентов или для преобразования динамической модели системы в pid2 объект.

Контроллеры PID с двумя степенями свободы (2-DOF) включают взвешивание уставок на пропорциональном и производном уровнях. Контроллер PID 2-DOF может обеспечить быстрое отклонение возмущений без значительного увеличения превышения уставки. 2-DOF контроллеры PID также полезны для уменьшения влияния изменений опорного сигнала на управляющий сигнал. На следующем рисунке показана типичная архитектура управления с использованием контроллера 2-DOF PID.

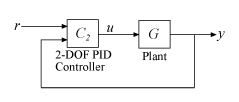
C2 = pid2(Kp,Ki,Kd,Tf,b,c) создает непрерывно-кратного диспетчера PID с 2 финансовыми департаментами с пропорциональной, составной, и производной прибылью Kp, Ki, и Kd и постоянная времени фильтра производных первого порядка Tf. Контроллер также имеет взвешивание уставки b на пропорциональном члене и взвешивании уставки c на деривативном термине. Соотношение между выходом (u) контроллера 2-DOF и его двумя входами (r и y) определяется следующим образом:

u = Kp (br − y) + Kis (r − y) + KdTfs + 1 (cr − y).

Это представление в параллельной форме. Если все коэффициенты вещественны, то результирующий C2 является pid2 объект контроллера. Если один или несколько из этих коэффициентов настраиваются (realp или genmat), то C2 является настраиваемым обобщенным состоянием-пространством (genss) объект модели.

C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts) создает дискретное время диспетчер PID с 2 финансовыми департаментами с типовым временем Ts. Соотношение между выходом контроллера и входами определяется:

u = Kp (br − y) + KiIF (z) (r − y) + KdTf + DF (z) (cr − y).

IF (z) и DF (z) являются дискретными формулами интегратора для интегратора и производного фильтра. По умолчанию

IF (z) = DF (z) = Tsz − 1.

Для выбора различных формул дискретного интегратора используйте IFormula и DFormula свойства. (Дополнительные сведения см. в разделе Свойства). Если DFormula = 'ForwardEuler' (значение по умолчанию) и Tf ≠ 0, затем Ts и Tf должны удовлетворять Tf > Ts/2. Это требование обеспечивает стабильный производный столб фильтра.

C2 = pid2(sys) преобразует динамическую систему sys в параллельную форму pid2 объект контроллера.

C2 = pid2(___,Name,Value) задает дополнительные свойства как пары, разделенные запятыми Name,Value аргументы.

Входные аргументы

Kp

Пропорциональный выигрыш.

Kp могут быть:

  • Действительное и конечное значение.

  • Массив вещественных и конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью tunableSurface.

Когда Kp = 0, контроллер не имеет пропорционального действия.

По умолчанию: 1

Ki

Интегральный выигрыш.

Ki могут быть:

  • Действительное и конечное значение.

  • Массив вещественных и конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью tunableSurface.

Когда Ki = 0, контроллер не имеет интегрального действия.

По умолчанию: 0

Kd

Выигрыш по производной.

Kd могут быть:

  • Действительное и конечное значение.

  • Массив вещественных и конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью tunableSurface.

Когда Kd = 0, контроллер не имеет производного действия.

По умолчанию: 0

Tf

Постоянная времени фильтра производной первого порядка.

Tf могут быть:

  • Действительное, конечное и неотрицательное значение.

  • Массив вещественных, конечных и неотрицательных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью tunableSurface.

Когда Tf = 0, контроллер не имеет фильтра для действия производной.

По умолчанию: 0

b

Взвешивание уставки на пропорциональном сроке.

b могут быть:

  • Действительное, неотрицательное и конечное значение.

  • Массив вещественных, неотрицательных, конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью tunableSurface.

Когда b = 0, изменения уставки не поступают непосредственно в пропорциональный член.

По умолчанию: 1

c

Взвешивание уставки по термину производной.

c могут быть:

  • Действительное, неотрицательное и конечное значение.

  • Массив вещественных, неотрицательных, конечных значений.

  • Настраиваемый параметр (realp) или обобщенная матрица (genmat).

  • Настраиваемая поверхность для настройки по расписанию усиления, созданная с помощью tunableSurface.

Когда c = 0, изменения уставки не поступают непосредственно в член производной.

По умолчанию: 1

Ts

Время выборки.

Создание дискретного времени pid2 контроллер, обеспечьте положительное реальное значение (Ts > 0). pid2 не поддерживает контроллеры дискретного времени с неопределенным временем выборки (Ts = -1).

Ts должно быть скалярным значением. В массиве pid2 контроллеры, каждый контроллер должен иметь одинаковые Ts.

По умолчанию: 0 (непрерывное время)

sys

Динамическая система SISO для преобразования в параллельную pid2 форма.

sys должна быть системой с двумя входами и одним выходом. sys должен представлять действительный контроллер 2-DOF PID, который может быть записан в параллельной форме с Tf  ≥ 0.

sys также может быть массивом динамических систем SISO.

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Использовать Name,Value синтаксис для задания формул числового интегрирования IFormula и DFormula дискретного времени pid2 или для установки других свойств объекта, таких как InputName и OutputName. Для получения информации о доступных свойствах pid2 объекты контроллера, см. раздел Свойства.

Выходные аргументы

C2

2-DOF Контроллер PID, возвращенный как pid2 объект контроллера, массив pid2 объекты контроллера, a genss объект или genss массив.

  • Если все коэффициенты имеют скалярные числовые значения, то C2 является pid2 объект контроллера.

  • Если один или несколько коэффициентов являются числовым массивом, C2 является массивом pid2 объекты контроллера. Тип контроллера (например, PI, PID или PDF) зависит от значений коэффициента усиления. Например, когда Kd = 0, но Kp и Ki ненулевые, C2 является PI-контроллером.

  • Если один или несколько коэффициентов являются настраиваемым параметром (realp), обобщенная матрица (genmat) или настраиваемой поверхности усиления (tunableSurface), то C2 является обобщенной государственно-пространственной моделью (genss).

Свойства

b, c

Вес уставки на пропорциональном и производном слагаемых соответственно. b и c значения являются действительными, конечными и положительными. При использовании pid2 команда, чтобы создать диспетчера PID с 2 финансовыми департаментами, b, и c входные аргументы, соответственно, устанавливают начальные значения этих свойств.

Kp, Ki, Kd

Усиление контроллера PID.

Пропорциональные, интегральные и производные коэффициенты усиления соответственно. Kp, Ki, и Kd значения действительны и конечны. При использовании pid2 команда, чтобы создать диспетчера PID с 2 финансовыми департаментами, Kp, Ki, и Kd входные аргументы, соответственно, устанавливают начальные значения этих свойств.

Tf

Постоянная времени фильтра производных.

Tf свойство сохраняет постоянную времени производного фильтра pid2 объект контроллера. Tf является действительным, конечным и больше или равным нулю. Когда Вы создаете диспетчера PID с 2 финансовыми департаментами, использующего pid2 команда, Tf входной аргумент задает начальное значение этого свойства.

IFormula

Формула дискретного интегратора IF (z) для интегратора дискретного времениpid2 диспетчер C2. Взаимосвязь между входами и выходом C2 задается:

u = Kp (br − y) + KiIF (z) (r − y) + KdTf + DF (z) (cr − y).

IFormula может принимать следующие значения:

  • 'ForwardEuler' - IF (z) = Tsz − 1.

    Эта формула лучше всего подходит для малого времени выборки, где предел Найквиста велик по сравнению с полосой пропускания контроллера. Для большего времени выборки, ForwardEuler формула может привести к нестабильности, даже при дискретизации системы, которая стабильна в течение непрерывного времени.

  • 'BackwardEuler' - IF (z) = Цз − 1.

    Преимущество BackwardEuler формула состоит в том, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда дает стабильный результат дискретного времени.

  • 'Trapezoidal' - IF (z) = Ts2z + 1z − 1.

    Преимущество Trapezoidal формула состоит в том, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда дает стабильный результат дискретного времени. Из всех доступных интеграционных формул Trapezoidal формула дает наиболее близкое совпадение между частотно-доменными свойствами дискретизированной системы и соответствующей системой непрерывного времени.

Когда C2 является контроллером непрерывного времени, IFormula является ''.

По умолчанию: 'ForwardEuler'

DFormula

Формула дискретного интегратора DF (z) для производного фильтра дискретного времениpid2 диспетчер C2. Взаимосвязь между входами и выходом C2 задается:

u = Kp (br − y) + KiIF (z) (r − y) + KdTf + DF (z) (cr − y).

DFormula может принимать следующие значения:

  • 'ForwardEuler' - DF (z) = Tsz − 1.

    Эта формула лучше всего подходит для малого времени выборки, где предел Найквиста велик по сравнению с полосой пропускания контроллера. Для большего времени выборки, ForwardEuler формула может привести к нестабильности, даже при дискретизации системы, которая стабильна в течение непрерывного времени.

  • 'BackwardEuler' - DF (z) = Цз − 1.

    Преимущество BackwardEuler формула состоит в том, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда дает стабильный результат дискретного времени.

  • 'Trapezoidal' - DF (z) = Ts2z + 1z − 1.

    Преимущество Trapezoidal формула состоит в том, что дискретизация стабильной системы непрерывного времени с использованием этой формулы всегда дает стабильный результат дискретного времени. Из всех доступных интеграционных формул Trapezoidal формула дает наиболее близкое совпадение между частотно-доменными свойствами дискретизированной системы и соответствующей системой непрерывного времени.

    Trapezoidal значение для DFormula недоступен для pid2 контроллер без фильтра производных (Tf = 0).

Когда C2 является контроллером непрерывного времени, DFormula является ''.

По умолчанию: 'ForwardEuler'

InputDelay

Временная задержка на входе системы. InputDelay всегда равно 0 для pid2 объект контроллера.

OutputDelay

Временная задержка на выходе системы. OutputDelay всегда равно 0 для pid2 объект контроллера.

Ts

Время выборки. Для моделей непрерывного времени Ts = 0. Для дискретно-временных моделей Ts - положительный скаляр, представляющий период выборки. Это значение выражается в единицах, указанных TimeUnit свойство модели. Модели контроллеров PID не поддерживают неопределенное время выборки (Ts = -1).

Изменение этого свойства не дискретизирует и не выполняет повторную выборку модели. Использовать c2d и d2c для преобразования между непрерывными и дискретными представлениями времени. Использовать d2d для изменения времени выборки системы дискретного времени.

По умолчанию: 0 (непрерывное время)

TimeUnit

Единицы измерения для переменной времени, времени выборки Tsи любые временные задержки в модели, указанные как одно из следующих значений:

  • 'nanoseconds'

  • 'microseconds'

  • 'milliseconds'

  • 'seconds'

  • 'minutes'

  • 'hours'

  • 'days'

  • 'weeks'

  • 'months'

  • 'years'

Изменение этого свойства не влияет на другие свойства и, следовательно, изменяет общее поведение системы. Использовать chgTimeUnit преобразование между единицами времени без изменения поведения системы.

По умолчанию: 'seconds'

InputName

Имя входного канала, определяемое как символьный вектор или массив ячеек 2 на 1 из символьных векторов. Это свойство используется для присвоения имени входным каналам модели контроллера. Например, присвойте имена setpoint и measurement к исходным данным диспетчера PID с 2 финансовыми департаментами модель C следующим образом.

C.InputName = {'setpoint';'measurement'};

Либо используйте автоматическое векторное расширение для назначения обоих входных имен. Например:

C.InputName = 'C-input';

Имена вводимых данных автоматически расширяются до {'C-input(1)';'C-input(2)'}.

Можно использовать сокращенную нотацию u см. InputName собственность. Например, C.u эквивалентно C.InputName.

Имена входных каналов имеют несколько применений, в том числе:

  • Идентификация каналов на дисплее модели и графиках

  • Указание точек соединения при соединении моделей

По умолчанию: {'';''}

InputUnit

Единицы входного канала, заданные как массив ячеек 2 на 1 символьных векторов. Это свойство используется для отслеживания единиц входного сигнала. Например, присвойте единицы измерения Volts к опорному входу и единицам концентрации mol/m^3 к входу измерения диспетчера PID с 2 финансовыми департаментами модель C следующим образом.

C.InputUnit = {'Volts';'mol/m^3'};

InputUnit не влияет на поведение системы.

По умолчанию: {'';''}

InputGroup

Группы входных каналов. Это свойство не требуется для моделей контроллеров PID.

По умолчанию: struct без полей

OutputName

Имя выходного канала, указанное как символьный вектор. Это свойство используется для присвоения имени выходному каналу модели контроллера. Например, присвойте имя control к выходу модели контроллера C следующим образом.

C.OutputName = 'control';

Можно использовать сокращенную нотацию y см. OutputName собственность. Например, C.y эквивалентно C.OutputName.

Имена входных каналов имеют несколько применений, в том числе:

  • Идентификация каналов на дисплее модели и графиках

  • Указание точек соединения при соединении моделей

По умолчанию: Пустой символьный вектор, ''

OutputUnit

Единицы выходного канала, заданные как символьный вектор. Это свойство используется для отслеживания единиц выходного сигнала. Например, присвойте единицу измерения Volts к выходу модели контроллера C следующим образом.

C.OutputUnit = 'Volts';

OutputUnit не влияет на поведение системы.

По умолчанию: Пустой символьный вектор, ''

OutputGroup

Группы выходных каналов. Это свойство не требуется для моделей контроллеров PID.

По умолчанию: struct без полей

Name

Имя системы, указанное как символьный вектор. Например, 'system_1'.

По умолчанию: ''

Notes

Любой текст, который требуется связать с системой, хранится в виде строки или массива ячеек символьных векторов. Свойство хранит данные любого типа. Например, если sys1 и sys2 являются динамическими моделями систем, можно задать их Notes следующие свойства:

sys1.Notes = "sys1 has a string.";
sys2.Notes = 'sys2 has a character vector.';
sys1.Notes
sys2.Notes
ans = 

    "sys1 has a string."


ans =

    'sys2 has a character vector.'

По умолчанию: [0×1 string]

UserData

Любой тип данных, который требуется связать с системой, указанный как любой тип данных MATLAB ®.

По умолчанию: []

SamplingGrid

Сетка выборки для массивов модели, заданная как структура данных.

Для массивов моделей, полученных путем выборки одной или нескольких независимых переменных, это свойство отслеживает значения переменных, связанные с каждой моделью в массиве. Эта информация появляется при отображении или печати массива модели. Эта информация используется для отслеживания результатов по независимым переменным.

Задайте имена полей структуры данных для имен переменных выборки. Задайте значения полей для значений выборочных переменных, связанных с каждой моделью в массиве. Все переменные выборки должны быть числовыми и скалярными значениями, а все массивы значений выборки должны соответствовать размерам массива модели.

Например, предположим, что создается массив линейных моделей 11 на 1, sysarr, делая снимки линейной изменяющейся во времени системы в моменты времени t = 0:10. В следующем коде хранятся выборки времени с линейными моделями.

 sysarr.SamplingGrid = struct('time',0:10)

Аналогично, предположим, что создается массив модели 6 на 9, M, путем независимой выборки двух переменных, zeta и w. Следующий код присоединяет (zeta,w) значения для M.

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

При отображении M, каждая запись в массиве включает в себя соответствующую zeta и w значения. 

M
M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

Для массивов моделей, созданных путем линеаризации модели Simulink ® в нескольких значениях параметров или рабочих точках, программа заполняетSamplingGrid автоматически со значениями переменных, которые соответствуют каждой записи в массиве. Например, команды Simulink Control Design™ linearize (Simulink Control Design) и slLinearizer (Simulink Control Design) заполнить SamplingGrid таким образом.

По умолчанию: []

Примеры

свернуть все

Открыть сценарий в реальном времени

Создайте контроллер 2-DOF непрерывного времени с пропорциональными и производными коэффициентами усиления и фильтр для члена производной. Для этого установите интегральный коэффициент усиления равным нулю. Задайте для других коэффициентов усиления и постоянной времени фильтра требуемые значения.

Kp = 1;
Ki = 0;   % No integrator
Kd = 3;
Tf = 0.1;
b = 0.5;    % setpoint weight on proportional term
c = 0.5;    % setpoint weight on derivative term
C2 = pid2(Kp,Ki,Kd,Tf,b,c)
C2 =
 
                         s    
  u = Kp (b*r-y) + Kd -------- (c*r-y)
                       Tf*s+1 

  with Kp = 1, Kd = 3, Tf = 0.1, b = 0.5, c = 0.5
 
Continuous-time 2-DOF PDF controller in parallel form.

На дисплее отображается тип контроллера, формула и значения параметров, а также проверяется отсутствие в контроллере члена интегратора.

Открыть сценарий в реальном времени

Создайте дискретное время диспетчер ПИ с 2 финансовыми департаментами, использующий трапециевидную формулу дискретизации. Укажите формулу с помощью Name,Value синтаксис.

Kp = 5;
Ki = 2.4;
Kd = 0;    
Tf = 0; 
b = 0.5;   
c = 0;      
Ts = 0.1;
C2 = pid2(Kp,Ki,Kd,Tf,b,c,Ts,'IFormula','Trapezoidal')
C2 =
 
                      Ts*(z+1)
  u = Kp (b*r-y) + Ki -------- (r-y)
                      2*(z-1) 

  with Kp = 5, Ki = 2.4, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

Настройка Kd = 0 задает PI-контроллер без производного члена. Как показано на дисплее, значения Tf и c не используются в этом контроллере. Дисплей также показывает, что для интегратора используется трапециевидная формула.

Открыть сценарий в реальном времени

Создайте 2-DOF PID-контроллер и задайте динамические свойства системы InputName и OutputName. Именование входов и выходов полезно, например, при соединении ПИД-контроллера с другими динамическими моделями систем с помощью connect команда.

C2 = pid2(1,2,3,0,1,1,'InputName',{'r','y'},'OutputName','u')
C2 =
 
                       1              
  u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
                       s              

  with Kp = 1, Ki = 2, Kd = 3, b = 1, c = 1
 
Continuous-time 2-DOF PID controller in parallel form.

У диспетчера PID с 2 финансовыми департаментами есть два исходных данных и одна продукция. Следовательно, 'InputName' свойство представляет собой массив, содержащий два имени, по одному для каждого ввода. На дисплее модели не отображаются входные и выходные имена для контроллера PID, но можно проверить значения свойств, чтобы увидеть их. Например, проверьте входное имя контроллера.

C2.InputName
ans = 2x1 cell
    {'r'}
    {'y'}
Открыть сценарий в реальном времени

Создайте сетку 2 на 3 из 2-DOF контроллеров PI с пропорциональным усилением от 1 до 2 в строках массива и интегральным усилением от 5 до 9 в столбцах.

Чтобы создать массив контроллеров PID, начните с массивов, представляющих выигрыш. 

Kp = [1 1 1;2 2 2];
Ki = [5:2:9;5:2:9];

При передаче этих массивов в pid2 команда возвращает массив контроллеров.

pi_array = pid2(Kp,Ki,0,0,0.5,0,'Ts',0.1,'IFormula','BackwardEuler');
size(pi_array)
2x3 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

Если предоставить скалярные значения для некоторых коэффициентов, pid2 автоматически расширяет их и присваивает одинаковое значение всем записям в массиве. Например, в этом примере Kd = Tf = 0, так что все записи в массиве являются контроллерами PI. Кроме того, все записи в массиве имеют b = 0.5.

Доступ к записям в массиве с помощью индексирования массива. Для динамических системных массивов первые два размера являются размерами ввода-вывода модели, а остальные - размерами массива. Поэтому следующая команда извлекает запись (2,3) в массиве.

pi23 = pi_array(:,:,2,3)
pi23 =
 
                       Ts*z 
  u = Kp (b*r-y) + Ki ------ (r-y)
                        z-1 

  with Kp = 2, Ki = 9, b = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PI controller in parallel form.

Можно также построить массив контроллеров PID с помощью stack команда. 

C2 = pid2(1,5,0.1,0,0.5,0.5);         % PID controller
C2f = pid2(1,5,0.1,0.5,0.5,0.5);      % PID controller with filter
pid_array = stack(2,C2,C2f);          % stack along 2nd array dimension

Эти команды возвращают массив контроллеров 1 на 2.

size(pid_array)
1x2 array of 2-DOF PID controller.
Each PID has 1 output and 2 inputs.

Все контроллеры PID в массиве должны иметь одинаковое время выборки, дискретные формулы интегратора и динамические свойства системы, такие как InputName и OutputName.

Открыть сценарий в реальном времени

Преобразование стандартной формы pidstd2 контроллер в параллельную форму.

Стандартная форма PID выражает действия контроллера в виде общего пропорционального усиления Kp, интегратор и производные константы времени Ti и Tdи делитель фильтра N. Можно преобразовать любой 2-DOF контроллер стандартной формы в параллельную форму с помощью pid2 команда. Например, рассмотрим следующий контроллер стандартной формы.

Kp = 2;
Ti = 3;
Td = 4;
N = 50;
b = 0.1;
c = 0.5;
C2_std = pidstd2(Kp,Ti,Td,N,b,c)
C2_std =
 
                       1      1                      s      
  u = Kp * [(b*r-y) + ---- * --- * (r-y) + Td * ------------ * (c*r-y)]
                       Ti     s                  (Td/N)*s+1 

  with Kp = 2, Ti = 3, Td = 4, N = 50, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in standard form

Преобразовать этот контроллер в параллельную форму с помощью pid2.

C2_par = pid2(C2_std)
C2_par =
 
                       1                s    
  u = Kp (b*r-y) + Ki --- (r-y) + Kd -------- (c*r-y)
                       s              Tf*s+1 

  with Kp = 2, Ki = 0.667, Kd = 8, Tf = 0.08, b = 0.1, c = 0.5
 
Continuous-time 2-DOF PIDF controller in parallel form.

График ответа подтверждает, что две формы эквивалентны.

bodeplot(C2_par,'b-',C2_std,'r--')
legend('Parallel','Standard','Location','Southeast')

Figure contains 4 axes. Axes 1 with title From: In(1) contains 2 objects of type line. These objects represent Parallel, Standard. Axes 2 contains 2 objects of type line. These objects represent Parallel, Standard. Axes 3 with title From: In(2) contains 2 objects of type line. These objects represent Parallel, Standard. Axes 4 contains 2 objects of type line. These objects represent Parallel, Standard.

Открыть сценарий в реальном времени

Преобразование динамической системы непрерывного времени, представляющей ПИД-контроллер, в параллельную pid форма.

Следующая динамическая система с интегратором и двумя нулями эквивалентна PID-контроллеру.

H (s) = 3 (s + 1) (s + 2) s.

Создать zpk модель Н. Затем использовать pid команда на получение H в терминах усиления PID Kp, Ki, и Kd.

H = zpk([-1,-2],0,3);
C = pid(H)
C =
 
             1          
  Kp + Ki * --- + Kd * s
             s          

  with Kp = 9, Ki = 6, Kd = 3
 
Continuous-time PID controller in parallel form.
Открыть сценарий в реальном времени

Преобразуйте дискретное время динамическая система, которая представляет диспетчера PID с 2 финансовыми департаментами с производным фильтром, чтобы быть параллельной pid2 форма.

Следующие матрицы состояния-пространства представляют контроллер дискретного времени 2-DOF PID с временем выборки 0,1 с.

A = [1,0;0,0.99];
B = [0.1,-0.1; -0.005,0.01];
C = [3,0.2];
D = [2.6,-5.2];
Ts = 0.1;
sys = ss(A,B,C,D,Ts);

При преобразовании sys для 2-DOF формы PID результат зависит от того, какие дискретные формулы интегратора задаются для преобразования. Например, используйте значение по умолчанию, ForwardEuler, как для интегратора, так и для производной.

C2fe = pid2(sys)
C2fe =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 5, Ki = 3, Kd = 2, Tf = 10, b = 0.5, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Теперь преобразуйте с помощью Trapezoidal формула.

C2trap = pid2(sys,'IFormula','Trapezoidal','DFormula','Trapezoidal')
C2trap =
 
                      Ts*(z+1)                     1         
  u = Kp (b*r-y) + Ki -------- (r-y) + Kd ------------------- (c*r-y)
                      2*(z-1)             Tf+Ts/2*(z+1)/(z-1)

  with Kp = 4.85, Ki = 3, Kd = 2, Tf = 9.95, b = 0.485, c = 0.5, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

На дисплее отображается разница в результирующих значениях коэффициентов и функциональной форме.

Открыть сценарий в реальном времени

Дискретизируйте непрерывно-кратного диспетчера PID с 2 финансовыми департаментами и определите составные и производные формулы фильтра.

Создайте контроллер непрерывного времени и дискретизируйте его с помощью метода удержания нулевого порядка c2d команда.

C2con = pid2(10,5,3,0.5,1,1);  % continuous-time 2-DOF PIDF controller
C2dis1 = c2d(C2con,0.1,'zoh')
C2dis1 =
 
                        Ts                   1     
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
                        z-1             Tf+Ts/(z-1)

  with Kp = 10, Ki = 5, Kd = 3.31, Tf = 0.552, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

На дисплее видно, что c2d вычисляет новые коэффициенты PID для контроллера дискретного времени.

Дискретные интеграторные формулы дискретизированного контроллера зависят от c2d метод дискретизации, как описано в Tips. Для zoh способ, оба IFormula и DFormula являются ForwardEuler.

C2dis1.IFormula
ans = 
'ForwardEuler'

C2dis1.DFormula
ans = 
'ForwardEuler'

Если требуется использовать формулы, отличные от формул, возвращаемых c2d, то вы можете непосредственно установить Ts, IFormula, и DFormula свойства контроллера до требуемых значений.

C2dis2 = C2con;
C2dis2.Ts = 0.1; 
C2dis2.IFormula = 'BackwardEuler';
C2dis2.DFormula = 'BackwardEuler';

Однако эти команды не вычисляют новые коэффициенты усиления PID для дискретизированного контроллера. Чтобы увидеть это, изучите C2dis2 и сравнить коэффициенты с C2con и C2dis1.

C2dis2
C2dis2 =
 
                       Ts*z                   1      
  u = Kp (b*r-y) + Ki ------ (r-y) + Kd ------------- (c*r-y)
                        z-1             Tf+Ts*z/(z-1)

  with Kp = 10, Ki = 5, Kd = 3, Tf = 0.5, b = 1, c = 1, Ts = 0.1
 
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.

Совет

  • Для проектирования PID-контроллера для конкретной установки используйте pidtune или pidTuner. Чтобы создать настраиваемый контроллер PID 2-DOF в качестве блока проектирования управления, используйте tunablePID2.

  • Чтобы разбить контроллер 2-DOF на два компонента управления SISO, такие как контроллер обратной связи и контроллер прямой связи, используйте getComponents.

  • Создание массивов pid2 объекты контроллера по:

    • Задание значений массива для одного или нескольких коэффициентов Kp, Ki, Kd, Tf, b, и c.

    • Задание массива динамических систем sys для преобразования в pid2 объекты контроллера.

    • Используя stack для построения массивов из отдельных контроллеров или массивов меньшего размера.

    • Передача массива моделей растений pidtune.

    В массиве pid2 контроллеры, каждый контроллер должен иметь одинаковое время выборки Ts и формулы дискретного интегратора IFormula и DFormula.

  • Чтобы создать или преобразовать контроллер стандартной формы, используйте pidstd2. Стандартная форма выражает действия диспетчера с точки зрения полной пропорциональной выгоды Kp, составные и производные времена Ti и Td и делитель фильтра N. Например, отношениями между исходными данными и продукцией непрерывно-разовой стандартной формы диспетчер PID с 2 финансовыми департаментами дают:

    u = Kp [(br − y) + 1Tis (r − y) + TdTdNs + 1 (cr − y)].

  • Существует два способа дискретизации непрерывного времени pid2 контроллер:

    • Используйте c2d команда. c2d вычисляет новые значения параметров для дискретизированного контроллера. Дискретные интеграторные формулы дискретизированного контроллера зависят от c2d используемый метод дискретизации, как показано в следующей таблице.

      c2d Метод дискретизацииIFormulaDFormula
      'zoh'ForwardEulerForwardEuler
      'foh'TrapezoidalTrapezoidal
      'tustin'TrapezoidalTrapezoidal
      'impulse'ForwardEulerForwardEuler
      'matched'ForwardEulerForwardEuler

      Для получения дополнительной информации о c2d методы дискретизации, см. c2d справочная страница. Для получения дополнительной информации о IFormula и DFormula, см. Свойства.

    • При необходимости использования различных формул дискретного интегратора можно выполнить дискретизацию контроллера путем непосредственного задания Ts, IFormula, и DFormula к требуемым значениям. (См., дискретизируют непрерывно-кратного диспетчера PID с 2 финансовыми департаментами.) Однако этот способ не вычисляет новые значения коэффициента усиления и постоянной фильтра для дискретизированного контроллера. Следовательно, этот метод может привести к худшему совпадению между непрерывным и дискретным временем.pid2 контроллеры, чем использование c2d.

См. также

| | | | | | | | |

Темы

Представлен в R2015b

Документация по панели инструментов системы управления

Поддержка