После наличия потенциальной модели для данных необходимо указать модель для MATLAB ®, чтобы продолжить анализ. Эконометрика Toolbox™ содержит объекты модели для хранения дискретно-временных эконометрических моделей.
Для одномерных рядов доступны следующие объекты модели:
arima - для интегрированных, авторегрессивных, моделей скользящего среднего (ARIMA), необязательно содержащих экзогенные предикторные переменные
garch - для обобщенных авторегрессивных моделей условной гетероскедастичности (GARCH)
egarch - для экспоненциальных моделей GARCH
gjr - для моделей Glosten-Jagannathan-Runkle
regARIMA - для регрессионных моделей с ошибками ARIMA
Для многомерных рядов доступны следующие объекты модели:
Econometrics Toolbox поддерживает одномерный байесовский анализ линейной регрессии. Объекты байесовской модели линейной регрессии определяют совместное предварительное распределение коэффициентов регрессии и дисперсии возмущений. Доступными объектами предыдущей модели являются:
conjugateblm - для нормальной-обратной-гамма-конъюгатной предшествующей модели. Коэффициенты регрессии и дисперсия возмущений являются зависимыми случайными переменными.
semiconjugateblm - для нормальной-обратной-гамма-полунъюгатной предыдущей модели. Коэффициенты регрессии и дисперсия возмущений являются независимыми случайными величинами.
diffuseblm - совместное предварительное распределение пропорционально обратной дисперсии возмущений.
empiricalblm - предварительное распределение сустава определяется случайной выборкой из заднего распределения сустава.
customblm - совместное предыдущее распределение указывается в объявленной пользовательской функции.
Для выбора байесовской переменной доступны следующие объекты предыдущей модели:
mixconjugateblm - для выполнения выбора переменной стохастического поиска (SSVS). Коэффициенты регрессии и дисперсия возмущений являются зависимыми случайными переменными (предыдущее и заднее распределения сопряжены).
mixsemiconjugateblm - для выполнения SSVS. Коэффициенты регрессии и дисперсия возмущений являются независимыми случайными переменными (предыдущее и заднее распределения являются полуконъюгатными).
lassoblm - для выполнения байесовской регрессии лассо.
Econometrics Toolbox поддерживает моделирование и анализ дискретных или непрерывных моделей Маркова. Доступными объектами модели являются:
dtmc - для дискретно-временных моделей цепи Маркова, характеризующихся матрицами перехода.
ssm - для непрерывных многомерных моделей состояния и пространства, необязательно содержащих экзогенные переменные предиктора
dssm - для непрерывных многомерных моделей состояния-пространства с диффузными начальными состояниями, необязательно содержащими экзогенные переменные предиктора
Чтобы создать объект модели, укажите форму модели для одной из функций модели (например, arima или garch). Функция создает объект модели соответствующего типа в рабочей области MATLAB, как показано на рисунке.
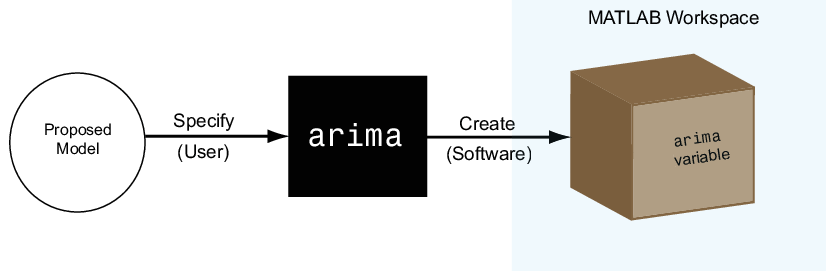
С объектами модели можно работать так же, как и с любой другой переменной в MATLAB. Например, можно назначить переменной объекта имя, просмотреть его в рабочей области MATLAB и отобразить его значение в окне команд, введя его имя.
На этом рисунке показана рабочая область, содержащая arima модель с именем Mdl.
Объект модели содержит всю информацию, необходимую для оценки, моделирования и прогнозирования эконометрических моделей. Эта информация включает в себя:
Параметрическая форма модели
Количество параметров модели (например, степень модели)
Распространение инноваций (Gaussian или Student's t)
Объем данных предварительной выборки, необходимый для инициализации модели
Такие части информации являются свойствами модели, которые хранятся в виде полей в объекте модели. Таким образом, объект модели напоминает структуру данных MATLAB (struct массив).
Пять типов моделей -arima, garch, egarch, gjr, и regARIMA- имеют свойства в соответствии с поддерживаемыми ими эконометрическими моделями. Каждое свойство имеет предопределенное имя, которое нельзя изменить.
Например, arima поддерживает условные средние модели (мультипликативные и аддитивные процессы AR, MA, ARMA, ARIMA и ARIMAX). Каждый arima объект модели имеет эти свойства, отображаемые с соответствующими именами.
| Имя свойства | Описание свойства |
|---|---|
Constant | Константа модели |
AR | Несезонные коэффициенты AR |
MA | Несезонные коэффициенты MA |
SAR | Сезонные коэффициенты AR (в мультипликативной модели) |
SMA | Сезонные коэффициенты МА (в мультипликативной модели) |
D | Степень несезонного дифференцирования |
Seasonality | Степень сезонной разницы |
Variance | Отклонение распределения инноваций |
Distribution | Параметрическое семейство распределения инноваций |
P | Объем данных предварительной выборки, необходимый для инициализации компонента AR модели |
Q | Объем данных предварительной выборки, необходимых для инициализации компонента MA модели |
Если объект модели существует в рабочей области, дважды щелкните его имя в окне Рабочая область (Workspace), чтобы открыть редактор переменных. Редактор переменных отображает все свойства модели и их имена.
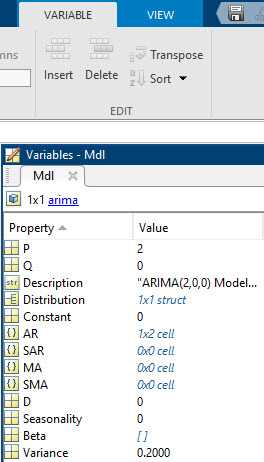
Обратите внимание, что в дополнение к имени каждое свойство имеет значение.
Укажите модель, назначив значения свойствам модели. Нет необходимости указывать значение для каждого свойства. Функция конструктора присваивает значения по умолчанию любым свойствам, которые не указаны или не могут быть заданы.
Совет
Рекомендуется знать значения свойств по умолчанию для любой создаваемой модели.
В дополнение к предопределенному имени каждое свойство модели имеет предопределенный тип данных. При назначении или изменении значения свойства оно должно соответствовать типу данных свойства.
Например, arima свойства имеют эти типы данных.
| Имя свойства | Тип данных свойства |
|---|---|
Constant | Скаляр |
AR | Массив ячеек |
MA | Массив ячеек |
SAR | Массив ячеек |
SMA | Массив ячеек |
D | Неотрицательное целое число |
Seasonality | Неотрицательное целое число |
Variance | Положительный скаляр |
Distribution | struct множество |
P | Неотрицательное целое число (нельзя указать) |
Q | Неотрицательное целое число (нельзя указать) |
Чтобы проиллюстрировать назначение значений свойств, рассмотрите возможность задания модели AR (2)
+ αt,
где нововведения являются независимыми и одинаково распределенными нормальными случайными величинами со средним значением 0 и дисперсией 0,2. Поскольку уравнение является условной средней моделью, используйте arima для создания объекта, представляющего модель. Назначьте значения свойствам модели с помощью аргументов пары имя-значение.
Эта модель имеет два коэффициента AR, 0,8 и -0,2. Назначение этих значений свойству AR как массив ячеек, {0.8,-0.2}. Присвоение значения 0.2 кому Variance, и 0 кому Constant. Вам не нужно присваивать значение Distribution поскольку распределение инноваций по умолчанию 'Gaussian'. Нет терминов MA, сезонных терминов или степеней интеграции, поэтому не присваивайте значения этим свойствам. Нельзя задать значения для свойств P и Q.
Таким образом, укажите модель следующим образом:
Mdl = arima('AR',{0.8,-0.2},'Variance',0.2,'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 2
D: 0
Q: 0
Constant: 0
AR: {0.8 -0.2} at lags [1 2]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 0.2
В выходных данных отображается значение созданной модели. Mdl. Обратите внимание, что свойство Seasonality отсутствует в выходных данных. Seasonality отображаются только для моделей с сезонной интеграцией. Однако свойство все еще присутствует, как показано в редакторе переменных.

Mdl имеет значения для каждого arima свойство, хотя спецификация включала только три. arima назначает значения по умолчанию для неопределенных свойств. Значения SAR, MA, и SMA пустые массивы ячеек, поскольку модель не имеет сезонных или MA-терминов. Значения D и Seasonality являются 0 потому что нет несезонных или сезонных разниц. arima наборы:
P равно 2, количество предварительных наблюдений, необходимых для инициализации модели AR (2).
Q равно 0 потому что в модели нет компонента MA (т.е. не требуются предварительные инновации).
В качестве другой иллюстрации рассмотрим задание модели GARCH (1,1)
αt,
где
α1αt-12
Предположим, следует стандартному нормальному распределению.
Эта модель имеет один коэффициент GARCH (соответствующий члену запаздывания дисперсии) и один коэффициент ARCH (соответствующий члену запаздывания в квадрате), оба с неизвестными значениями. Чтобы указать эту модель, введите:
Mdl = garch('GARCH',NaN,'ARCH',NaN)
Mdl =
garch with properties:
Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Offset: 0
Значение по умолчанию для члена константы также NaN. Параметры с NaN перед прогнозом или моделированием модели необходимо оценить или указать другое значение. Существует также краткий синтаксис для создания модели GARCH (1,1) по умолчанию:
Mdl = garch(1,1)
Mdl =
garch with properties:
Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Offset: 0
Сокращенный синтаксис возвращает модель GARCH с одним коэффициентом GARCH и одним коэффициентом ARCH, по умолчанию NaN значения.
Значения свойств в существующей модели доступны для извлечения. Работа с моделями напоминает работу с struct массивы, поскольку доступ к свойствам модели возможен с помощью точечной нотации. То есть введите имя модели, затем имя свойства, разделенное '.' (период).
Например, рассмотрим arima модель с данной спецификацией AR (2):
Mdl = arima('AR',{0.8,-0.2},'Variance',0.2,'Constant',0);
Отображение значения свойства AR для созданной модели введите:
arCoefficients = Mdl.AR
arCoefficients=1×2 cell array
{[0.8000]} {[-0.2000]}
AR является массивом ячеек, поэтому необходимо использовать синтаксис массива ячеек. Массивы ячеек коэффициентов индексируются с запаздыванием, поэтому вводится
secondARCoefficient = Mdl.AR{2}secondARCoefficient = -0.2000
возвращает коэффициент с запаздыванием 2. Новой переменной можно также присвоить любое значение свойства:
ar = Mdl.AR
ar=1×2 cell array
{[0.8000]} {[-0.2000]}
Можно также изменить свойства модели с помощью точечных обозначений. Например, рассмотрим эту спецификацию AR (2):
Mdl = arima('AR',{0.8,-0.2},'Variance',0.2,'Constant',0)
Mdl =
arima with properties:
Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 2
D: 0
Q: 0
Constant: 0
AR: {0.8 -0.2} at lags [1 2]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 0.2
Созданная модель имеет распределение гауссовых инноваций по умолчанию. Измените распределение инноваций на распределение Стьюдента с восемью степенями свободы. Тип данных для Distribution является struct массив.
Mdl.Distribution = struct('Name','t','DoF',8)
Mdl =
arima with properties:
Description: "ARIMA(2,0,0) Model (t Distribution)"
Distribution: Name = "t", DoF = 8
P: 2
D: 0
Q: 0
Constant: 0
AR: {0.8 -0.2} at lags [1 2]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 0.2
Переменная Mdl соответствующим образом обновляется.
Функции объектов - это функции, которые принимают объекты модели в качестве входных данных. В Econometrics Toolbox эти функции, представляющие шаги в рабочем процессе анализа эконометрики, принимают любой из объектов модели, включенных в панель инструментов:
estimate
forecast
simulate
Модель, которую можно подогнать к данным, имеет эти три общих метода, но объекты модели на панели инструментов могут иметь другие объектные функции.
Функции объекта могут различать объекты модели (например, arima модель в сравнении с garch модель). То есть некоторые объектные функции принимают различные необязательные входы и возвращают различные выходы в зависимости от типа вводимой модели.
Поиск страниц ссылок на функции объекта для определенной модели путем ввода, например, doc arima/estimate.
arima | conjugateblm | customblm | diffuseblm | dssm | dtmc | egarch | garch | gjr | lassoblm | mixconjugateblm | mixsemiconjugateblm | regARIMA | semiconjugateblm | ssm | varm | vecm