Оценка и проверка линейных моделей на основе данных с несколькими входами/одним выходом (MISO) для поиска модели, наилучшим образом описывающей динамику системы.
После завершения этого учебного пособия вы сможете выполнить следующие задачи с помощью командной строки:
Создание объектов данных для представления данных.
Постройте график данных.
Обработка данных путем удаления смещений из входного и выходного сигналов.
Оценка и проверка линейных моделей на основе данных.
Моделирование и прогнозирование выходных данных модели.
Примечание
В этом учебном пособии используются данные временной области для демонстрации способов оценки линейных моделей. Тот же рабочий процесс применяется к подгонке данных частотной области.
В данном учебном пособии используется файл данных co2data.mat, который содержит два эксперимента данных во временной области с двумя входами и одним выходом (MISO) из стационарного состояния, которое оператор нарушил из-за значений равновесия.
В первом эксперименте оператор ввел пульсовую волну на оба входа. Во втором эксперименте оператор ввел импульсную волну на первый вход и ступенчатый сигнал на второй вход.
Загрузите данные.
load co2data
Эта команда загружает следующие пять переменных в рабочую область MATLAB:
Input_exp1 и Output_exp1 - входные и выходные данные первого эксперимента соответственно.
Input_exp2 и Output_exp2 - входные и выходные данные второго эксперимента соответственно.
Time - временной вектор от 0 до 1000 минут, увеличивающийся с равными приращениями 0.5 мин.
Для обоих экспериментов входные данные состоят из двух столбцов значений. Первый столбец значений - скорость химического потребления (в килограммах в минуту), а второй столбец значений - текущая (в амперах). Выходные данные представляют собой один столбец скорости образования диоксида углерода (в миллиграммах в минуту).
Постройте график входных и выходных данных обоих экспериментов.
plot(Time,Input_exp1,Time,Output_exp1) legend('Input 1','Input 2','Output 1') figure plot(Time,Input_exp2,Time,Output_exp2) legend('Input 1','Input 2','Output 1')


На первом графике показан первый эксперимент, где оператор прикладывает пульсовую волну к каждому входу, чтобы возмутить его из его установившегося равновесия.
Второй график показывает второй эксперимент, где оператор подает импульсную волну на первый вход и шаговый сигнал на второй вход.
График данных, как описано в разделе «График входных/выходных данных», показывает, что входные и выходные данные имеют ненулевые значения равновесия. В этой части учебного пособия из данных вычитаются значения равновесия.
Причина вычитания средних значений из каждого сигнала заключается в том, что обычно строятся линейные модели, описывающие отклики на отклонения от физического равновесия. При стационарных данных разумно предположить, что средние уровни сигналов соответствуют такому равновесию. Таким образом, можно искать модели вокруг нуля без моделирования уровней абсолютного равновесия в физических единицах.
Увеличьте изображение графиков, чтобы увидеть, что самый ранний момент, когда оператор применяет возмущение к входам, наступает через 25 минут установившихся условий (или после первых 50 выборок). Таким образом, среднее значение первых 50 образцов представляет условия равновесия.
Для удаления значений равновесия из входов и выходов в обоих экспериментах используйте следующие команды:
Input_exp1 = Input_exp1-... ones(size(Input_exp1,1),1)*mean(Input_exp1(1:50,:)); Output_exp1 = Output_exp1-... mean(Output_exp1(1:50,:)); Input_exp2 = Input_exp2-... ones(size(Input_exp2,1),1)*mean(Input_exp2(1:50,:)); Output_exp2 = Output_exp2-... mean(Output_exp2(1:50,:));
Идентификация системы Toolbox™ объектов данных, iddata и idfrdинкапсулировать значения данных и свойства данных в один объект. Для удобного управления этими объектами данных как отдельными объектами можно использовать команды панели инструментов идентификации системы.
В этой части учебного пособия создаются два iddata объекты, по одному для каждого из двух экспериментов. Для оценки модели используются данные эксперимента 1, а для проверки модели - данные эксперимента 2. Работа выполняется с двумя независимыми наборами данных, поскольку один набор данных используется для оценки модели, а другой - для проверки модели.
Примечание
Если два независимых набора данных недоступны, можно разделить один набор данных на две части, предполагая, что каждая часть содержит достаточно информации для адекватного представления динамики системы.
Образцы данных должны быть уже загружены в рабочую область MATLAB ®, как описано в разделе Загрузка данных в рабочую область MATLAB.
Используйте эти команды для создания двух объектов данных, ze и zv :
Ts = 0.5; % Sample time is 0.5 min
ze = iddata(Output_exp1,Input_exp1,Ts);
zv = iddata(Output_exp2,Input_exp2,Ts);
ze содержит данные из эксперимента 1 и zv содержит данные из эксперимента 2. Ts - время выборки.
iddata конструктор требует три аргумента для данных временной области и имеет следующий синтаксис:
data_obj = iddata(output,input,sampling_interval);
Просмотр свойств iddata объект, используйте get команда. Например, введите эту команду, чтобы получить свойства оценочных данных:
get(ze)
ans =
struct with fields:
Domain: 'Time'
Name: ''
OutputData: [2001x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [2001x2 double]
u: 'Same as InputData'
InputName: {2x1 cell}
InputUnit: {2x1 cell}
Period: [2x1 double]
InterSample: {2x1 cell}
Ts: 0.5000
Tstart: []
SamplingInstants: [2001x0 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []
Дополнительные сведения о свойствах этого объекта данных см. в разделе iddata справочная страница.
Для изменения свойств данных можно использовать точечную нотацию или set команда. Например, чтобы назначить имена каналов и единицы измерения, маркирующие оси печати, введите следующий синтаксис в окне команд MATLAB:
% Set time units to minutes ze.TimeUnit = 'min'; % Set names of input channels ze.InputName = {'ConsumptionRate','Current'}; % Set units for input variables ze.InputUnit = {'kg/min','A'}; % Set name of output channel ze.OutputName = 'Production'; % Set unit of output channel ze.OutputUnit = 'mg/min'; % Set validation data properties zv.TimeUnit = 'min'; zv.InputName = {'ConsumptionRate','Current'}; zv.InputUnit = {'kg/min','A'}; zv.OutputName = 'Production'; zv.OutputUnit = 'mg/min';
Вы можете проверить, что InputName имущество ze изменяется или «index» в это свойство:
ze.inputname;
Совет
Имена свойств, например InputUnit, не чувствительны к регистру. Можно также сокращать имена свойств, которые начинаются с Input или Output путем замены u для Input и y для Output в имени свойства. Например, OutputUnit эквивалентно yunit.
Можно создавать графики iddata с использованием plot команда.
Постройте график оценочных данных.
plot(ze)

Нижние оси показывают входные данные ConsumptionRate и Current, а верхние оси показывают выходные данные ProductionRate .
Постройте график данных проверки в новом окне рисунка.
figure % Open a new MATLAB Figure window plot(zv) % Plot the validation data

Увеличьте изображение графиков, чтобы увидеть, что процесс эксперимента усиливает первый вход ( ConsumptionRate ) в 2 раза и усиливает второй вход (Current ) в 10 раз.
Прежде чем начать, создайте новый набор данных, который содержит только первые 1000 образцов исходных наборов данных оценки и проверки, чтобы ускорить вычисления.
Ze1 = ze(1:1000); Zv1 = zv(1:1000);
Дополнительные сведения об индексировании в iddata см. соответствующую справочную страницу.
Частотный отклик и ступенчатый отклик - непараметрические модели, которые помогают понять динамические характеристики системы. Эти модели не представлены компактной математической формулой с регулируемыми параметрами. Вместо этого они состоят из таблиц данных.
В этой части учебного пособия эти модели оцениваются с использованием набора данных. ze. Вы должны уже создать ze, как описано в разделе Создание объектов iddata.
Графики ответов из этих моделей показывают следующие характеристики системы:
Отклик от первого входа к выходу может быть функцией второго порядка.
Отклик от второго входа на выход может быть функцией первого порядка или избыточной.
Продукт System Identification Toolbox предоставляет три функции для оценки частотной характеристики:
Использовать spa для оценки частотной характеристики.
Ge = spa(ze);
Постройте график частотной характеристики как график Боде.
bode(Ge)

Пики амплитуды на частоте 0,54 рад/мин, что предполагает возможное резонансное поведение (комплексные полюса) для первой комбинации «вход-выход» - ConsumptionRate кому Production .
На обоих графиках фаза быстро сворачивается, что предполагает временную задержку для обеих комбинаций ввода/вывода.
Чтобы оценить ступенчатую характеристику из данных, сначала оцените непараметрическую модель импульсной характеристики (КИХ-фильтр) из данных, а затем постройте график ее ступенчатой характеристики.
% model estimation Mimp = impulseest(Ze1,60); % step response step(Mimp)

Отклик шага для первой комбинации ввода/вывода предполагает превышение, что указывает на наличие в физической системе режима с пониженным демпфированием (сложных полюсов).
Отклик шага от второго входа к выходу не показывает превышения, что указывает либо отклик первого порядка, либо отклик более высокого порядка с реальными полюсами (избыточный отклик).
График шага-отклика показывает ненулевую задержку в системе, которая согласуется с быстрым фазовым скатыванием, полученным на графике Боде, созданном в разделе Оценка эмпирического ответа шага.
Чтобы определить параметрические модели черного ящика, необходимо указать задержку ввода/вывода как часть порядка модели.
Если вы не знаете задержки ввода/вывода для вашей системы из эксперимента, вы можете использовать программное обеспечение System Identification Toolbox для оценки задержки.
В случае систем с одним входом можно прочитать задержку на графике импульса-отклика. Однако в случае систем с несколькими входами, например, в данном учебном пособии, вы не сможете определить, какие входные данные вызвали первоначальное изменение выходных данных, и вы можете использовать delayest вместо этого команда.
Команда оценивает временную задержку в динамической системе, оценивая модель ARX низкого порядка, дискретного времени с диапазоном задержек, а затем выбирая задержку, соответствующую наилучшему соответствию.
Структура модели ARX является одной из простейших параметрических структур черного ящика. В дискретном времени структура ARX представляет собой разностное уравнение со следующей формой:
(t − nk − nb + 1) + e (t)
y (t) представляет выходной сигнал в момент времени t, u (t) представляет входной сигнал в момент времени t, na - число полюсов, nb - число параметров b (равно числу нулей плюс 1), nk - количество выборок до того, как вход повлияет на выход системы (называется задержкой или временем покоя модели), и e (t) - возмущение белого шума.
delayest предполагает, что na = nb =2 и что шум e является белым или незначительным и оценивает nk.
Чтобы оценить задержку в этой системе, введите:
delayest(ze)
ans =
5 10
Этот результат включает в себя два числа, потому что есть два входа: предполагаемая задержка для первого входа 5 выборки данных, и предполагаемая задержка для второго входного сигнала 10 выборки данных. Потому что время выборки для экспериментов 0.5 min, это соответствует 2.5 -min задержка до того, как первый вход повлияет на выход, и 5.0 -min задержка до того, как второй вход повлияет на выход.
Существует два альтернативных метода оценки временной задержки в системе:
Постройте график времени входных и выходных данных и считайте разницу во времени между первым изменением входных и первых изменений выходных данных. Этот метод практичен только для системы с одним входом/одним выходом; в случае систем с несколькими входами вы не сможете определить, какие входные данные вызвали первоначальное изменение выходных данных.
Постройте график импульсной характеристики данных с доверительной областью 1 стандартного отклонения. Можно оценить временную задержку, используя время, когда импульсная характеристика сначала находится вне доверительной области.
Порядок модели - это одно или несколько целых чисел, определяющих сложность модели. В общем случае порядок модели связан с количеством полюсов, количеством нулей и задержкой отклика (время в терминах количества отсчетов до того, как выход ответит на вход). Конкретное значение порядка модели зависит от структуры модели.
Чтобы вычислить параметрические модели черного ящика, необходимо указать порядок моделей в качестве входных данных. Если порядок системы неизвестен, его можно оценить.
После выполнения шагов в этом разделе вы получите следующие результаты:
Для первой комбинации «вход-выход»: na = 2, nb = 2 и задержка nk = 5.
Для второй комбинации «вход-выход»: na = 1, nb = 1 и задержка nk = 10.
Позже можно исследовать различные структуры модели, задав значения порядка модели, которые являются незначительными вариациями вокруг этих начальных оценок.
В этой части учебного пособия используется struc, arxstruc, и selstruc оценить и сравнить простые полиномиальные (ARX) модели для диапазона порядков моделей и задержек, а также выбрать наилучшие порядки на основе качества модели.
В следующем списке описаны результаты использования каждой команды:
struc создает матрицу комбинаций порядка модели для заданного диапазона значений na, nb и nk.
arxstruc получает выходные данные из strucсистематически оценивает модель ARX для каждого порядка моделей и сравнивает выходной сигнал модели с измеренным выходным сигналом. arxstruc возвращает функцию потерь для каждой модели, которая является нормированной суммой квадратичных ошибок прогнозирования.
selstruc получает выходные данные из arxstruc и открывает окно Выбор структуры модели ARX (ARX Model Structure Selection), которое напоминает следующий рисунок, чтобы помочь выбрать порядок модели.
Этот график используется для выбора модели наилучшего вписывания.
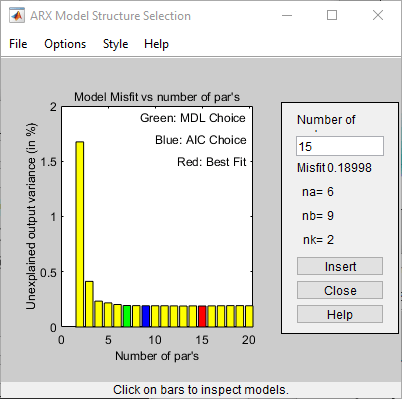
Горизонтальная ось - общее число параметров - na + nb.
Вертикальная ось, называемая необъяснимой выходной дисперсией (в%), является частью выходного сигнала, не объясненной моделью - ошибка прогнозирования модели ARX для количества параметров, показанных на горизонтальной оси.
Ошибка прогнозирования представляет собой сумму квадратов разностей между выводом данных проверки достоверности и прогнозируемым выводом модели на один шаг вперед.
nk - задержка.
Три прямоугольника выделены на графике зеленым, синим и красным цветом. Каждый цвет указывает тип критерия наилучшего соответствия следующим образом:
Красный - наилучшая подгонка минимизирует сумму квадратов разницы между выводом данных проверки и выводом модели. Этот прямоугольник указывает общее наилучшее вписывание.
Зеленый - наилучшая подгонка минимизирует критерий Rissanen MDL.
Синий - наилучшая подгонка минимизирует критерий Akaike AIC.
В этом учебном пособии значение «Необъяснимая выходная дисперсия» (в%) остается приблизительно постоянным для общего числа параметров от 4 до 20. Такое постоянство указывает на то, что производительность модели не улучшается при более высоких порядках. Таким образом, модели низкого порядка могут одинаково хорошо соответствовать данным.
Примечание
При использовании одного и того же набора данных для оценки и проверки используйте критерии MDL и AIC для выбора заказов модели. Эти критерии компенсируют переоборудование, вызванное использованием слишком большого количества параметров. Дополнительные сведения об этих критериях см. в разделе selstruc справочная страница.
В этом учебном пособии представлены два входа в систему и один выход, а модельные заказы для каждой комбинации ввода/вывода оцениваются независимо. Можно либо оценить задержки на двух входах одновременно, либо на одном входе одновременно.
Имеет смысл попробовать следующие комбинации порядка для первой комбинации ввода/вывода:
na =2:5
nb =1:5
nk =5
Это происходит потому, что непараметрические модели, оцененные при оценке моделей импульсной характеристики, показывают, что отклик для первой комбинации ввода/вывода может иметь отклик второго порядка. Аналогично, при оценке задержек в системе с несколькими входами задержка для этой комбинации ввода/вывода оценивалась как 5.
Для оценки порядка модели для первой комбинации ввода/вывода:
Использовать struc для создания матрицы возможных заказов модели.
NN1 = struc(2:5,1:5,5);
Использовать selstruc для вычисления функций потерь для моделей ARX с заказами в NN1.
selstruc(arxstruc(ze(:,:,1),zv(:,:,1),NN1))
Примечание
ze(:,:,1) выбирает первый вход в данные.
Эта команда открывает интерактивное окно Выбор структуры модели ARX (ARX Model Structure Selection).
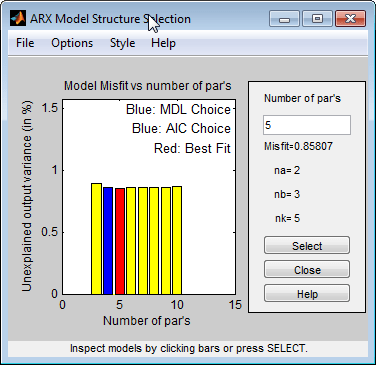
Примечание
Критерии Rissanen MDL и Akaike AIC дают эквивалентные результаты и оба обозначаются синим прямоугольником на графике.
Красный прямоугольник представляет наилучшую общую аппроксимацию для na = 2, nb = 3 и nk = 5. Перепад высот между красными и синими прямоугольниками незначителен. Поэтому можно выбрать комбинацию параметров, которая соответствует самому низкому порядку модели и самой простой модели.
Щелкните синий прямоугольник, а затем нажмите кнопку Выбрать, чтобы выбрать эту комбинацию порядков:
na =2
nb =2
nk =5
Для продолжения нажмите любую клавишу в окне команд MATLAB.
Имеет смысл попробовать следующие комбинации порядка для второй комбинации ввода/вывода:
na =1:3
nb =1:3
nk =10
Это происходит потому, что непараметрические модели, оцененные при оценке моделей импульсной характеристики, показывают, что отклик для второй комбинации ввода/вывода может иметь отклик первого порядка. Аналогично, при оценке задержек в системе с несколькими входами задержка для этой комбинации ввода/вывода оценивалась как 10.
Для оценки порядка модели для второй комбинации ввода/вывода:
Использовать struc для создания матрицы возможных заказов модели.
NN2 = struc(1:3,1:3,10);
Использовать selstruc для вычисления функций потерь для моделей ARX с заказами в NN2.
selstruc(arxstruc(ze(:,:,2),zv(:,:,2),NN2))
Эта команда открывает интерактивное окно Выбор структуры модели ARX (ARX Model Structure Selection).
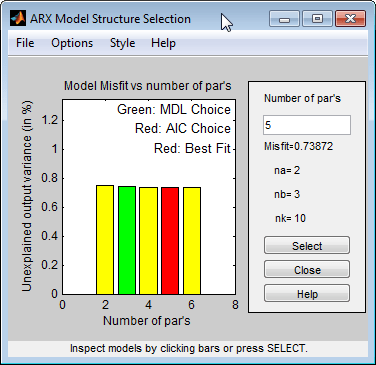
Примечание
AIC Akaike и общие критерии наилучшего соответствия дают эквивалентные результаты. Оба обозначаются одним и тем же красным прямоугольником на графике.
Разность высот между всеми прямоугольниками незначительна, и все эти порядки моделей приводят к сходной производительности модели. Поэтому можно выбрать комбинацию параметров, которая соответствует самому низкому порядку модели и самой простой модели.
Щелкните желтый прямоугольник в крайнем левом углу, а затем нажмите кнопку «Выбрать», чтобы выбрать нижний порядок: na = 1, nb = 1 и nk = 10.
Для продолжения нажмите любую клавишу в окне команд MATLAB.
В этой части учебного пособия оценивается функция непрерывного переноса времени. Необходимо подготовить данные, как описано в разделе Подготовка данных. Для определения заказов модели можно использовать следующие результаты оценочных заказов модели:
Для первой комбинации ввода/вывода используйте:
Два полюса, соответствующие na=2 в модели ARX.
Задержка 5, соответствующая nk=5 образцы (или 2,5 минут) в модели ARX.
Для второй комбинации ввода/вывода используйте:
Один полюс, соответствующий na=1 в модели ARX
Задержка 10, соответствующая nk=10 образцы (или 5 минут) в модели ARX.
Можно оценить передаточную функцию этих заказов с помощью tfest команда. Для оценки можно также выбрать просмотр отчета о ходе выполнения, установив Display опция для on в наборе опций, созданном tfestOptions команда.
Opt = tfestOptions('Display','on');
Собрать заказы модели и задержки в переменные для передачи в tfest.
np = [2 1]; ioDelay = [2.5 5];
Оцените передаточную функцию.
mtf = tfest(Ze1,np,[],ioDelay,Opt);

Просмотрите коэффициенты модели.
mtf
mtf =
From input "ConsumptionRate" to output "Production":
-1.382 s + 0.0008305
exp(-2.5*s) * -------------------------
s^2 + 1.014 s + 5.447e-12
From input "Current" to output "Production":
5.93
exp(-5*s) * ----------
s + 0.5858
Continuous-time identified transfer function.
Parameterization:
Number of poles: [2 1] Number of zeros: [1 0]
Number of free coefficients: 6
Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using TFEST on time domain data "Ze1".
Fit to estimation data: 78.92%
FPE: 14.22, MSE: 13.97
Отображение модели показывает более 85% соответствия данным оценки.
В этой части учебного пособия создается график, сравнивающий фактические выходные данные и выходные данные модели с помощью compare команда.
compare(Zv1,mtf)

Сравнение показывает примерно 60% подгонки.
Используйте resid для оценки характеристик остатков.
resid(Zv1,mtf)

Остатки показывают высокую степень автокорреляции. Это не является неожиданным, поскольку модель mtf не имеет каких-либо компонентов для отдельного описания характера шума. Для моделирования как измеренной динамики ввода-вывода, так и динамики возмущений необходимо использовать структуру модели, которая содержит элементы для описания шумовой составляющей. Вы можете использовать bj, ssest и procest команды, создающие модели структур полинома, состояния-пространства и процесса соответственно. Эти структуры, среди прочего, содержат элементы для фиксации шумового поведения.
В этой части учебного пособия оценивается функция переноса низкого порядка с непрерывным временем (модель процесса). продукт System Identification Toolbox поддерживает модели непрерывного времени, содержащие не более трех полюсов (которые могут содержать неполноценные полюса), один ноль, элемент задержки и интегратор.
Необходимо подготовить данные, как описано в разделе Подготовка данных.
Для определения заказов модели можно использовать следующие результаты оценочных заказов модели:
Для первой комбинации ввода/вывода используйте:
Два полюса, соответствующие na = 2 в модели ARX.
Задержка 5, соответствующая nk = 5 выборок (или 2,5 минут) в модели ARX.
Для второй комбинации ввода/вывода используйте:
Один полюс, соответствующий na = 1 в модели ARX.
Задержка 10, соответствующая nk = 10 выборок (или 5 минут) в модели ARX.
Примечание
Поскольку между количеством нулей, оцененных моделью ARX с дискретным временем, и ее аналогом с непрерывным временем нет никакой связи, оценка количества нулей отсутствует. В этом учебном пособии можно задать один ноль для первой комбинации ввода/вывода и не использовать ноль для второй комбинации вывода.
Используйте idproc для создания двух структур модели, по одной для каждой комбинации ввода/вывода:
midproc0 = idproc({'P2ZUD','P1D'}, 'TimeUnit', 'minutes');
Массив ячеек {'P2ZUD','P1D'} определяет структуру модели для каждой комбинации ввода/вывода:
'P2ZUD' представляет передаточную функцию с двумя полюсами ( P2 ), один ноль ( Z ), недампированные (комплексно-сопряженные) полюса ( U ) и задержка ( D ).
'P1D' представляет передаточную функцию с одним полюсом ( P1 ) и задержка ( D ).
В примере также используется TimeUnit для указания единицы времени.
Просмотрите две результирующие модели.
midproc0
midproc0 =
Process model with 2 inputs: y = G11(s)u1 + G12(s)u2
From input 1 to output 1:
1+Tz*s
G11(s) = Kp * ---------------------- * exp(-Td*s)
1+2*Zeta*Tw*s+(Tw*s)^2
Kp = NaN
Tw = NaN
Zeta = NaN
Td = NaN
Tz = NaN
From input 2 to output 1:
Kp
G12(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = NaN
Tp1 = NaN
Td = NaN
Parameterization:
{'P2DUZ'} {'P1D'}
Number of free coefficients: 8
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
Значения параметров устанавливаются в NaN потому что они еще не оценены.
Задайте для свойства временной задержки объекта модели значение 2.5 мин и 5 мин для каждой пары вход/выход в качестве начальных предположений. Кроме того, установите верхний предел задержки, поскольку доступны хорошие начальные догадки.
midproc0.Structure(1,1).Td.Value = 2.5; midproc0.Structure(1,2).Td.Value = 5; midproc0.Structure(1,1).Td.Maximum = 3; midproc0.Structure(1,2).Td.Maximum = 7;
Примечание
При установке ограничений задержки необходимо указать задержки с точки зрения фактических единиц времени (в данном случае минут), а не количества выборок.
procest является итеративным оценщиком моделей процессов, что означает, что он использует итеративный нелинейный алгоритм наименьших квадратов для минимизации функции затрат. Функция затрат представляет собой взвешенную сумму квадратов ошибок.
В зависимости от его аргументов, procest оценивает различные модели полиномов черного ящика. Вы можете использовать procest, например, для оценки параметров для линейных структур непрерывной временной передаточной функции, состояния-пространства или полиномиальной модели. Использовать procest, необходимо предоставить структуру модели с неизвестными параметрами и оценочными данными в качестве входных аргументов.
Для этой части учебного пособия необходимо определить структуру модели, как описано в разделе Определение структуры модели процесса. Использовать midproc0 в качестве структуры модели и Ze1 в качестве оценочных данных:
midproc = procest(Ze1,midproc0); present(midproc)
midproc =
Process model with 2 inputs: y = G11(s)u1 + G12(s)u2
From input "ConsumptionRate" to output "Production":
1+Tz*s
G11(s) = Kp * ---------------------- * exp(-Td*s)
1+2*Zeta*Tw*s+(Tw*s)^2
Kp = -1.1807 +/- 0.29987
Tw = 1.6437 +/- 714.6
Zeta = 16.036 +/- 6958.9
Td = 2.426 +/- 64.276
Tz = -109.19 +/- 63.738
From input "Current" to output "Production":
Kp
G12(s) = ---------- * exp(-Td*s)
1+Tp1*s
Kp = 10.264 +/- 0.048404
Tp1 = 2.049 +/- 0.054901
Td = 4.9175 +/- 0.034374
Parameterization:
{'P2DUZ'} {'P1D'}
Number of free coefficients: 8
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Termination condition: Maximum number of iterations reached..
Number of iterations: 20, Number of function evaluations: 279
Estimated using PROCEST on time domain data "Ze1".
Fit to estimation data: 86.2%
FPE: 6.081, MSE: 5.984
More information in model's "Report" property.
В отличие от моделей полиномов дискретного времени, модели непрерывного времени позволяют оценить задержки. В этом случае расчетные значения задержки отличаются от исходных предположений, указанных в 2.5 и 5 соответственно. Большие неопределенности в оценочных значениях параметров G_1(s) указывают, что динамика от ввода 1 к выходному сигналу не улавливаются должным образом.
Дополнительные сведения об оценке моделей см. в разделе Модели процессов.
В этой части учебного пособия создается график, на котором сравниваются фактические выходные данные и выходные данные модели.
compare(Zv1,midproc)

График показывает, что выход модели разумно согласуется с измеренным выходом: между моделью и данными проверки есть согласие в 60%.
Использовать resid для проведения остаточного анализа.
resid(Zv1,midproc)

Взаимная корреляция между вторыми входными и остаточными ошибками является значительной. График автокорреляции показывает значения вне доверительной области и показывает, что остатки коррелированы.
Измените алгоритм итеративной оценки параметров на Левенберг-Марквардт.
Opt = procestOptions;
Opt.SearchMethod = 'lm';
midproc1 = procest(Ze1,midproc,Opt);
Изменение свойств алгоритма или определение начальных предположений параметров и повторное выполнение оценки могут улучшить результаты моделирования. Добавление шумовой модели может улучшить результаты прогнозирования, но не обязательно результаты моделирования.
В этой части учебного пособия показано, как оценить модель процесса и включить модель шума в оценку. Включение шумовой модели обычно улучшает результаты прогнозирования модели, но не обязательно результаты моделирования.
Для задания шума ARMA первого порядка используются следующие команды:
Opt = procestOptions;
Opt.DisturbanceModel = 'ARMA1';
midproc2 = procest(Ze1,midproc0,Opt);
Можно ввести 'dist' вместо 'DisturbanceModel'. Имена свойств не чувствительны к регистру, и необходимо включить только ту часть имени, которая уникально идентифицирует свойство.
Сравните полученную модель с измеренными данными.
compare(Zv1,midproc2)

График показывает, что выходные данные модели поддерживают разумное согласие с выходными данными проверки.
Выполните остаточный анализ.
resid(Zv1,midproc2)

Остаточный график показывает, что значения автокорреляции находятся внутри доверительных границ. Таким образом, добавление шумовой модели приводит к образованию некоррелированных остатков. Это указывает на более точную модель.
В этой части учебного пособия оценивается несколько различных типов моделей полиномов «черный ящик» и «вход-выход».
Необходимо подготовить данные, как описано в разделе Подготовка данных.
Для задания порядка полиномиальной модели можно использовать следующие предыдущие результаты оценочных порядков модели.
Для первой комбинации ввода/вывода используйте:
Два полюса, соответствующие na = 2 в модели ARX.
Один ноль, соответствующий nb = 2 в модели ARX.
Задержка 5, соответствующая nk = 5 выборок (или 2,5 минут) в модели ARX.
Для второй комбинации ввода/вывода используйте:
Один полюс, соответствующий na = 1 в модели ARX.
Нулей нет, что соответствует nb = 1 в модели ARX.
Задержка 10, соответствующая nk = 10 выборок (или 5 минут) в модели ARX.
Сведения о моделях ARX. Для системы с одним входом/одним выходом (SISO) структура модели ARX:
(t − nk − nb + 1) + e (t)
y (t) представляет выходной сигнал в момент времени t, u (t) представляет входной сигнал в момент времени t, na - число полюсов, nb - число нулей плюс 1, nk - количество выборок до того, как входной сигнал повлияет на выходной сигнал системы (называемое задержкой или мертвым временем модели), и e (t) - возмущение белого шума.
Структура модели ARX не различает полюса для отдельных путей ввода/вывода: деление уравнения ARX на A, которое содержит полюса, показывает, что A появляется в знаменателе для обоих входов. Поэтому можно задать значение na для суммы полюсов для каждой пары вход/выход, которое равно 3 в данном случае.
Продукт System Identification Toolbox оценивает параметры an ... bn с использованием указанных данных и заказов моделей.
Оценка моделей ARX с использованием arx. Использовать arx для вычисления полиномиальных коэффициентов с использованием быстрого, неидертеративного метода arx:
marx = arx(Ze1,'na',3,'nb',[2 1],'nk',[5 10]); present(marx) % Displays model parameters % with uncertainty information
marx =
Discrete-time ARX model: A(z)y(t) = B(z)u(t) + e(t)
A(z) = 1 - 1.027 (+/- 0.02907) z^-1 + 0.1678 (+/- 0.042) z^-2 + 0.01289 (
+/- 0.02583) z^-3
B1(z) = 1.86 (+/- 0.189) z^-5 - 1.608 (+/- 0.1888) z^-6
B2(z) = 1.612 (+/- 0.07392) z^-10
Sample time: 0.5 minutes
Parameterization:
Polynomial orders: na=3 nb=[2 1] nk=[5 10]
Number of free coefficients: 6
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using ARX on time domain data "Ze1".
Fit to estimation data: 90.7% (prediction focus)
FPE: 2.768, MSE: 2.719
More information in model's "Report" property.
MATLAB оценивает многочлены A , B1 , и B2. Неопределенность для каждого из параметров модели вычисляется как 1 стандартное отклонение и появляется в скобках рядом с каждым значением параметра.
Кроме того, можно использовать следующий сокращенный синтаксис и указать порядки моделей в качестве одного вектора.
marx = arx(Ze1,[3 2 1 5 10]);
Доступ к данным модели. Модель, которую вы оценили, marx, является дискретным временем idpoly объект. Чтобы получить свойства этого объекта модели, можно использовать get функция:
get(marx)
A: [1 -1.0267 0.1678 0.0129]
B: {[0 0 0 0 0 1.8599 -1.6084] [0 0 0 0 0 0 0 0 0 0 1.6118]}
C: 1
D: 1
F: {[1] [1]}
IntegrateNoise: 0
Variable: 'z^-1'
IODelay: [0 0]
Structure: [1x1 pmodel.polynomial]
NoiseVariance: 2.7436
InputDelay: [2x1 double]
OutputDelay: 0
Ts: 0.5000
TimeUnit: 'minutes'
InputName: {2x1 cell}
InputUnit: {2x1 cell}
InputGroup: [1x1 struct]
OutputName: {'Production'}
OutputUnit: {'mg/min'}
OutputGroup: [1x1 struct]
Notes: [0x1 string]
UserData: []
Name: ''
SamplingGrid: [1x1 struct]
Report: [1x1 idresults.arx]
Доступ к информации, хранящейся в этих свойствах, можно получить с помощью точечной нотации. Например, можно вычислить дискретные полюса модели, найдя корни A полином.
marx_poles = roots(marx.a)
marx_poles =
0.7953
0.2877
-0.0564
В этом случае вы получаете доступ к A полином с использованием marx.a.
Модель marx описывает динамику системы с использованием трех дискретных полюсов.
Совет
Также можно использовать pole для непосредственного вычисления полюсов модели.
Подробнее. Дополнительные сведения об оценке полиномиальных моделей см. в разделе Полиномиальные модели ввода-вывода.
Дополнительные сведения о доступе к данным модели см. в разделе Извлечение данных.
Сведения о моделях пространства состояния. Общая структура модели «состояние-пространство»:
(t) + Du (t) + e (t)
y (t) представляет выходной сигнал в момент времени t, u (t) представляет входной сигнал в момент времени t, x (t) является вектором состояния в момент времени t, и e (t) является возмущением белого шума.
Для оценки модели «состояние-пространство» необходимо указать одно целое число в качестве порядка модели (размерность вектора состояния). По умолчанию задержка равна 1.
Продукт System Identification Toolbox оценивает матрицы состояния-пространства A, B, C, D и K с использованием порядка модели и заданных данных.
Структура модели state-space является хорошим выбором для быстрой оценки, поскольку она содержит только два параметра: n - количество полюсов (размер матрицы A) и nk - задержка.
Оценка моделей состояния-пространства с использованием n4sid. Используйте n4sid команда для задания диапазона порядков моделей и оценки производительности нескольких моделей пространства состояний (порядки от 2 до 8):
mn4sid = n4sid(Ze1,2:8,'InputDelay',[4 9]);Эта команда использует метод fast, noniterative (подпространство) и открывает следующий график. Этот график используется для определения состояний, обеспечивающих значительный относительный вклад в поведение ввода/вывода, и состояний, обеспечивающих наименьший вклад.
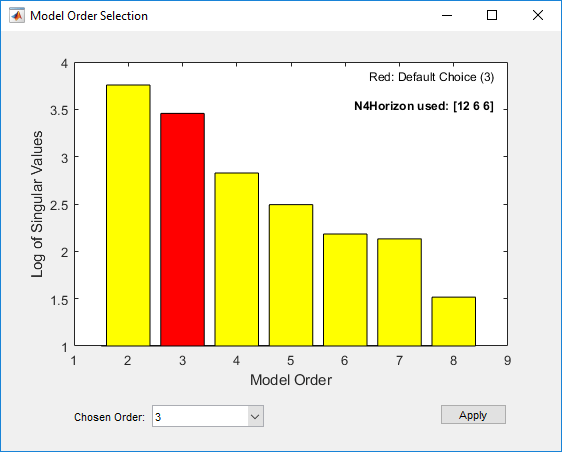
Вертикальная ось является относительной мерой того, насколько каждое состояние вносит вклад в поведение ввода/вывода модели (журнал сингулярных значений ковариационной матрицы). Горизонтальная ось соответствует порядку модели n. Этот график рекомендует n=3, обозначается красным прямоугольником.
В поле Выбранный заказ отображается рекомендуемый заказ модели. 3 в этом случае по умолчанию. Выбор заказа можно изменить с помощью раскрывающегося списка Выбранный заказ. Примените значение в поле Выбранный заказ и закройте окно выбора заказа, щелкнув Применить.
По умолчанию n4sid использует свободную параметризацию формы state-space. Чтобы оценить каноническую форму, установите значение SSParameterization свойство для 'Canonical' . Можно также указать задержку ввода-вывода (в выборках) с помощью 'InputDelay' собственность.
mCanonical = n4sid(Ze1,3,'SSParameterization','canonical','InputDelay',[4 9]); present(mCanonical); % Display model properties
mCanonical =
Discrete-time identified state-space model:
x(t+Ts) = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2 x3
x1 0 1 0
x2 0 0 1
x3 0.0737 +/- 0.05919 -0.6093 +/- 0.1626 1.446 +/- 0.1287
B =
ConsumptionR Current
x1 1.844 +/- 0.175 0.5633 +/- 0.122
x2 1.063 +/- 0.1673 2.308 +/- 0.1222
x3 0.2779 +/- 0.09615 1.878 +/- 0.1058
C =
x1 x2 x3
Production 1 0 0
D =
ConsumptionR Current
Production 0 0
K =
Production
x1 0.8674 +/- 0.03169
x2 0.6849 +/- 0.04145
x3 0.5105 +/- 0.04352
Input delays (sampling periods): 4 9
Sample time: 0.5 minutes
Parameterization:
CANONICAL form with indices: 3.
Feedthrough: none
Disturbance component: estimate
Number of free coefficients: 12
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using N4SID on time domain data "Ze1".
Fit to estimation data: 91.39% (prediction focus)
FPE: 2.402, MSE: 2.331
More information in model's "Report" property.
Примечание
mn4sid и mCanonical представляют собой дискретно-временные модели. Чтобы оценить модель непрерывного времени, установите 'Ts' свойство для 0 в команде оценки или используйте ssest команда:
mCT1 = n4sid(Ze1, 3, 'Ts', 0, 'InputDelay', [2.5 5]) mCT2 = ssest(Ze1, 3,'InputDelay', [2.5 5])
Подробнее. Дополнительные сведения об оценке моделей пространства состояний см. в разделе Модели пространства состояний.
Сведения о моделях Бокса (Box) - Дженкинса (Jenkins Models). Общая структура Бокса-Дженкинса (BJ):
(q) D (q) e (t)
Чтобы оценить модель BJ, необходимо указать параметры nb, nf, nc, nd и nk.
В то время как структура модели ARX не различает полюса для отдельных путей ввода/вывода, модель BJ обеспечивает большую гибкость при моделировании полюсов и нулей возмущения отдельно от полюсов и нулей динамики системы.
Оценка модели BJ с использованием полиэфира. Вы можете использовать polyest для оценки модели BJ. polyest является итеративным методом и имеет следующий общий синтаксис:
polyest(data,[na nb nc nd nf nk]);
Для оценки модели BJ введите:
na = 0; nb = [ 2 1 ]; nc = 1; nd = 1; nf = [ 2 1 ]; nk = [ 5 10]; mbj = polyest(Ze1,[na nb nc nd nf nk]);
Эта команда определяет nf=2 , nb=2 , nk=5 для первого входа, и nf=nb=1 и nk=10 для второго входа.
Отображение информации о модели.
present(mbj)
mbj =
Discrete-time BJ model: y(t) = [B(z)/F(z)]u(t) + [C(z)/D(z)]e(t)
B1(z) = 1.823 (+/- 0.1792) z^-5 - 1.315 (+/- 0.2367) z^-6
B2(z) = 1.791 (+/- 0.06431) z^-10
C(z) = 1 + 0.1068 (+/- 0.04009) z^-1
D(z) = 1 - 0.7452 (+/- 0.02694) z^-1
F1(z) = 1 - 1.321 (+/- 0.06936) z^-1 + 0.5911 (+/- 0.05514) z^-2
F2(z) = 1 - 0.8314 (+/- 0.006441) z^-1
Sample time: 0.5 minutes
Parameterization:
Polynomial orders: nb=[2 1] nc=1 nd=1 nf=[2 1]
nk=[5 10]
Number of free coefficients: 8
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Termination condition: Near (local) minimum, (norm(g) < tol)..
Number of iterations: 6, Number of function evaluations: 13
Estimated using POLYEST on time domain data "Ze1".
Fit to estimation data: 90.75% (prediction focus)
FPE: 2.733, MSE: 2.689
More information in model's "Report" property.
Неопределенность для каждого из параметров модели вычисляется как 1 стандартное отклонение и появляется в скобках рядом с каждым значением параметра.
Полиномиалы C и D дать числитель и знаменатель шумовой модели соответственно.
Совет
Кроме того, можно использовать следующий сокращенный синтаксис, указывающий порядки как один вектор:
mbj = bj(Ze1,[2 1 1 1 2 1 5 10]);
bj является версией polyest это конкретно оценивает структуру модели BJ.
Подробнее. Дополнительные сведения об идентификации полиномиальных моделей ввода-вывода, таких как BJ, см. в разделе Полиномиальные модели ввода-вывода.
Сравните выходные данные моделей ARX, state-space и Box-Jenkins с измеренными выходными данными.
compare(Zv1,marx,mn4sid,mbj)

compare строит график измеренных выходных данных в наборе проверочных данных относительно моделируемых выходных данных моделей. Входные данные из набора данных проверки служат в качестве входных данных для моделей.
Выполните остаточный анализ моделей ARX, state-space и Box-Jenkins.
resid(Zv1,marx,mn4sid,mbj)

Все три модели одинаково хорошо моделируют выходные данные и имеют некоррелированные остатки. Поэтому выберите модель ARX, поскольку она является простейшей из трех полиномиальных моделей ввода-вывода и адекватно фиксирует динамику процесса.
В этой части учебного пособия выполняется моделирование выходных данных модели. Необходимо создать модель непрерывного времени. midproc2, как описано в разделе Оценка моделей процессов.
Для моделирования выходных данных модели требуется следующая информация:
Входные значения для модели
Начальные условия для моделирования (также называемые начальными состояниями)
Например, следующие команды используют iddata и idinput команды для построения набора входных данных и использования sim для моделирования выходных данных модели:
% Create input for simulation U = iddata([],idinput([200 2]),'Ts',0.5,'TimeUnit','min'); % Simulate the response setting initial conditions equal to zero ysim_1 = sim(midproc2,U);
Чтобы максимизировать соответствие между моделируемым откликом модели на измеренный выходной сигнал для одного и того же входного сигнала, можно вычислить начальные условия, соответствующие измеренным данным. Наилучшие подходящие начальные условия могут быть получены с помощью findstates в версии состояния-пространства расчетной модели. Следующие команды оценивают начальные состояния X0est из набора данных Zv1:
% State-space version of the model needed for computing initial states
midproc2_ss = idss(midproc2);
X0est = findstates(midproc2_ss,Zv1);
Затем смоделируйте модель, используя начальные состояния, оцененные на основе данных.
% Simulation input Usim = Zv1(:,[],:); Opt = simOptions('InitialCondition',X0est); ysim_2 = sim(midproc2_ss,Usim,Opt);
Сравните смоделированные и измеренные выходные данные на графике.
figure
plot([ysim_2.y, Zv1.y])
legend({'model output','measured'})
xlabel('time'), ylabel('Output')

Многие приложения для проектирования систем управления требуют прогнозирования будущих выходов динамической системы с использованием прошлых входных/выходных данных.
Например, использовать predict для прогнозирования реакции модели на пять шагов вперед:
predict(midproc2,Ze1,5)

Сравните прогнозируемые выходные значения с измеренными выходными значениями. Третий аргумент compare задает пятишаговое прогнозирование. Если третий аргумент не указан, compare предполагает бесконечный горизонт прогнозирования и имитирует выходные данные модели.
compare(Ze1,midproc2,5)

Использовать pe для вычисления ошибки прогнозирования Err между прогнозируемыми выходами midproc2 и измеренный выходной сигнал. Затем постройте график спектра ошибок с помощью spectrum команда.
[Err] = pe(midproc2,Zv1); spectrum(spa(Err,[],logspace(-2,2,200)))

Ошибки прогнозирования строятся с доверительным интервалом 1 стандартного отклонения. Погрешности выше на высоких частотах из-за высокочастотного характера возмущения.