Документация

Смещенные оценки

Если выборки игнорируются, количество выборок, используемых в оценке, меньше NumSamples. Очевидно, что фактического количества используемых выборок должно быть достаточно для получения оценок. В сложение, хотя параметры модели Parameters (или средние оценки Mean) являются объективными максимальными оценками правдоподобия, остаточной ковариационной оценкой Covariance смещен. Чтобы преобразовать в объективную ковариационную оценку, умножите Covariance около

где Count - фактическое количество выборок, используемых в оценке с Count ≤ NumSamples. Ни одна из регрессионных функций не выполняет эту настройку.

Требования

Регрессионные функции, особенно функции оценки, имеют несколько требований. Во-первых, они должны иметь допустимые значения для NumSamples, NumSeries, и NumParams. Как правило, многомерные нормальные регрессионые функции

и регрессионные функции методом наименьших квадратов требуют

где Count - фактическое количество выборок, используемых в оценке с

Во-вторых, они должны иметь достаточно несовпадающих значений, чтобы сходиться. В-третьих, у них должна быть неотрицательная ковариационная матрица.

Хотя в ссылках можно найти некоторые необходимые и достаточные условия, общих условий существования и уникальности решений в случае недостающих данных не существует. Неконвергенция обычно происходит из-за плохо обусловленной ковариации матрицы, которая более подробно обсуждается в Nonconvergence.

Медленная сходимость

Поскольку сходимость алгоритма ECM в худшем случае линейна, можно выполнить сотни и даже тысячи итераций перед завершением алгоритма. Если вы регулярно оцениваете с помощью алгоритма ECM с регулярными обновлениями, можно использовать предыдущие оценки в качестве начальных догадок для оценки следующего периода. Этот подход часто ускоряет вещи, поскольку инициализация по умолчанию в регрессионых функциях устанавливает начальные параметры b в нуль и начальное ковариационное C быть матрицей тождеств.

Другие импровизированные подходы возможны, хотя большинство подходов зависят от проблем. В частности, для средней и ковариационной оценки, функция оценки ecmnmle использует функцию ecmninit для получения начальной оценки.

НеРандомные невязки

Одновременные оценки параметров b и ковариации C требовать C быть положительно-определенным. Таким образом, общая многомерная нормальная регрессия стандартных программ требовать неотрицательных остаточных ошибок. Если вы столкнулись с моделью, которая имеет точные результаты, стандартная программа наименьших квадратов ecmlsrmle все еще работает, хотя и обеспечивает оценку методом наименьших квадратов с сингулярной остаточной ковариационной матрицей. Другие функции регрессии не выполняются.

Несходимость

Хотя регрессионные функции устойчивы и работают в большинстве «типичных» случаев, они могут не сходиться. Основной тип отказа является плохо обусловленной ковариационной матрицей, где отказы являются либо мягкими, либо жесткими. Мягкий отказ бесконечно блуждает к почти сингулярной ковариационной матрице и может быть замечена, если алгоритм не сходится после примерно 100 итераций. Если MaxIterations увеличивается до 500 и запускается режим отображения (без выходных аргументов), типичный мягкий отказ выглядит следующим образом.

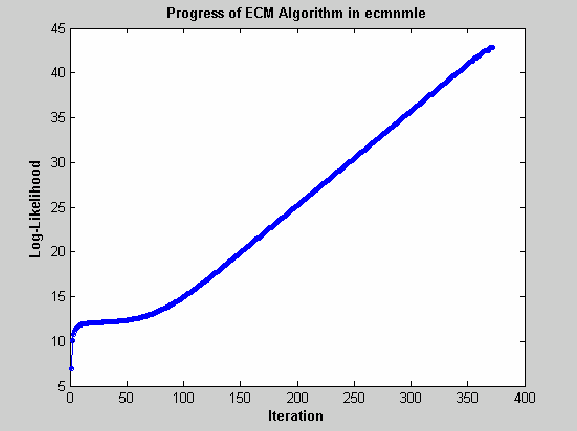
Этот случай, который основан на 20 наблюдениях пяти активов с 30% отсутствующих данных, показывает, что логарифмическая правдоподобность переходит линейно к бесконечности, когда функция правдоподобия переходит к 0. В этом случае функция сходится, но ковариационная матрица эффективно сингулярна с наименьшим собственным значением в порядке точности машины (eps).

Для функции ecmnmle, жесткая ошибка выглядит следующим образом:

> In ecmninit at 60
  In ecmnmle at 140
??? Error using ==> ecmnmle
Full covariance not positive-definite in iteration 218.

С практической точки зрения, если есть сомнения, проверьте свою остаточную ковариационную матрицу из стандартных программ, чтобы убедиться, что она положительно-определена. Это важно, потому что мягкая ошибка имеет матрицу, которая, по-видимому, положительно-определена, но на самом деле имеет почти нуль ценное собственное значение в пределах точности машины. Для этого с ковариация оценки Covariance, использовать cond(Covariance), где любое значение, больше 1/eps следует считать подозрительным.

Однако, если происходит любой тип отказа, обратите внимание, что стандартная программа регрессии указывает, что с данными, вероятно, что-то не так. (Даже без отсутствующих данных, два временных рядов, которые пропорциональны друг другу, создают сингулярную ковариационную матрицу.)